直線の像，領域の像

← PC用は別頁

== 直線の像，領域の像 ==

【１次変換の線形性】
　１次変換fは，次の関係を満たします．これを１次変換の線形性といいます．

（２つのベクトルの和を１次変換したものは，各々のベクトルを１次変換してから和を求めたものに等しい
⇔１次変換とベクトルの和は順序を入れ替えることができる）

(1)　f(+)=f()+f()

（ベクトルの定数倍を１次変換したものは，ベクトルを１次変換してから定数倍したものに等しい
⇔１次変換とベクトルの定数倍は順序を入れ替えることができる）

(2)　f()=kf()

以上の(1)(2)から，一般に，a, bを定数とするとき
(*) f(a+b)=af()+bf()
が成り立ちます．

（解説）
　２次元ベクトルを次のような２×１行列（列ベクトル）で表します．

　１次変換fが行列によって表されるとき，

　１次変換f()は，次のような行列の積に対応します．

.f()=

(1)←
　行列の積については，次の分配法則が成り立ちます．

.=+

したがって
.f(+)=f()+f()
が成り立ちます．
(2)←
　行列の積について，次の等式が成り立ちます．

.k=k

したがって
.f()=kf()
が成り立ちます．

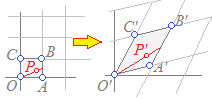
※　上記の線形性により，図形の１次変換について，次の性質が成り立ちます．

ここでは，逆行列が存在する（D=ad−bc≠0，正則）１次変換について述べる．逆行列が存在しない（D=ad−bc=0，正則でない）１次変換では，平面全体が直線や点に「つぶれる」場合があり，ここではこれを考えない．逆行列が存在する１次変換では，平面全体は平面全体に１対１に対応します．

(A)　直線は直線に移される

真っ直ぐなものが，１次変換によって曲がることはない．

（解説）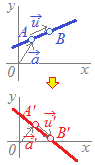

　点A()を通り方向ベクトル=に平行な直線は，ベクトル方程式
.=+t
（tは実数）
で表される．
位置ベクトルP(), 点A()，方向ベクトル=→ABの１次変換fによる像を各々’=f()，A’()，=→A'B'とすると
.f()=f(+t)=f()+f(t)
.=’+t’
ゆえに
.’=’+t’
これは，P'(’)が点A'(’)を通り，方向ベクトル’=→A'B'に平行な直線上にあることを示している．

(B)　線分の内分比は変わらない

元の内分比がPQ:QR=m:nのとき，P'Q':Q'R'もm:nになる．

（解説）

点Q()が２点P(), R()をm:nに内分するとき

　点P(), Q(), R()の１次変換fによる像を各々
P'()=f(), Q'()=f(), R'()=f()とすると

.f() =f

ゆえに

これは，点Q'()が２点P'(), R'()をm:nに内分することを示している．

※　逆行列が存在する（D=ad−bc≠0，正則）１次変換については，この他に，つぎのような性質も成り立ちます．
　しかし，直線や領域の移動を考えるときに，真っ先に利用できるのは上の２つの性質です．

*** 逆行列が存在するときの直線の像 ***

【例１】

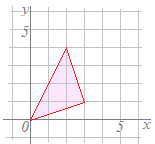
　１次変換=によって，直線y=3x

がどのような図形に移されるか調べてください．

（解答）　（２点の像で求める方法）

図形y=3xの変換となると考えにくいという場合には，点の移動で求める．
選ぶのは直線上の２点ならどれでもよいが，性質(A)により「直線は直線に移される」ことが分かっているから，出てきた２点を結ぶ直線の方程式を求めると答が出る．

　原点Oは

.==によって

原点O' に移される．

　次に，直線y=3x上の１つの点Pは

.==によって

点P' に移される．

　(A) により直線は直線に移されるから，直線OPは直線O'P'に移される．
　O'P'の方程式はy=x …（答）

（別解１）　（逆変換による方法）

　旧座標(x, y)の関係式が
.y=3x…(1)
　新旧の関係式が

　= …(2)

であるときに，新座標(x', y')の関係式を求めたらよい．
(2)を変形して

　=−1=

したがって

　…(2')

(2')を(1)に代入

(x'+y')=3(x'−y')

(x'+2y')=3(4x'−3y')
11y'=11x'
y'=x'
通常の表記に直すと
y=x …（答）

（別解２）　（媒介変数表示による方法）

　方程式y=3x…(1) のままでは

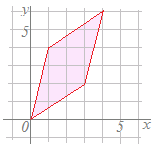
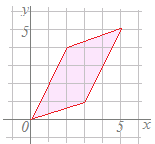
　= …(2)

に代入することはできませんが，これを媒介変数表示に直してx座標とx座標に分けると，代入できるようになります

(1)式を媒介変数表示に直してx=t, y=3t…(1')とする
(1')を(2)に代入すると

　x'=11t , y'=11tから媒介変数tを消去すると
　y'=x'
通常の表記戻すと
　y=x …（答）

（別解３）　（図で考える方法）

　１次変換=によって

　=は=に移され

　=は=に移されます．

　このとき点=x+y=x+yは

　x+y

　=x+y=x+y

　=x+yに移されますので，次図のピンク色はピンク色の部分に，緑色は緑色，水色は水色に各々移されます．
　そこで上の図の赤で示した直線y=3xは下の図の赤で示した直線に移されます．

目の子算（めのこざん）という言葉があるらしい．･･･まともに計算せずに，目で見て合わせる方法

丸印の所などを参考にすると，y=x…（答）

※　上の【例１】のように，原点を通る直線の像を求めたいとき，原点の像は必ず原点になるから，他にもう一つの点の像を求めて，２点の像を求めるとよい．
　次のようにまとめることができます．

直線の像の求め方（その１）

⇒　直線の像は，２点の像で求められます

２点の像が得られたら，それら２点(a, b) , (c, d)を通る直線の方程式は，次の公式で求められます．
○　c≠aのとき

.y−b=(x−a)

○　c=aのときは
　次図のようにx軸に垂直な直線になるから
.x=a　（またはx=c）

　上の【例１】では，２点(0, 0) , (11, 11)を通る直線の方程式として

.y−0=(x−0)

で求めています．

直線の像の求め方（その２）

　⇒　逆変換を使えば，x, yの関係式をx', y'の関係式に直せます．

は，逆行列A−1を求めたら

　=A−1

と書き直せます．

直線の像の求め方（その３）

　⇒　媒介変数表示を使えば，方程式y=f(x)の代わりに点の座標( ...t, ...t)になるので，そのまま変換式に代入できます．

【媒介変数表示に直すには】
○　関数y=f(x)の形で書かれている方程式を媒介変数表示直すには，

x=t, y=f(t) （tは媒介変数）とするとよい

例えば，y=2x+1を媒介変数表示に直すには

x=t, y=2t+1 （tは媒介変数）とするとよい

○　y=...の形に変形しにくい場合，例えば，x=y2+1の場合ならば

y=t, x=t2+1 （tは媒介変数）とするとよい

※　媒介変数表示に直す方法は１つではないので，例えば2x+3y+1=0の場合ならば

(1) x=t, y=−t− （tは媒介変数）でもよく

(2) y=s, x=−s− （sは媒介変数）でもよい

(3) 2(x−1)=−3(y+1)と変形して
x−1=3u, y+1=−2u
⇔ x=3u+1, y=−2u−1（uは媒介変数）でもよい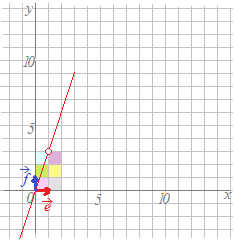

【問題１】

で表される１次変換によって，直線x+3y=1がどのような図形に移されるか調べてください．

やり直す HELP1 HELP2 HELP3 解答を見る

. 2x−4y=−1 . y=−2x+1

. 4x−2y=1 . y=2x−1

（２点の像で求める方法）
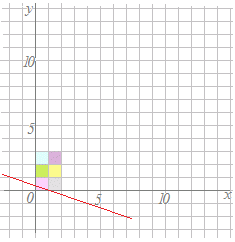
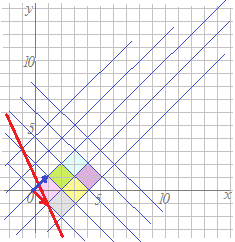
(1)　直線x+3y=1の上にある２点を選びます．例えば(1, 0), (−2, 1)を選びます．
(2)　これら２点の像を各々求めます．

(3) 像となる２点の座標(1, −1), (−1, 3)から，２点を通る直線の方程式を求めます．

.y+1=(x−1)

.y+1=−2(x−1)

（逆変換による方法）
逆行列を求めて(x, y)を(x', y')で表します．

　=−1=

したがって

　…(*)

(*)をx+3y=1に代入

(x'−y')+3(x'+y')=1

x'−y'+3x'+3y'=2
4x'+2y'=2
2x'+y'=1

（媒介変数表示による方法）
x+3y=1を媒介変数表示に直してx=1−3t, y=t…(*)とする

なぜ，媒介変数表示としてx=t, y=...にしないのか？
それでもよろしいが，分数計算になると暑苦しいので逃げたのです．

(*)を代入すると

　x'=1−2t , y'=−1+4tから媒介変数tを消去する
.2t=1−x'をy'=−1+4tに代入すると
.y'=−1+2(1−x')=−2x'+1

.y=−2x+1になります．

【問題２】

で表される１次変換によって，直線x+2y=4がどのような図形に移されるか調べてください．

やり直す HELP1 HELP2 HELP3 解答を見る

. 3x−2y+4=0 . 3x−2y−2=0

. 13x+10y−4=0 . 13x−10y+4=0

（２点の像で求める方法）
(1)　直線x+2y=4の上にある２点を選びます．例えば(0, 2), (4, 0)を選びます．
(2)　これら２点の像を各々求めます．

(3) 像となる２点の座標(4, 8), (12, 20)から，２点を通る直線の方程式を求めます．

.y−8=(x−4)

（逆変換による方法）
逆行列を求めて(x, y)を(x', y')で表します．

　=−1=

したがって

　…(*)

(*)をx+2y=4に代入

(2x'−y')+(−5x'+3y')=4

−3x'+2y'=4

（媒介変数表示による方法）
x+2y=4を媒介変数表示に直してx=4−2t, y=t…(*)とする
(*)を代入すると

　x'=12−4t , y'=20−6tから媒介変数tを消去する
.3x'−2y'=−4

.3x−2y+4=0になります．

*** 逆行列が存在するときの多角形の像 ***

【例２】

　１次変換=によって，

領域{ (x, y) | 0≦x≦1, 0≦y≦1 }がどのような図形に移されるか調べてください．

（解答）
　頂点O(0, 0), A(1, 0), B(1, 1), C(0, 1)はこの１次変換によって各々

.= …O'

.= …A'

.= …B'

.= …C'

に移される．
　このとき，四角形OABCは四角形O'A'B'C'に移され，四角形OABCの内部は四角形O'A'B'C'の内部に移されます．
　したがって，O'(0, 0), A'(5, 2), B'(8, 3), C'(3, 1)を頂点とする四角形の内部および周上 …（答）

　直線は直線に移されるから，線分OAは線分O'A'に移され，他の３つの辺も同様　⇒　四角形の周上の点は周上の点に移される．
　次に，図のような四角形の内部の点Pは，「内分比が変わらない」ことにより，内分比が同じ図のような点P'に移されるので，四角形の内部の点は新しい四角形の内部の点に移されます．

　このようにして，

図形の周辺の像を求めれば図形の像は求められます．
特に，三角形，四角形のような直線で囲まれた図形の像は，頂点の像を求めるだけで求められます．

【問題３】

で表される１次変換によって，３点O(0, 0), A(1, 0), B(0, 1)を頂点とする三角形OABの内部および周上がどのような図形に移されるか調べてください．

HELP

　頂点O(0, 0), A(1, 0), C(0, 1)はこの１次変換によって各々

.= …O'

.= …A'

.= …B'

に移される．
　このとき，三角形OABは三角形O'A'B'に移され，三角形OABの内部は三角形O'A'B'の内部に移されます．
　したがって，O'(0, 0), A'(3, 2), B'(1, 4)を頂点とする三角形の内部および周上 …（答）

【問題４】

　=で表される１次変換によって，

領域{ (x, y) | 0≦x≦1, 0≦y≦1 }がどのような図形に移されるか調べてください．

HELP

　頂点O(0, 0), A(1, 0), B(1, 1), C(0, 1)はこの１次変換によって各々

.= …O'

.= …A'

.= …B'

.= …C'

に移される．
　このとき，四角形OABCは四角形O'A'B'C'に移され，四角形OABCの内部は四角形O'A'B'C'の内部に移されます．
　したがって，O'(0, 0), A'(2, −1), B'(2, 3), C'(0, 4)を頂点とする四角形の内部および周上 …（答）

*** １次変換による原像 ***

【例３】

　１次変換=によって，

直線y=3x+1に移される元の図形を求めてください．

（解答）
　新座標(x', y')の関係式
.y'=3x'+1…(1)
と，新座標(x', y')と旧座標(x, y)の変換式

.= ⇔ …(2)

から新座標(x', y')を消去して，旧座標(x, y)の関係式を作ればよい．
　(2)を(1)に代入すると
.4x+2y=3(3x−y)+1
.5x−5y+1=0…（答）

　像の関係式（新座標の方程式）y'=3x'+1から原像の関係式y=...x+...を求める手続きを理屈で考えれば逆変換に見えますが，上欄のように(x', y')と(x, y)の関係を整理すると，『意外な事に』元の１次変換のまま使えばよいことが分かります．

※　この問題では，直線y=3x+1上の２点，例えば(0, 1), (1, 4)の原像を求めて，それら２点を通る直線の方程式を計算する方法も考えられますが，「逆行列の計算」「２点の原像の計算」「２点を通る直線の方程式の計算」と長い道のりになり，大変です．

【問題５】
　１次変換=によって，

直線2x+3y−1=0に移される元の図形を求めてください．やり直す HELP 解答を見る

. 2x+7y−1=0 . 7x−2y−1=0

. 11x+13y−17=0 . 17x+13y−11=0

　新座標(x', y')の関係式
.2x'+3y'−1=0…(1)
と，新座標(x', y')と旧座標(x, y)の変換式

.= ⇔ …(2)

から新座標(x', y')を消去して，旧座標(x, y)の関係式を作ればよい．

　(2)を(1)に代入すると
.2(−x+5y)+3(3x−4y)−1=0
.7x−2y−1=0になります（答）

【問題６】
　１次変換=によって，

直線y=−2xに移される元の図形を求めてください．やり直す HELP 解答を見る

. y=2x . y=−2x

. x=2y . x=−2y

　新座標(x', y')の関係式
.y'=−2x'…(1)
と，新座標(x', y')と旧座標(x, y)の変換式

.= ⇔ …(2)

から新座標(x', y')を消去して，旧座標(x, y)の関係式を作ればよい．

　(2)を(1)に代入すると
.(−2x+3y)=−2(2x−y)
.y=−2xになります（答）
※この問題では，直線y=−2xは直線y'=−2x'に移され，原像と像が一致します．（ただし，原点以外の直線上の個々の点は移動しますが，直線全体の像が直線全体になるということです．）

*** 逆行列が存在するときの曲線図形の像 ***

【例４】

　１次変換=によって，

円x2+y2=1はどのような図形に移されますか．

　この問題は，元の図形が直線で囲まれた図形ではなく，曲線なので２点の像を直線でつないでも解答は得られません．
　しかし，単位面積{ (x, y) | 0≦x≦1, 0≦y≦1 }の像は略図を描くときには非常に参考になります．（次図参考）

（解答）
　旧座標(x, y)の関係式
.x2+y2=1…(1)
と，新座標(x', y')と旧座標(x, y)の変換式

. ⇔ =−1=

. ⇔ …(2)

から旧座標(x, y)を消去して，新座標(x', y')の関係式を作ればよい．
　(2)を(1)に代入すると

.(x'+y')2+(−x'+y'')2=1

....
.x'2+y'2=2
x, yの表記に直すと
.x2+y2=2…（答）

※　理屈で考えると，(x, y)の関係式を変換すると(x', y')の関係式になるように思われますが，実際の計算は，上の解説のように逆変換を代入します．
　したがって，この方法で答えられるのは，１次変換に逆行列が存在する場合だけです．

※　この問題は，元の図形が曲線なので，２点の像で直線の像を求める方法で解くことはできませんが，
単位面積{ (x, y) | 0≦x≦1, 0≦y≦1 }
の像を描くと平面が移される様子が視覚的に理解できます．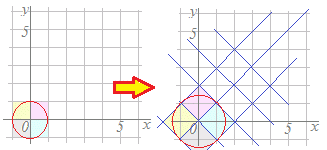

(0, 0)→(0, 0), (1, 0)→(1, 1), (1, 1)→(0, 2), (0, 1)→(−1, 1)だからピンクの四角形はピンクの四角形に移されます．同様にして，黄色は黄色へ，灰色は灰色へ，水色は水色へ移されます．
　この頁の先頭で述べた(B)の性質により，各々の色の中にある図形は各々の色の中に移されるので，赤で示した線は赤で示した線に移されます．（金網を引きのばして回転させた感じ）
　求めた線が円であることは，上のような計算によらなければ断定できません．

【問題７】
　１次変換=によって，

放物線y=x2はどのような図形に移されますか．やり直す HELP 解答を見る