|
=== 読者が配色を変更したい場合 ===
◎外側の色を変えるには，次の色をクリック
このページのバックアップ・ページ
（グーグルブロガー版）は，こちら⇒ ■ 「この部屋にいる生徒は，全員女子である」という命題が間違っていることを示すためには「この部屋にいるのは，全員男子である」ことを示す必要はなく，「男子が一人いる」ことを言えばよい． このように「全部が〜である」という判断が正しいのは，本当に「全部が〜である」ときだけで，１つでもそうでない例が見つかればこの命題は間違いであることになります． ■ 「ｐ→ｑ」 あるいは 「すべてのｘについて（ｐ（ｘ）→ｑ（ｘ））」は，集合ではＰ⊂Ｑに対応しており，「Ｐに含まれるどの要素もＱに含まれる」ことを主張しています．だから，Ｐのどの要素もＱに含まれていればこの命題は真ですが，Ｐの要素のうち１つでもＱに含まれないものがあれば，この命題は偽となります． ■ このように，ｐ→ｑという命題が間違っていることを示すには，ｐであってｑでない例を１つ示せばよいことになります． ｐ→ｑという命題が間違っていることを示すような例を，ｐ→ｑの反例といいます．（ｐ→ｑが真なら反例はありません．） 集合で言えば，Ｐ⊂Ｑの反例は，Ｐの要素であってＱの要素でないものです．
《要点》
例１
命題 ｐ→ｑ が間違っているとき，これが間違っていることを証明するには，ｐであってｑでない例を一つ示せばよい．このような例をｐ→ｑの反例といいます． Ｐ⊂Ｑが間違っていることを示すには，Ｐの要素であってＱの要素でないものを示します．このような例をＰ⊂Ｑの反例といいます．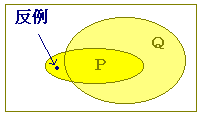 
反例１つで成立しないことの証明になります． ｘ＋ｙ＞０ → ｘ＞０かつｙ＞０ の反例：ｘ＝２，ｙ＝−１ 例２ ｘ２が整数ならばｘは整数 の反例：ｘ＝√2 例３ ａｂ＝ａｃ → ｂ＝ｃ の反例：ａ＝０，ｂ＝１，ｃ＝２ |
|
《問題》
次の命題は偽の命題です．次のうちこの命題の反例として適当なものを選びなさい．（各変数は実数とします） |
| １
ｘ＞１ ならば ｘ＞２ |
|
 |
| ２
ｘ＜１ ならば ｘ２＜１ |
|
|
| ３
ｘが４の倍数でないなら，ｘ２は４の倍数でない |
|
|
| ４
ｘ＋ｙ＞４ ならば ｘ＞２かつｙ＞２ |
|
|
| ５
ａ２＞ｂ２ならばａ＞ｂ |
|
|
| 《問題》 次の命題が間違っていることを示す反例を１つ示しなさい． |