== 円周角の定理 ==
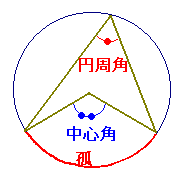
【円周角の定理】
一つの弧に対する「円周角」の大きさは，「中心角」の半分になります．
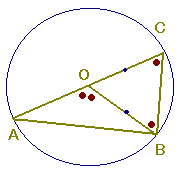（証明）
１ 右のようにＡＣが中心を通るとき
OC=OB=（半径）だから△ＯＢＣは二等辺三角形になる．
二等辺三角形の２つの底角は等しいから∠B=∠C…(1)
「三角形の外角は，それと隣り合わない２つの内角の和に等しい」（重要定理）から，
△OBCにおいて∠BOCの外角∠BOAは残り２つの角の和∠B+∠Cに等しいから
∠BOA=∠B+∠C…(2)
⇒ (1)(2)より∠BOA=2×∠C
すなわち「中心角は円周角の２倍になる」
「円周角は中心角の半分になる」
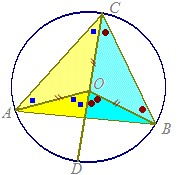２ 右図のように∠ACBの中に円の中心があるとき
AO=CO(=半径)だから△AOCは二等辺三角形になり
∠ACO=∠CAO
∠AOD=∠ACO+∠CAO
=2×∠ACO
同様にして
∠BOD=2×∠BCO
だから，両辺をそれぞれ足すと
∠AOB=2×∠ACO+2×∠BCO
=2×(∠ACO+∠BCO)
=2×∠ACB
すなわち「中心角は円周角の２倍になる」
「円周角は中心角の半分になる」
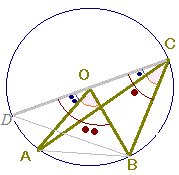３ 右の図のように∠ACBの外に円の中心があるとき
差で示します．
∠BOD=2×∠BCO
∠AOD=2×∠ACO
だから，両辺をそれぞれ引くと
∠BOA=2×∠BCO−2×∠ACO
=2×(∠BCO−∠ACO)
=2×∠BCA
すなわち「中心角は円周角の２倍になる」
「円周角は中心角の半分になる」
|
【具体例】
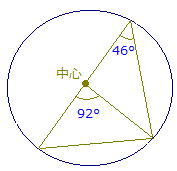
右図は左の証明で１の場合の例です
中心角92°が書いてあって，円周角が書いてないときは，92°÷2= 46°で円周角が求まります．
円周角46°が書いてあって，中心角が書いてないときは，46°×2= 92°で中心角が求まります．
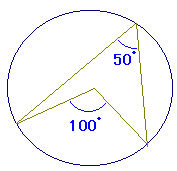
右図は左の証明で２の場合の例です
この場合も，中心角と円周角のいずれか一方が分かれば他方が求まります．
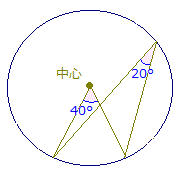
右図は左の証明で３の場合の例です
この場合にも円周角の定理が成り立ちます．
「中心角と円周角の対応」が，すぐに分かるように，目を慣らしておくことが大切です．
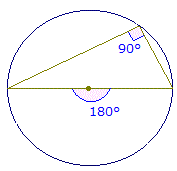◎右図のように中心角が180°のとき（中心を通る直線になるとき，すなわち直径になるとき）は特に重要です．
○直径は180°という角度になるということをしっかりと覚えましょう．
○また
「直径の上に立つ円周角は直角になる」
は重要定理ですからすぐに使えるように覚えておきましょう．
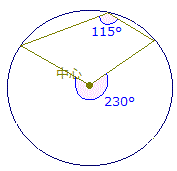
◎右図のように中心角が180°以上の場合に，「どこが中心角なのか」目の錯角で戸惑うことがありますので，幾つか見て慣れておくことが大切です．
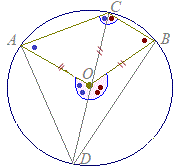この場合でも，「中心角=2×円周角」は，同様にして証明できます．
AO=CO(=半径)だから△AOCは二等辺三角形になり
∠ACO=∠CAO
∠AOD=∠ACO+∠CAO
=2×∠ACO
同様にして，BO=CO(=半径)だから△BOCは二等辺三角形になり
∠BCO=∠CBO
∠BOD=∠BCO+∠CBO
=2×∠BCO
両辺をそれぞれ足すと
∠BOA=2×∠BCA
ただし，∠BOAは図のように，優角（180°よりも大きい角）の方とする
|