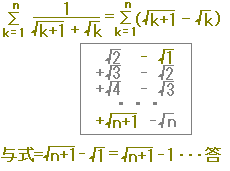|
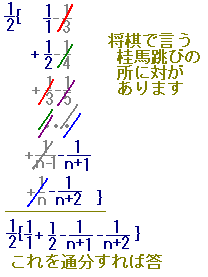
■小中学校で異分母の分数の足し算・引き算をするときには,通分によって行います.例: ■次に説明する「部分分数分解」は,一言で言えば「通分の逆」です.
■以上の内容についての理論的な説明: 分数に限らず,一般に 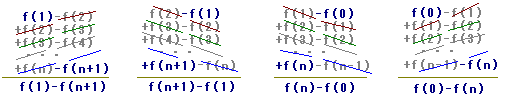
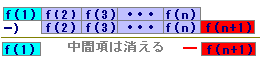
■一般に,(ある式)=f(k+1)−f(k)となる式f(k)は,元の式の次数を1次上げたものに見つかります(数IIで習う積分と同じです.):例1,例2の式はk−2なので、k-1の式の差で表現できます.例3の式はk−1/2なので、k+1/2の式の差で表現できます.例4の式はk3なので、k4の式の差で表現できます.(元の式がk-1のときはどうにもなりません:1+1/2+1/3+1/4+・・・.) ■上記の縦書きの変形で,高校の定期試験,大学の入学試験などにも十分対応できると考えられますが,さらに美的・論理的な変形を好まれる場合には次のように記述するとよいでしょう.
左辺に等しいものを右辺から見つけなさい.(この右辺は,答案の最終形ではさらに通分などによりまとめるものとしますが,ここでは途中経過で表示します.)左辺から1つ選び,続けて右辺から1つ選びなさい.合っていれば消えます.
|
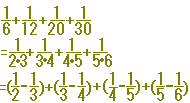
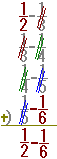 ・・・答は1/3
・・・答は1/3