曲線の長さ

(2.4)　
放物線
$y=x^2 (0\leq x \leq 1)$
の長さを $L_1$ とし，放物線
$y=\frac{1}{2}x^2 (0\leq x \leq 2)$
の長さを $L_2$ とするとき， $L_1$ ， $L_2$ の関係は？

（答案）
$y_1=x^2 (0\leq x \leq 1)$
とおくと
$y_1'=2x$
$L_1=\int_0^1 \sqrt{1+ (y_1')^2} dx=\int_0^1 \sqrt{1+ 4x^2} dx$ …(1)

$y_2=\frac{1}{2}x^2 (0\leq x \leq 2)$
とおくと
$y_2'=x$
$L_2=\int_0^2 \sqrt{1+ (y_2')^2} dx=\int_0^2 \sqrt{1+ x^2} dx$ …(2)

x=2tとおく置換積分を行うと

x	0 → 2
t	0 → 1

$\frac{dx}{dt}=2$

(2)を変形すると
$L_2=\int_0^1 \sqrt{1+ t^2} \cdot 2dt$
$=2\int_0^1 \sqrt{1+ t^2} dt$
$=2L_1$ …（答）

（参考１）
$\int \sqrt{x^2 + A} dx(A \neq 0)$ の積分計算を行うと
$\frac{1}{2}(x\sqrt{x^2+ A}+ A log|x+\sqrt{x^2 + A}|)$
になりますが，この「公式」を覚えるのは大変ですし，高校生が覚える必要もないでしょう．また，三角関数を経由して置換積分で求めるのも長い道のりになります．
　ここでは，定積分を数値に直さずに比較だけを行う問題にしました．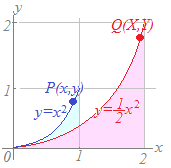

（参考２）
$y=\frac{1}{2}x^2 (0\leq x \leq 2)$
上の点を $Q(X,Y)$ とすると
$X=2x, Y=2y$ となる点 $P(x,y)$ は
$(2y)=\frac{1}{2}(2x)^2 (0\leq x \leq 1)$
すなわち
$y=x^2 (0\leq x \leq 1)$
上にあります．
　したがって，これら２つの曲線は原点を中心として相似比１：２の相似図形になります．相似図形については，面積比（例えば右図の水色の図形［下は重なって見えていない］と桃色の図形）は１：４ですが，辺の長さの比は１：２になります．この辺の長さの比は，この問題のように曲線になっていても相似比と一致します．

←例と答に戻る