|
■回転と拡大
【単位円上の複素数の積→偏角は和になる】
(解説)(cosα+i sinα)(cosβ+i sinβ)=cos(α+β)+i sin(α+β)…(1) 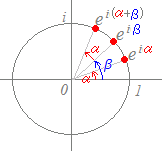 (cosα+i sinα)(cosβ+i sinβ) =cosαcosβ+icosαsinβ+isinαcosβ+i2sinαsinβ =(cosαcosβ−sinαsinβ)+i(cosαsinβ+sinαcosβ) ここで三角関数の加法定理を用いると cos(α+β)+i sin(α+β) になる.
【単位円上の複素数の商→偏角は差になる】
(解説)
=cos(α−β)+i sin(α−β)…(2)
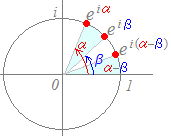
=
=
分母はcos2β+sin2β=1になるから=cosαcosβ+sinαsinβ+i(sinαcosβ−cosαsinβ) ここで三角関数の加法定理を用いると cos(α−β)+isin(α−β) になる. |
【問題1】 次の複素数を求めてください.
偏角の和を求めます.
+= cos+i sin=i…(答)
公式が適用できるように,a+biの形にします.
そのとき,sin(−θ)=−sinθ, cos(−θ)=cosθとなることに注意します. (cos+i sin )(cos(−)+i sin(− )) そこで,偏角の和を求めます. +(− )= cos+i sin=+i…(答)
(cos+i sin )2=(cos+i sin )(cos+i sin )
=cos+i sin=i この頁ではまだ取り上げていないが,次のド・モアブルの定理を使ってもよい. (cosθ+i sinθ)n=cos nθ+i sin nθ(nは整数) これにより 2×= cos+i sin=i…(答)
偏角の差を求めます.
−=−
cos(− )+i sin(− )=−i…(答) |
|
■複素数の極形式
複素数の2通りの表し方
(1) (実部)+i(虚部) の形 (2) 絶対値×(cosθ+i sinθ) の形(←これが極形式)
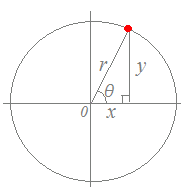
○右図4のように,半径rの円を描くと
sinθ=
cosθ=
だから
x=rcosθ
になります.y=rsinθ したがって,
x+yi=rcosθ+irsinθ=r(cosθ+isinθ)
という形で書くことができます.○x+yiをr(cosθ+isinθ)に直すときは,
r=
によって,絶対値rを求めることができます.○複素数の絶対値(大きさ)は,その複素数の原点からの距離を表しています. ■複素数の積商の図形的な意味
【複素数の掛け算は回転・拡大】
複素数z1=r1(cosθ1+sinθ1)にz2=r2(cosθ2+sinθ2)を掛けると
z1z2=r1r2(cos(θ1+θ2)+sin(θ1+θ2))
となるので,これらの積は元の複素数z1の大きさr1をr2倍し,偏角θ1にθ2を加えたものになります.このように,偏角θ2,大きさr2の複素数を掛けると,これらで表される角度と大きさだけ「回転と拡大」を行うことになります. 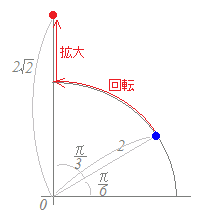 【例1】
【例1】
2(cos+i sin)
は,絶対値が2で偏角がの複素数(青丸)これに
(cos+i sin)
を掛けると,回転して, 倍したものになる(赤丸)
2(cos+i sin)×(cos+i sin)
=2(cos+i sin)=2i
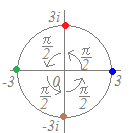 【例2】
【例2】3=3(cos0+i sin0)は,絶対値が3で偏角が0の複素数(青丸) これに
i=cos+i sinを掛けると,
回転したものになる(赤丸:3i) さらに,iを掛けると,回転したものになる(緑丸:−3) さらに,iを掛けると,回転したものになる(茶丸:−3i) さらに,iを掛けると,回転したものになる(青丸:3)
【複素数の割り算は逆回転・縮小】
複素数z1=r1(cosθ1+sinθ1)をz2=r2(cosθ2+sinθ2)で割ると
==(cos(α−β)+isin(α−β))
←(4)
となるので,この商は元の複素数z1の大きさr1をr2で割り,偏角θ1からθ2を引いたものになります.このように,偏角θ2,大きさr2の複素数で割ると,これらで表される角度と大きさだけ「逆回転と縮小」を行うことになります. 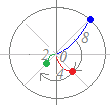 【例1】
【例1】8(cos+i sin)=4+4iは, 絶対値が8で偏角がの複素数(青丸) これを
2(cos+i sin)=2iで割ると,
時計回りに回転して,絶対値を半分にしたものになる.(赤丸:) == ==−2i+2=2−2i さらに,2iで割ると,時計回りに回転して,絶対値を半分にしたものになる. (緑丸:−−i) 【問題2】
(1)次の図において,青で示した点は複素数
z1=2(cos+i sin )
を表しています.もう一つの複素数を
z2=(cos+i sin )
とするとき,これらの積z1z2を次の複素数平面上で示してください.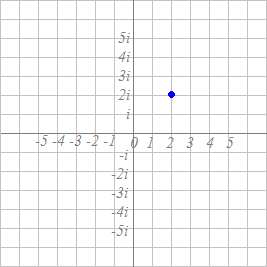 解説
z1,z2の絶対値は各々2,だから
z1z2の絶対値は2×=4
z1,z1の偏角は各々だから
z1z2の偏角は+=
になります.したがって,
z1z2=4(cos+i sin )=4i
をポイントします.
右上に続く→↑
|
図4
 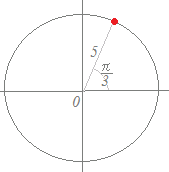 右図の赤で示した点が表す複素数は
右図の赤で示した点が表す複素数は
5(cos+i sin)
=5(+i)
=+i
→続き
(2)次の図において,青で示した点は複素数
z1=2(cos+i sin )
を表しています.もう一つの複素数を
z2=cos−i sin
とするとき,これらの積z1z2を次の複素数平面上で示してください.
解説
sin(−θ)=−sinθ, cos(−θ)=cosθだから
z2=cos(− )+i sin(− )と書ける.
z1,z2の絶対値は各々2,1だから
z1z2の絶対値は2×1=2
z1,z1の偏角は各々, −だから
z1z2の偏角は−=−
になります.したがって,
z1z2=2(cos(− )+i sin(− )=2−2i
をポイントします.
(3)次の図において,赤で示した点は複素数
z1=3(cos+i sin )
を表しています.もう一つの複素数を
z2=3(cos+i sin )
とするとき,これらの商を次の複素数平面上で示してください.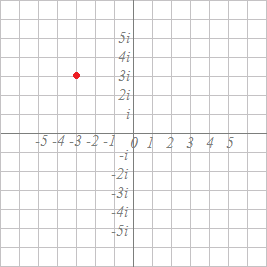
解説
z1,z2の絶対値は各々3,3だから
の絶対値は=
z1,z1の偏角は各々, だから
の偏角は−=
になります.したがって,
=(cos+i sin )=1+i
をポイントします.
(4)次の図において,赤で示した点は複素数
z1=3(cos+i sin )
を表しています.もう一つの複素数を
z2=(cos−i sin )
とするとき,これらの商を次の複素数平面上で示してください.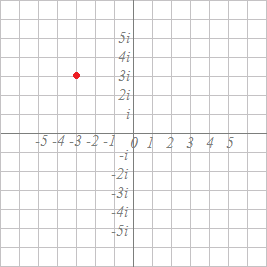
解説
sin(−θ)=−sinθ, cos(−θ)=cosθだから
z2=(cos(− )+i sin(− )と書ける.
z1,z2の絶対値は各々3,だから
の絶対値は=3
z1,z1の偏角は各々, −だから
の偏角は−(− )=
になります.したがって,
=3(cos+i sin )=−3i
をポイントします.
|