次の◎は必ず覚えて覚えておくべきものです.○はどうしてもとは言えませんが,これを知っていると多くの問題で答案の見通しがよくなります.
【要点】
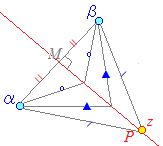
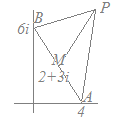
◎(1) 中学校の数学で習ったように,2定点 A(α), B(β)からの距離が等しい点 P(z)をつないでいくと, ABの垂直二等分線になります.
だから,
|z−α|=|z−β|
を満たす点 zの軌跡は,線分 ABの垂直二等分線になります.
※この方程式はPAとPBの長さが等しいPA=PBということだけを指定しているので
1) PAやPBの長さは変化する(一定ではない)ことに注意
2) PAとPBは必ずしも一直線上にはなく,ABの中点M以外の点では,AP, PBは折れ線になることに注意
○(2) 高校数学の円の方程式やベクトルのところで習うように,2定点 A(α), B(β)からの距離の比が一定である点の軌跡は, アポロニウスの円になります.
「アポロニウスの円」というのは,変な形の円につけられた名前ではなく,ちゃんとした普通の円であるがアポロニウスという数学者が研究したもので「描き方」につけられた名前
地中海風スパゲッティという感じで,アポちゃん風の円の描き方と言っているようなもの
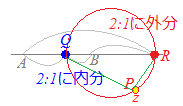
この公式をうまく使うには,次のように3点 A, B, Pが一直線上に並ぶ特別な場合,すなわち内分点と外分点を考えるとよい.
m|z−α|=n|z−β|( m≠n, n>0, n>0)
を満たす点 zの軌跡は,
2点A, Bをn:mに内分する点と
2点A, Bをn:mに外分する点を
直径の両端とする円になる.
※ m=n (gt;0)のときは円にならず,(1)で述べた垂直二等分線になります.
(2)の証明
A, Bをm:nに内分する点をQ,m:nに外分する点をRとする.
垂直関係の証明はベクトルの方が簡単なので
 \( \displaystyle \overrightarrow{PA}=\vec{a},\hspace{3px}\overrightarrow{PB}=\vec{b} \)とおいて, \( \displaystyle \overrightarrow{PA}=\vec{a},\hspace{3px}\overrightarrow{PB}=\vec{b} \)とおいて, \( \displaystyle \overrightarrow{PQ}\cdot\overrightarrow{PR}=0 \)となることを示せばよい. \( \displaystyle \overrightarrow{PQ}\cdot\overrightarrow{PR}=0 \)となることを示せばよい.
 \( \displaystyle \overrightarrow{PQ}=\frac{n\vec{a}+ m\vec{b}}{m+ n},\hspace{3px}\overrightarrow{PR}=\frac{-n\vec{a}+ m\vec{b}}{m-n} \) \( \displaystyle \overrightarrow{PQ}=\frac{n\vec{a}+ m\vec{b}}{m+ n},\hspace{3px}\overrightarrow{PR}=\frac{-n\vec{a}+ m\vec{b}}{m-n} \)
だから
 \( \displaystyle \overrightarrow{PQ}\cdot\overrightarrow{PR}=\frac{n\vec{a}+ m\vec{b}}{m+ n}\cdot\frac{-n\vec{a}+ m\vec{b}}{m-n} \) \( \displaystyle \overrightarrow{PQ}\cdot\overrightarrow{PR}=\frac{n\vec{a}+ m\vec{b}}{m+ n}\cdot\frac{-n\vec{a}+ m\vec{b}}{m-n} \)
 \( \displaystyle =\frac{-n^2\mid\vec{a}\mid^2-mn\vec{a}\vec{b}+ mn\vec{a}\vec{b}+ m^2\mid\vec{b}\mid^2}{m^2-n^2} \) \( \displaystyle =\frac{-n^2\mid\vec{a}\mid^2-mn\vec{a}\vec{b}+ mn\vec{a}\vec{b}+ m^2\mid\vec{b}\mid^2}{m^2-n^2} \)
 \( \displaystyle =\frac{ m^2\mid\vec{b}\mid^2-n^2\mid\vec{a}\mid^2}{m^2-n^2} \) \( \displaystyle =\frac{ m^2\mid\vec{b}\mid^2-n^2\mid\vec{a}\mid^2}{m^2-n^2} \)
ここで, \( \displaystyle \mid\vec{a}\mid\hspace{3px}:\hspace{3px}\mid\vec{b}\mid =m:n \)のとき,分子が0になるから \( \displaystyle \mid\vec{a}\mid\hspace{3px}:\hspace{3px}\mid\vec{b}\mid =m:n \)のとき,分子が0になるから
 \( \displaystyle \overrightarrow{PQ}\cdot\overrightarrow{PR}=0 \) \( \displaystyle \overrightarrow{PQ}\cdot\overrightarrow{PR}=0 \)
したがって,PはQRを直径の両端とする円周上にある.
※ Pが Qや Rに一致するとき,  \( \displaystyle \overrightarrow{PA} \) \( \displaystyle \overrightarrow{PA} \)と  \( \displaystyle \overrightarrow{PB} \) \( \displaystyle \overrightarrow{PB} \)が垂直だとは(高校では)言わないが,上の内積は0になるので, Qや R自体も軌跡に含まれる.
【例題2.1】
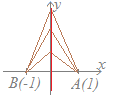
複素数平面において,方程式 |z+1|=|z−1|を満たす点 zの全体はどのような図形か答えよ.
(愛知教育大2016年)
 (解答)
(解答)
2定点A(1), B(−1)からの距離が等しい点の軌跡だから,2点ABの垂直二等分線すなわち虚軸になる.
【例題2.2】
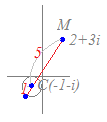
複素数平面において,等式 2|z−4|=3|z−3i|を満たす点 zの全体はどのような図形を表すか.ただし iは虚数単位とする.
(札幌医科大2016年)
(解答)
2定点からの距離の比が一定(≠1)となる動点の軌跡は,アポロニウスの円になる.
2定点A(4), B(3i)を結ぶ線分2定点ABを3:2に内分する点をQ,3:2に外分する点をRとする.
 \( \displaystyle Q:\hspace{10px}\frac{2\times 4+3\times 3i}{3+ 2}=\frac{8+ 9i}{5} \) \( \displaystyle Q:\hspace{10px}\frac{2\times 4+3\times 3i}{3+ 2}=\frac{8+ 9i}{5} \)
 \( \displaystyle R:\hspace{10px}\frac{-2\times 4+ 3\times 3i}{3-2}=-8+ 9i \) \( \displaystyle R:\hspace{10px}\frac{-2\times 4+ 3\times 3i}{3-2}=-8+ 9i \)
求める軌跡はQRを直径の両端とする円になる.
中心は,QRの中点
}{2}=\frac{-32%2B 54i}{10}=\frac{-16%2B 27i}{5}) \( \displaystyle \frac{\frac{8+ 9i}{5}+(-8+ 9i)}{2}=\frac{-32+ 54i}{10}=\frac{-16+ 27i}{5} \) \( \displaystyle \frac{\frac{8+ 9i}{5}+(-8+ 9i)}{2}=\frac{-32+ 54i}{10}=\frac{-16+ 27i}{5} \)
半径は \( \displaystyle \frac{QR}{2} \) \( \displaystyle \frac{QR}{2} \)
}{2}\mid=\mid \frac{48-36i}{10}\mid) \( \displaystyle \mid\frac{QR}{2}\mid=\mid\frac{\frac{8+ 9i}{5}-(-8+ 9i)}{2}\mid=\mid \frac{48-36i}{10}\mid \) \( \displaystyle \mid\frac{QR}{2}\mid=\mid\frac{\frac{8+ 9i}{5}-(-8+ 9i)}{2}\mid=\mid \frac{48-36i}{10}\mid \)
 \( \displaystyle =\mid\frac{24-18i}{5}\mid \) \( \displaystyle =\mid\frac{24-18i}{5}\mid \)
}{5}\mid=\frac{6}{5}\mid4-3i\mid=\frac{6}{5}\times 5=6) \( \displaystyle =\mid\frac{6(4-3i)}{5}\mid=\frac{6}{5}\mid4-3i\mid=\frac{6}{5}\times 5=6 \) \( \displaystyle =\mid\frac{6(4-3i)}{5}\mid=\frac{6}{5}\mid4-3i\mid=\frac{6}{5}\times 5=6 \)
したがって
 \( \displaystyle \frac{-16+ 27i}{5} \)を中心とする半径 \( \displaystyle \frac{-16+ 27i}{5} \)を中心とする半径 \( \displaystyle 6 \)の円になる. \( \displaystyle 6 \)の円になる.
※答案の中に「アポロニウスの円」という用語を入れることにより,それが教科書や参考書に書いてある公式であることをほのめかし,根拠なしとして減点されるのを防ぐ
→右上に続く
|
【問題2】 選択肢の中から正しい答を選んでください.(クリックする)
(1)
aを実数の定数とする.複素数 zが  \( \displaystyle z\bar{z}-ia\bar{z}+ iaz=1 \) \( \displaystyle z\bar{z}-ia\bar{z}+ iaz=1 \)をみたしながら動くとき,複素数平面上で zの表す点はどのような図形をえがくか.ただし,  \( \displaystyle \bar{z} \) \( \displaystyle \bar{z} \)は zに共役な複素数を表す.
(宮城教育大2005年.
[当教材では選択問題に変更])
円になる
(中心)
(半径)
 \( \displaystyle \mid z-ia\mid=\sqrt{a^2+ 1} \) \( \displaystyle \mid z-ia\mid=\sqrt{a^2+ 1} \)
だから
半径は  \( \displaystyle \sqrt{a^2+1} \) \( \displaystyle \sqrt{a^2+1} \)
(2)
複素数 zが  \( \displaystyle \mid z-1\mid=2\mid z+1\mid \) \( \displaystyle \mid z-1\mid=2\mid z+1\mid \)をみたしながら動くとき
(i) 複素数平面上で zの表す点はどのような図形をえがくか.
(ii) 複素数平面上で  \( \displaystyle w=\frac{3z+ 1}{z+ 3} \) \( \displaystyle w=\frac{3z+ 1}{z+ 3} \)の表す点はどのような図形をえがくか.ただし, z≠−3とする.
(宮城教育大2005年.[当教材では選択問題に変更])
(i) 2定点からの距離の比が一定(≠1)である動点の軌跡はアポロニウスの円になる.
(中心)
2点 1, −1を結ぶ線分を2:1に内分する点Qは
}{2%2b 1}=-\frac{1}{3}&chco=aa4422) \( \displaystyle \frac{1\times 1+ 2\times (-1)}{2+ 1}=-\frac{1}{3} \) \( \displaystyle \frac{1\times 1+ 2\times (-1)}{2+ 1}=-\frac{1}{3} \)
2点 1, −1を結ぶ線分を2:1に外分する点Rは
}{2-1}=-3&chco=aa4422) \( \displaystyle \frac{-1\times 1+ 2\times (-1)}{2-1}=-3 \) \( \displaystyle \frac{-1\times 1+ 2\times (-1)}{2-1}=-3 \)
これらQ,Rの中点が円の中心だから
}{2}=-\frac{5}{3}&chco=aa4422) \( \displaystyle \frac{-\frac{1}{3}+(-3)}{2}=-\frac{5}{3} \) \( \displaystyle \frac{-\frac{1}{3}+(-3)}{2}=-\frac{5}{3} \)
wz+3w=3z+1
(w−3)z=1−3w
 \( \displaystyle z=\frac{1-3w}{w-3} \) \( \displaystyle z=\frac{1-3w}{w-3} \)
これを |z−1|=2|z+1|に代入すると
 \( \displaystyle \mid\frac{1-3w}{w-3}-1\mid=2\mid\frac{1-3w}{w-3}+ 1\mid \)
|1−3w−w+3| \( \displaystyle \mid\frac{1-3w}{w-3}-1\mid=2\mid\frac{1-3w}{w-3}+ 1\mid \)
|1−3w−w+3|
=2|1−3w+w−3|
|−4w+4|=2|−2w−2|
4|w−1|=4|w+1|
|w−1|=|w+1|
2点 1, −1からの距離が等しい点の軌跡になるから,虚軸
i)の結果: zの軌跡が,中心  \( \displaystyle -\frac{5}{3} \) \( \displaystyle -\frac{5}{3} \)半径  \( \displaystyle \frac{4}{3} \) \( \displaystyle \frac{4}{3} \)の円になることから出発してもよい.
 \( \displaystyle \mid\frac{1-3w}{w-3}+ \frac{5}{3}\mid=\frac{4}{3} \)
|3(1−3w)+5(w−3)| \( \displaystyle \mid\frac{1-3w}{w-3}+ \frac{5}{3}\mid=\frac{4}{3} \)
|3(1−3w)+5(w−3)|
=4|w−3|
|−4w−12|=4|w−3|
4|w+3|=4|w−3|
|w+3|=|w−3|
2点 −3, 3からの距離が等しい点の軌跡になるから,虚軸
(3)
iを虚数単位とする.複素数 zが等式 |iz+3|=|2z−6|を満たすとき,次の問いに答えよ.
(1) この等式を満たす点 z全体は,どのような図形を表すか答えよ.
(秋田大2016年.[当教材では選択問題に変更])
左辺の絶対値記号の中に −iを掛けても等式は成り立つ( |−i|=1だから)
|−i2z−3i|=|2z−6|
|z−3i|=2|z−3|
2定点 3i, 3からの距離の比が2:1である点の軌跡はアポロニウスの円になる.
3i, 3を2:1に内分する点は
 \( \displaystyle \frac{1\times 3i+ 2\times 3}{2+ 1}=2+ i \)
3i, 3 \( \displaystyle \frac{1\times 3i+ 2\times 3}{2+ 1}=2+ i \)
3i, 3を2:1に外分する点は
 \( \displaystyle \frac{-1\times 3i+ 2\times 3}{2-1}=6-3i \) \( \displaystyle \frac{-1\times 3i+ 2\times 3}{2-1}=6-3i \)
これらの中点が円の中心になる
%2B(6-3i)}{2}=4-i&chco=aa4422) \( \displaystyle \frac{(2+ i)+(6-3i)}{2}=4-i \) \( \displaystyle \frac{(2+ i)+(6-3i)}{2}=4-i \)
半径は
-(2%2B i)}{2}\mid=\mid 2-2i\mid=2\sqrt{2}&chco=aa4422) \( \displaystyle \mid\frac{(6-3i)-(2+ i)}{2}\mid=\mid 2-2i\mid=2\sqrt{2} \) \( \displaystyle \mid\frac{(6-3i)-(2+ i)}{2}\mid=\mid 2-2i\mid=2\sqrt{2} \)
(別解:  \( \displaystyle \mid z\mid^2=z\bar{z} \) \( \displaystyle \mid z\mid^2=z\bar{z} \)の変形を使った答案)
 \( \displaystyle \mid iz+ 3\mid^2=\mid 2z-6\mid^2 \) \( \displaystyle \mid iz+ 3\mid^2=\mid 2z-6\mid^2 \)
(-i\bar{z}%2B 3)=(2z-6)(2\bar{z}-6)&chco=aa4422) \( \displaystyle (iz+ 3)(-i\bar{z}+ 3)=(2z-6)(2\bar{z}-6) \) \( \displaystyle (iz+ 3)(-i\bar{z}+ 3)=(2z-6)(2\bar{z}-6) \)
 \( \displaystyle -i^2z\bar{z}+ 3iz-3i\bar{z}+ 9=4z\bar{z}-12z-12\bar{z}+ 36 \) \( \displaystyle -i^2z\bar{z}+ 3iz-3i\bar{z}+ 9=4z\bar{z}-12z-12\bar{z}+ 36 \)
z%2B(-12%2B 3i)\bar{z}%2B 27=0&chco=aa4422) \( \displaystyle 3z\bar{z}-(12+ 3i)z+(-12+ 3i)\bar{z}+ 27=0 \) \( \displaystyle 3z\bar{z}-(12+ 3i)z+(-12+ 3i)\bar{z}+ 27=0 \)
z%2B(-4%2B i)\bar{z}%2B 9=0&chco=aa4422) \( \displaystyle z\bar{z}-(4+i)z+(-4+ i)\bar{z}+ 9=0 \) \( \displaystyle z\bar{z}-(4+i)z+(-4+ i)\bar{z}+ 9=0 \)
\}\{\bar{z}-(4%2B i)\}-(4-i)(4%2B i)%2B 9=0&chco=aa4422) \( \displaystyle \{z-(4-i)\}\{\bar{z}-(4+ i)\}-(4-i)(4+i)+ 9=0 \) \( \displaystyle \{z-(4-i)\}\{\bar{z}-(4+ i)\}-(4-i)(4+i)+ 9=0 \)
 \mid^2=8&chco=aa4422) \( \displaystyle \mid z-(4-i) \mid^2=8 \) \( \displaystyle \mid z-(4-i) \mid^2=8 \)
 \mid=2\sqrt{2}&chco=aa4422) \( \displaystyle \mid z-(4-i) \mid=2\sqrt{2} \) \( \displaystyle \mid z-(4-i) \mid=2\sqrt{2} \)
したがって,
中心が 4−iで半径が  \( \displaystyle 2\sqrt{2} \) \( \displaystyle 2\sqrt{2} \)の円になる
|
 (2) 動点P(z)が方程式
(2) 動点P(z)が方程式 (3) 動点P(z),定点A(α)について
(3) 動点P(z),定点A(α)について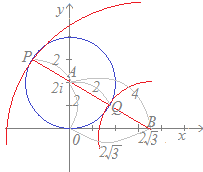 (解答)
(解答)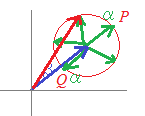 (三角不等式を用いた別解)
(三角不等式を用いた別解)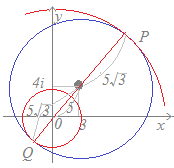 中心が3+4i,半径が
中心が3+4i,半径が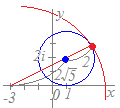 |z−1−2i|=2
|z−1−2i|=2 ◎(1) 中学校の数学で習ったように,2定点
◎(1) 中学校の数学で習ったように,2定点 この公式をうまく使うには,次のように3点
この公式をうまく使うには,次のように3点 (解答)
(解答)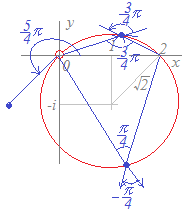 (別解)
(別解)
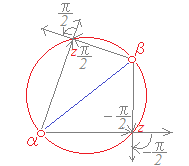 中学校で習う円周角の定理の逆(円周角が直角ならば弦は直径になる)を考える.
中学校で習う円周角の定理の逆(円周角が直角ならば弦は直径になる)を考える.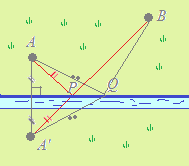 (1)
(1)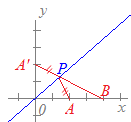 (解答)
(解答)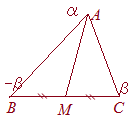 【中線定理】(またはパップスの定理)
【中線定理】(またはパップスの定理)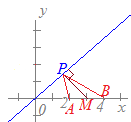
 円の中心
円の中心