 【解説】二項定理 【解説】二項定理通常,式の展開は次のような順序で,「総当たりで」掛けると考えることが多いが,二項定理,多項定理の解説はこの方法では分かりにくいので,「代表選手の選び方」で解説してみる. 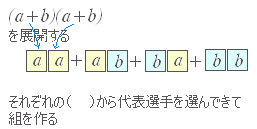 右図のように各々の( )からどちらか1つの項 a , b を選んで取り出し,合計 2 個からなる文字の組を考える. 右図のように各々の( )からどちらか1つの項 a , b を選んで取り出し,合計 2 個からなる文字の組を考える.○「同じものがあるときの順列」で考える方法 (a+b)n を展開したときの an−rbr の係数を考える. 各々の( )からどちらか1つの項 a , b を選んで取り出し,合計 n 個からなる文字の組を考える.  そこで,abb···ab など n 個の文字のうち,a が n−r 個,b が r 個ある順列を並べ替えてできる順列の総数を数える. 全部異なるものが n 個あるときは,並べ替えてできる順列は n! 個あるが,a は同じものなので,その内部交換でできる (n−r)! 通りは別のものができないから, n! 個とすると (n−r)! 倍だけ数え過ぎで,正しくは 通り. 同様にして,b も同じものなので,その内部交換でできる r! 通りは別のものができないから,上のように 通りとすると r! 倍だけ数え過ぎで,正しくは 通り. 結局,a が n−r 個,b が r 個,それぞれ同じものがある合計 n 個の文字 abb···ab を並べ替えてできる順列の総数は, 通りだから,上のように代表の組を作るとan−rbr は 回登場する. これらの同類項をまとめると,係数は になる. (■→続く■) |
(■→続き■) 例えば (a+b)5 を展開するとき,左図のような選び方をすると,abbab という項が1つできる.これは,a2b3 になる. しかし,a2b3 になるのはこれだけではない.a2b3 になるものを全部並べると,次のようになる. abbab , abbba baabb , babab babba , bbaab bbaba , bbbaa ○ 組合せで考える方法 a が n−r 個,b が r 個,それぞれ同じものがある合計 n 個の文字 abb···ab を並べ替えてできる順列の総数を,図のように1~nのn個の番号札をあらかじめ用意しておき,b の行き先の番号札をもらう方法で考える. (a の行き先の番号札を n−r 個もらうと考えてもよい.) 上の図のように,2,3,・・・,nの札をもらったとき,その場所に b が入ると決めておく( a の場所は,自動的に決まり,残りの n−r 個の場所となる.)と,b の行き先 r 個の番号札のもらい方が並べ方の総数に等しく,nCr すなわち 通りになる. an−rbr は 回登場するから, これらを同類項をまとめると,係数は になる. |
|
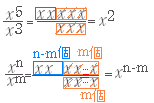
【解説】多項定理 二項定理のときと同様に「同じものがあるときの順列」で考えると (a+b+c)n を展開したとき,apbqcr が登場する回数は, a が p 個,b が q 個,c が r 個それぞれ同じものがある合計 n 個の文字 abbc···ab を並べ替えてできる順列の総数になり, 通り apbqcr を同類項としてまとめると,その係数は |
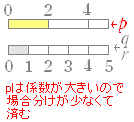
○ 組合せで考える方法 多項定理は,最近の高校の教科書では,組合せを2段階適用して解説されている. 1~nまで合計n個の番号札をあらかじめ用意しておき,文字 a の行き先 p 個,文字 b の行き先 q 個,文字 c の行き先 r 個をもらう方法を数えると, a の札のもらい方は nCp 通り, その各々について,残り n−p 枚の番号札のうち b の札のもらい方は n−pCq 通り, (残りは自動的に c の札となる.) もらい方の総数は,nCp×n−pCq= = ここで,n−p−q=r であるから, に等しい. |
 [*]
[*]