|
■重積分:変数変換.ヤコビアン
○ 【１変数の場合を振り返ってみる】
置換積分の公式f(x)dx=f(g(t)) g’(t)dt
この公式が成り立つためには，その区間において「１対１の対応であること」「積分可能であること」など幾つかの条件を満たしていなけばならないが，これは満たされているものとする．
においては，
のように，積分区間，被積分関数，積分変数の各々を対応するものに書き換えることによって，変数変換を行うことができます． その場合において，積分変数dxは，単純にdtに変わるのではなく，右図１に示されるようにg’(t)dtに等しくなります．
=g’(t)は極限移項前の分数の形では≒g’(t)
つまりΔx≒g’(t)Δt 極限移項したときの記号としてdx=g’(t)dt
○ 【２変数の重積分の場合】
重積分f(x,y)dxdyにおいて，積分変数x, yを 
x=x(u, v)y=y(u, v)
右図２のように
(dx, 0)は(du , dv )に移され
(0, dy)は(du , dv )に移される．
このとき，図３のように面積要素は
dxdy=|dudv−dudv|
=|−|dudv
のように変換されます．
【要点】
−は負の値をとることもあり，
面積要素として計算するには，これを正の符号に変えます．
ここで，
|−|
は，ヤコビ行列J=
の行列式すなわちヤコビアン（関数行列式）det(J)= の絶対値|det(J)|を表します．
x=x(u,v), y=y(u,v)により，xy平面上の領域Dがuv平面上の領域Eに移されるとき
面積要素は|det(J)|倍になる．ヤコビアンの絶対値を|det(J)|で表すと |det(J)|=|−| f(x,y)dxdy=f(x(u,v),y(u,v))|det(J)|dudv
この公式が成り立つためには，その領域において「１対１の対応であること」「積分可能であること」など幾つかの条件を満たしていなけばならないが，これは満たされているものとする．
|
図１
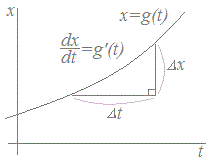 （縦の長さ）＝（横の長さ）×（傾き） になる． 図２ 
【２つのベクトルで作られる平行四辺形の面積】
（解説）次の図のような２つのベクトル=(a, b), =(c, d)で作られる平行四辺形の面積Sは S=|ad−bc| で求められます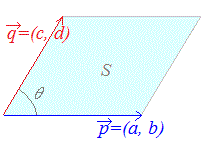．  Sは  の絶対値となります．S=||||sinθ …(1) において，ベクトルの内積と角度の関係式 · =ac+bd=||||cosθ …(2) から，cosθを求めて sinθ= (>0) …(3) に代入すると（途中経過省略） S= = =|ad−bc| となることを示すことができます．
【用語と記号のまとめ】
ヤコビ行列 J=  ヤコビアン det(J)= ヤコビアンの絶対値 |det(J)|=|−| |
|||||||
|
【例１】
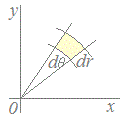直交座標xyから極座標rθに変換するとき，
x=rcosθ, y=rsinθ
だから =cosθ, =−rsinθ =sinθ, =rcosθ det(J)=cosθ·rcosθ−(−rsinθ)·sinθ =rcos2θ+rsin2θ=r (>0) したがって f(x,y)dxdy=f(x(r,θ),y(r,θ))·r·drdθ |
【例２】
重積分(x+y)2dxdy (D : 0≦x+y≦1, |x−y|≦1) を変数変換u=x+y, v=x−yを用いて行うとき，
E : 0≦u≦1, −1≦v≦1
x=, y= （旧変数←新変数の形） =, =, =− det(J)=(−)−=− (<0) だから |det(J)|= (x+y)2dxdy=u2dudv du dv=dv=dv
==
|
|||||||
|
問１次の重積分を計算してください．
1
2
3
4
5
HELPdxdy (D : x2+y2≦1)
極座標x=rcosθ, y=rsinθに変換すると，
D : x2+y2≦1 → E : 0≦r≦1, 0≦θ≦2π
dxdy=r·r drdθ=cosθ, =−rsinθ =sinθ, =rcosθ det(J)=cosθ·rcosθ−(−rsinθ)·sinθ =rcos2θ+rsin2θ=r (>0) r2dr== dθ== → 4 ※変数をx,yのままで積分を行うには，の積分を行う必要があり，さらに積分区間を− 〜 としなければならないので，多くの困難があります． |
問２次の重積分を計算してください．
1
2
3
4
4
HELPx dxdy(D :0≦x+y≦1, 0≦x−y≦1)
u=x+y, v=x−yにより変数変換を行うと，
E : 0≦u≦1, 0≦v≦1
x=, y= （旧変数←新変数の形） =, =, =− det(J)=(−)−=− (<0) だから |det(J)|= x dxdy=dudv du=+=+ (+)dv=+=+=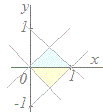 
※変数をx,yのままで積分を行うこともできるが，その場合は右図の水色，黄色の２つの領域（もしくは左右２つの領域）に分けて計算しなければならない．この問題では，上記のようにu=x+y, v=x−yと変数変換することにより，スマートに計算できるところがミソ． |
|||||||
|
問３次の重積分を計算してください．
1
2
3π
4
4
HELPcos(x2+y2)dxdy( D : x2+y2≦ )
極座標x=rcosθ, y=rsinθに変換すると，
D : x2+y2≦ → E : 0≦r≦, 0≦θ≦2π
cos(x2+y2)dxdy=cos(r2)·r drdθ=cosθ, =−rsinθ =sinθ, =rcosθ det(J)=cosθ·rcosθ−(−rsinθ)·sinθ =rcos2θ+rsin2θ=r (>0) (sin(r2))=2r cos(r2)だからr cos(r2)dr=sin(r2)+C cos(r2)·r dr=sin(r2)= dθ==π → 3 |
問４
D : |x−y|≦2, |x+2y|≦1において，次の重積分を計算してください．
{(x−y)2+(x+2y)2}dydx
1
2
3
4
5
HELP
u=x−y, v=x+2yにより変数変換を行うと，
E : −2≦u≦2, −1≦v≦1
{u2+v2}du={u2+v2}dux=, y= （旧変数←新変数の形） =, = =−, = det(J)=−(−)= (>0) だから |det(J)|= {(x−y)2+(x+2y)2}dydx ={u2+v2}dudv =+v2u=(+2v2)=+v2 2(+v2)dv=2v+v3=2(+)= |
..高卒〜大学数学のメニューに戻る
○===メニューに戻る