|
2. �O�p���̐���
�O�p���̑��݊W �����ŁC
���ȉ��ɂ����ẮC�p
�@��1�ی��̊p ����C����̊W
�@���a��
������C���̒l��
��L�̓_
�����̊W���ԈႤ���Ă͔�푽���̂Œ��ӁD
��L�̓_
���̒l�� |
|
���� (2.6) (2.7) (2.8) 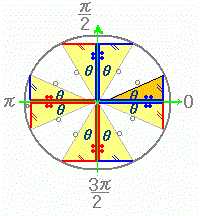
�@�E�}�̂ǂ����̋R�m�c�̖�͂̂悤�Ȑ}�`�̏������F�u�����͉E�i���j��C���i���j��Ԃŕ`���v�u�c���͏�i���j��C���i���j��Ԃŕ`���v
�@��P�ی��ix>0, y>0�j�́u���̎O�p�`���Ȃ킿�p�x ���
(2.6)←�@�܂����߂ɁC�p�x �A���ɁC���߂���̂� �c(��������)�^���a
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C (2.7)← �@���l�ɂ��ĉE�}�����̏ꏊ�ɂ��� �A���߂���̂� ��(��������)�^���a
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C (2.8)← �@���l�ɂ��ĉE�}�����̏ꏊ�ɂ��� �A���߂���̂� �c(��������)�^��(��������)
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@����́C �@�ȏ�ɂ��C
�y�v�_�z
�k�ɂ���i←�ʑ��I�Ȍ������j�p �O�p���̌`���ς��F |

���� (2.9) (2.10) (2.11) ���
(2.9)←�@�܂����߂ɁC�p�x �A���ɁC���߂���̂� �c(��������)�^���a
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C (2.10)← �@���l�ɂ��ĉE�}�����̏ꏊ�ɂ��� �A���߂���̂� ��(��������)�^���a
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C (2.11)← �@���l�ɂ��ĉE�}�����̏ꏊ�ɂ��� �A���߂���̂� �c(��������)�^��(��������)
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@����́C �@�ȏ�ɂ��C
�y�v�_�z
�@�k�ɂ���i←�ʑ��I�Ȍ������j�p �O�p���̌`���ς��F �@���߂Ă���̂� |

���� (2.12) (2.13) (2.14) ���
(2.12)←�@�܂����߂ɁC�p�x �A���ɁC���߂���̂� �c(��������)�^���a
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C (2.13) ← �@���l�ɂ��ĉE�}�����̏ꏊ�ɂ��� �A���߂���̂� ��(��������)�^���a
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C (2.14)← �@���l�ɂ��ĉE�}�����̏ꏊ�ɂ��� �A���߂���̂� �c(��������)�^��(��������)
���l���܂��D�B�Ō�ɁC��1�ی��̔Z���F�̎O�p�`�C���Ȃ킿�p�x �@�ȏ�ɂ��C
�y�v�_�z
�@�ԓ�����i←�ʑ��I�Ȍ������j�p �O�p���̌`���ς�Ȃ��F �@���߂Ă���̂� |

���� (2.15) (2.16) (2.17) ���
���l�ɂ��ĉE�}�ōl����D����͗�
���� (2.18) (2.19) (2.20) ���
���l�ɂ��ĉE�}�ōl����D����͗�
���� (2.21) (2.22) (2.23) ���
���l�ɂ��ĉE�}�ōl����D����͗�
���� (2.3) (2.4) (2.5) ���
���l�ɂ��ĉE�}�ōl����D����͗�
���� (2.24) (2.25) (2.26) ���
�P�ʉ~��� |
|
�ȒP���K
���̎����ȒP�ɂ��Ă��������D�i�萔��
(1)
�i�j
(2)
�i�j���������āC |
|
(3)

�i�ʉ��j 
(4)
�i�j
��1����

�P�ʉ~��ŁC�E�}�̂Q�̓_�̂����W�͕����������t�ɂȂ��Ă��邩��C�����̘a��0�ɂȂ� |