|
高校〜大学基礎の数学用語.公式.例
奇関数・偶関数
odd function, even function用語
例
奇関数:偶関数: グラフ
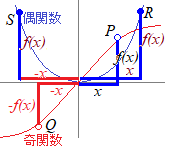
奇関数のとき
偶関数のとき
話題
♪〜言葉は独り歩きできない!
奇関数×奇関数=偶関数…(*1)
となることに注意偶関数×偶関数=偶関数…(*2) 奇関数×偶関数=奇関数…(*3) (*1)の証明 他の証明は各自でできるはず
また,
奇関数±奇関数=奇関数…(*4) 偶関数±偶関数=偶関数…(*5) も示せる.マクローリン展開において のように, 同様に, のように,
すべての関数が,偶関数か奇関数のどちらかに分類されるわけではない.偶関数±奇関数で書かれる関数,例えば,
「任意の関数は,偶関数と奇関数の和で表せる.」 (証明) は成り立つ.ここで とおくと が成り立つから, よって,任意の関数は偶関数と奇関数の和で表せる.(証明終) グラフ
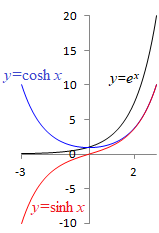
と書ける.これらの関数は, とも書かれ,双曲線関数と呼ばれる.双曲線関数 簡単復習
次の各関数が偶関数か奇関数か,根拠も付けて答えてください.(1) (2) (3) (4) (2) (3) (4) |