|
�p��
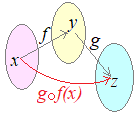
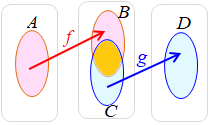
�@�W��X����Y�ւ̑Ή�
• • �قȂ� ��Ō����� �ƂȂ�Ƃ��C • �S�˂��P�ˁi�S�P�ˁj�ł���Ƃ��C�t�ʑ������݂���D • �ʑ��̓��ŁC��`��ƒl�悪�ǂ���������̏W���ł�����̂����Ƃ����D • ���̓��Œ�`��ƒl�悪�����W���ł�����̂��ϊ��Ƃ����D |
 �@�W��
�@�W���@�E�̊� (1) (2) �@���̂悤�Ɂu��ւ̎ʑ��v�łȂ��ꍇ��u1��1�̎ʑ��v�łȂ��ꍇ�ɂ́C �@����ɑ��āC�u��ւ�1��1�̎ʑ��v�u�S�P�ˁv�ɂȂ��Ă���ꍇ�ɂ́C�ǂ�
���������C�u1��1�̎ʑ��v�ɂ��Ă͌��i�ɍl���邪�C�u�^����ꂽ�����Ӗ������͈͂ŁC�Ȃ�ׂ��L���͈͂Œ�`����l����v�Ƃ���������Ƃ��āC�u��ւ̎ʑ��v�u�S�ˁv�ɂ��Ă͊ɂ₩�ɍl���Ă悢���Ƃ������D
��
�@�@���̊����Ӗ������Ȃ�ׂ��L���͈͂��l���āC �@ ��
�@�@���̊����Ӗ������Ȃ�ׂ��L���͈͂��l���āC �@ ��
�@��
�@ |
|
�d�v
�@�����
�����藧�D �� �����藧�Ƃ��C �p��
�@�i��`��ɑ�����j���ׂĂ� �i����j
�i����j�@�s���Ă���߂�C���ɖ߂邩�疾�炩 ��
��
|
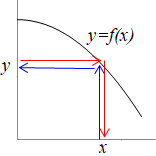
 �@���̒�`��́C�w�肪����ꍇ�͂���ɏ]���C���Ɏw�肪�Ȃ��ꍇ�́C�����Ӗ���������łȂ�ׂ��L���͈͂��Ƃ�܂��D
�@���̒�`��́C�w�肪����ꍇ�͂���ɏ]���C���Ɏw�肪�Ȃ��ꍇ�́C�����Ӗ���������łȂ�ׂ��L���͈͂��Ƃ�܂��D

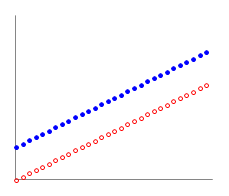 �i����j
�i����j