|
�d�v
�@�����
�i����j�@�}1�C�}2�̂悤�ɁC�قȂ� �@1��1�Ή��̊��ł́C  - �}1 - 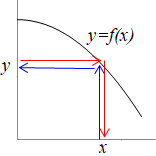 - �}2 -  - �}3 - �@�}1�C�}2�Ɛ}3���r����ƁC�}1�͒P���������C�}2�͒P���������ɂȂ��Ă��āC |
�d�v
�@���
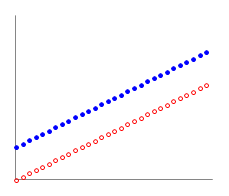 �i����j
�i����j�@�A���Ƃ����������O���C�Ⴆ�ΉE�}�̊� �Ƃ��������l����ƁC���� �@���̂悤�ɁC�t���̑��ݏ����Ƃ��āC�P�������܂��͒P�������Ƃ����������t���̂́C�A�����̏ꍇ�ł��D |
 �@�W��
�@�W���@�E�̊� (1) (2) �@���̂悤�Ɂu��ւ̎ʑ��v�łȂ��ꍇ��u1��1�̎ʑ��v�łȂ��ꍇ�ɂ́C �@����ɑ��āC�u��ւ�1��1�̎ʑ��v�u�S�P�ˁv�ɂȂ��Ă���ꍇ�ɂ́C�ǂ�
���������C�u1��1�̎ʑ��v�ɂ��Ă͌��i�ɍl���邪�C�u�^����ꂽ�����Ӗ������͈͂ŁC�Ȃ�ׂ��L���͈͂Œ�`����l����v�Ƃ���������Ƃ��āC�u��ւ̎ʑ��v�u�S�ˁv�ɂ��Ă͊ɂ₩�ɍl���Ă悢���Ƃ������D
��
�@�@���̊����Ӗ������Ȃ�ׂ��L���͈͂��l���āC �@ |
��
�@�@���̊����Ӗ������Ȃ�ׂ��L���͈͂��l���āC �@ ��
�@��
�@ |
|
�d�v
�@�����
�����藧�D �� �����藧�Ƃ��C |
�p��
�@�i��`��ɑ�����j���ׂĂ� �i����j
�i����j�@�s���Ă���߂�C���ɖ߂邩�疾�炩 ��
��
|