|
高校〜大学基礎の数学用語.公式.例
話題
無理数の指数
 となる数 となる数 に対して, に対して, の値は の値は
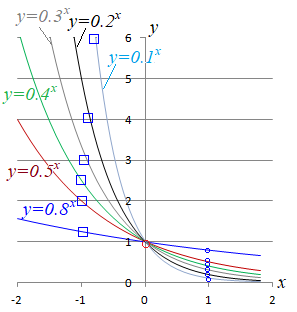
(1)  が正の整数のとき,  を  回かけた値を表す.
例

 →右図の青丸
(2)  が負の整数 ) のとき,  の逆数  を表す.
例

 →右図の茶色丸
(3)  のとき,  を表す.
例
 →右図の黒丸
(4)  (  は正の整数)のとき,  (累乗根)を表す.
例

 →右図の明緑丸
(5)  (  は正の整数)のとき,  を表す.
例

 →右図の暗緑丸
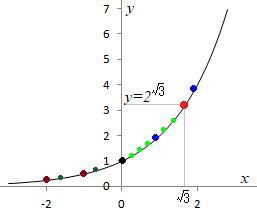
さて, のように,指数が無理数のとき, のように,指数が無理数のとき, の値はどのように定まるか? の値はどのように定まるか?
指数関数  のグラフを描くためには,  の値が  など無数にある無理数の場合の  の値を決める必要があります.これを決めなければ,グラフは穴だらけになり「連続」とか「微分」という議論ができなくなります.
 の値」は「指数が有理数のときの の値」は「指数が有理数のときの の値」の数列の極限値で定義します. の値」の数列の極限値で定義します.
例えば, の値を求めるには の値を求めるには
(6.1) まず, のように無理数を小数で表示します. のように無理数を小数で表示します.
(6.2) 次に





のように必要なだけ詳しく求めます.この数列が収束するとき,その極限値を と決めます.(次のような値になります) と決めます.(次のような値になります)
3.321997085483912805157183119647826939159120898002259...
【要約】
「指数が無理数のとき,  の値」は「指数が有理数のときの  の値」の数列の極限値で定義する.
|