← 携帯用は別頁
|
「生成AIの能力を生かす質問の仕方」(1) ・・・『できること』と『傾向』の実演レポート
※このページの内容は,2025年2月現在で,無料利用可能な日本語対応の生成AI
(Ⅰ) 数学の図形問題を生成AIに解ける形で入力するには?1. 「ChatGTP」 , 2. 「Copilot」 , 3. 「Gemini」 を用いて,数学の答案を引き出すための質問の仕方を考えたもので,「単なる個人の感想」です. 《例1》 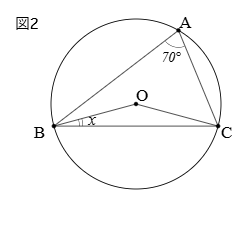
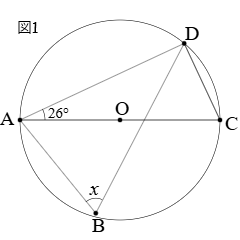 次の図が画像として示されているときに,∠xの大きさ求めたいとき
次の図が画像として示されているときに,∠xの大きさ求めたいとき1. 「ChatGTP」 ⇒ 入力欄に次のように書き込んで,Enterキーを押す
(A) 図1,図2とも問題は解けない.
\( \Large \Longrightarrow\) ① ChatGPTでは,画像はファイルの形になっているものを利用し,入力欄の左にある「+」をクリックして,画像をアップロードするとよい.(画像がWeb上にあるときは,右クリック→画像としてPCに保存してから使えばよい)(B) 図1:「D の位置関係が明確ではありません。」ということで,解答は示されない. 図2:「図の関係をもう少し詳しく説明してもらえれば、より正確な答えを導けます!」ということで,解答は示されない. (C) 図1,図2とも正しい答案が示される.64°と20° ② ChatGPTでは,問題が画像だけで示された場合,答は示されない.「質問は文章で述べるように」という旨の忠告があ. ③ (C)のように「問題文を,論理的な文章として示す」と生成AIが問題を正確に判断し,解けるようになる・・・(B)のように条件の一部が図のみで示されている場合には,判断を誤ることがある. |
2. 「Copilot」 ⇒ 入力欄に次のように書き込んで,Enterキーを押す
(A) 図1は誤答(∠x=80°),図2も誤答(∠x=70°)となる
\( \Large \Longrightarrow\) ① Copilotでは,画像はファイルの形になっているものを利用し,入力欄の左にある「+」をクリックして,画像をアップロードするとよい.(画像がWeb上にあるときは,右クリック→画像としてPCに保存してから使えばよい)(B) 正解(20°)が表示される. (C) 図1,図2とも正しい答案が示される.64°と20° ② この実験結果だけから判断すれば,2025.2月現在で,Copilotは問題が図だけで示されると,正確な情報として受けとめにくいようである. ③ (B)のように,条件の一部分が図だけにある場合でも,解けることがある. ④ (C)のように「問題文を,論理的な文章として示す」と生成AIが問題を正確に判断し,解けるようになる. |