■　極端値を削除するには

○　使用したい場面

　平均値を求めるときに，極端値，外れ値が含まれているときにはこれを取り除いて集計するのがよいと言われている．
　すなわち，平均値は，極端値・外れ値の影響を受けやすく，ものによっては最頻値（最もよく登場する値）や中央値（順序が真ん中の値）を使う方がよい場合もある．・・・例えば，庶民の中に大金持ちが1人混ざっているときに，平均収入を求めてもその平均は庶民の所得を反映していない．

　右の例1は，当サイトの ../math/su01.htm の第1問について，2009.06.19〜2009.07.31までに回答のあった462件の答案の所要時間実測値をグラフにしたものである．このグラフに示されるように所要時間は一般に左右非対称なグラフとなり，極端に大きな値がしばしば含まれている．このような実測値を単純に平均すると集団の傾向を反映せず，特定の数人の値だけを反映してしまう．

　右の例2において「元データ」はよく起こる例のイメージとして作ったもので，10人の回答者の所要時間を表わしている．このデータから平均値を計算すると1113.8となり，その平均値は「回答者10」の１人の所要時間を大きく反映している．ところが，個々のデータを見てみると4秒〜6秒に多くの値が集中しており，平均値が1113.8といっても実態からかけ離れている．

　そこで，極端値を取り除いて集団の傾向を表わす平均値をうまく取り出すにはどうすればよいかを考える．

※　Microsoft Excel には両端の値を取り除いて平均する TRIMMEAN という関数が組み込まれているが，この関数は最小値も取り除くため，ここで求めたい非対称型分布に適用してもうまくいかない．例えば TRIMMEAN(範囲,割合)において，割合を0.1としても平均は1113，割合を0.2としても平均は141となり，実態からはかけ離れた数字となる．		 例1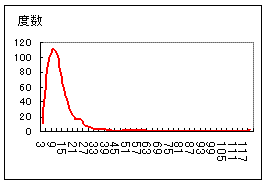

例2
　 A B C D E F
1 　 元データ 1回削除 2回削除 3回削除 4回削除
2 回答者1 4.0 4.0 4.0 4.0 4.0
3 回答者2 4.1 4.1 4.1 4.1 4.1
4 回答者3 4.3 4.3 4.3 4.3 4.3
5 回答者4 4.5 4.5 4.5 4.5 4.5
6 回答者5 5.1 5.1 5.1 5.1 5.1
7 回答者6 5.7 5.7 5.7 5.7 5.7
8 回答者7 10.1 10.1 10.1 10.1 　
9 回答者8 100.3 100.3 100.3 　 　
1 回答者9 1000.0 1000.0 　 　 　
11 回答者10 10000.0 　 　 　 　
　 平均m 1113.8 126.5 17.3 5.4 4.6
　 標準偏差σ 3137.667 329.085 33.612 2.158 0.659
　 m+2σ 7389.143 784.625 84.486 9.716 5.934
◎　［以下の操作はすべて Microsoft Excel の中で行う］

【要点】
TRIMMEAN()ではうまく行かない．
ここでは，m+2σよりも大きな値を繰り返し削除する．
もっと統計的根拠のある方法としては，グラブスの棄却検定がある．

○　問題点：再計算と循環参照

　通常，回答者は500人以下程度，小問数は10題程度あり，目で見て手作業で削除するのは困難である．また，特定の回答者がすべての問題について極端値をとるとは限らず，極端値は虫食いのようにあちこちに散らばっている．このため，小問ごとにソートすると問題数の回数ソートし直す必要があり実用には向かない．

　考え方として，正規分布をあてはめたときにm+3σ以上の値は異質なデータと見なせることが多いが，ここで求めている所要時間については，m+2σを境目に設定する方が経験的に妥当な場合が多いので，以下m+2σを越える値を削除するものとする．（非対称な分布なので，左端のm-2σ未満となる値は負の値となり実際には起こらない．）

　この場合，Excel上で平均値と標準偏差を求める式は各々の値を参照しているので，m+2σの値に基づいて各データを削除すると循環参照となる．これを避けるところがポイント．		 実際のイメージ
(1)　「元のデータ」でm+2σを計算する．
(1)’　元のデータでm+2σを越えるのは「回答者10」なので，これを削除する．
ほとんどの回答者が4〜6秒で答えているのに，10000秒=2.8時間もかかるのは「途中でトイレに行った」「電話がかかってきた」「夕食を食べた」など何か異質な事情が入った場合が考えられる．元データのまま平均を求めると，1113.8秒という時間の9割は「回答者10」が「夕食を食べた」という事情を表わしてしまう．
(2)　残ったデータについてm+2σを計算する．
(2)’　１回削除されたデータでm+2σを越えるのは「回答者9」なので，これを削除する．

　･･･・・・

　以上のような手順を繰り返すと4回の削除で極端値がない集団となり，平均値が求められる．

　上の例2では4回削除後の平均値4.6を採用する．
※　「回答者9」「回答者8」「回答者7」は第1回検査で合格しているのに，再検査で不合格にするのか・・・何回までやるのかという疑問はありうる．
○　手順

(1)　「条件付き書式の設定」により極端値は「色で分かる」ようにしておく．
(2)　自動再計算を止めて，F・9による手動に変更する．
(3)　極端値の削除はマクロのボタンを作って行う．

以上の準備をしておき，
　　　　　　　F・9　→　マクロボタン
のように交互に４，５回繰り返し，赤字のデータが見えなくなったらできあがり．（10秒程度の作業となる．）		 (1)　列ごとに平均，標準偏差（母集団の推定値），m+2σを求めておく．
　（データにかからないように行頭数行を作業用にするとよい．他のシート上で求めると，条件付き書式の設定がやや難しくなる．）
　　　「書式」→「条件付き書式」でm+2σ超を赤で表示する．
(2)　「ツール」→「オプション」→「計算方法」で手動を選ぶ．
(3)　m+2σ超を削除するマクロを作成しボタンに登録しておく．
○　作動チェック
Microsoft Excel 2002　･･･2009.07.31･･･ＯＫ，　Microsoft Excel 2007･･･2009.07.31･･･ＯＫ
○　もっと根拠のある判断方法
　統計の参考書には「グラブスの棄却検定」という異常値判定公式があって，
　　　　　　　T=（最大値　-　平均値）/標準偏差
の値が，データの個数N=10のとき約2.0，N=100のとき約3.0よりも大きければ，その最大値は異常値と見なせるとされている．これは「１個ずつ検定」する場合には，N=10前後のときm+2σ，N=100前後のときm+3σで判断するのと同じことになるが，上で試みている方法は「同時に幾つも」検定しているので全く同じとは言えない．
(1) 「グラブス・スミルノフの棄却検定表」はExcelの組み込み関数にないので，どこかに書き込んで利用することはできる．
(2)　※に関して，グラブス検定においても何度も適用すると有意水準が甘くなるとされている．例えばα=0.025の検定を2回適用すれば，α=0.05程度まで甘くなる．
再度，常識に戻ると
　例2のデータは，10人の赤ちゃんが並んでいて体重がそれぞれ 4.0 , 4.1 , 4.3, ･･･(kg)のときに
(1)　中に10トン(10000kg)の赤ちゃんが混じっていたら　→　鯨の赤ちゃんかもしれないので除外する
(2)　次に1トン(1000kg)の赤ちゃんも大きすぎる　→　象の赤ちゃんかもしれないので除外する
･･･
というようなことは自然に分かる．微妙な判断になるのは10kgの赤ちゃんだけだと考えられる．１歳年上の赤ちゃんかもしれないし，育ちがよかったのかもしれない．
　もし，もう1人9kgの赤ちゃんが混じっていると，10kgの赤ちゃんも含めて「１歳２歳合同チームでした」ということになり，10kgは普通の値に変る．

　データが多いと極端値を「目で見つける」のは容易でないので，何らかの目安を作っておいて機械的に削除していくのがよいと考えられる．
○===ソースコード・メモに戻る
○===メニューに戻る