空間図形と三平方の定理

１
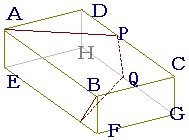
　右の図のように，AB=8cm，AD=7cm，AE=4cmの直方体ＡＢＣＤ−ＥＦＧＨがある．頂点Ａから，辺ＣＤ，ＧＨ，ＥＦ上をこの順に通って，頂点Ｂまでたるまないようにひもを巻き付け，ひもの長さが最小になるようにする．ひもが辺ＣＤ，ＧＨと交わる点をそれぞれＰ，Ｑとするとき，次の問い(1)・(2)に答えよ．
(1)　ひもが通る線を展開図にかき，ＡＰ：ＰＱを最も簡単な整数の比で答えよ．
(2)　上の直方体における線分ＡＱの長さを求めよ．
 
 
(H11年度京都府高校入試問題の引用)
■　考え方
(1)
　次の左図のように，線分ＡＢで切り開いて展開すると，展開図は右図のようになります．
ひもの長さは展開図で考えるとよいから，長さが最小となるのは，右図のようにＡ−Ｐ−Ｑ−Ｂが直線になるとき．
このとき，ＤＣ，ＨＧは平行であるから，ＡＰ：ＰＱ＝ＡＤ：ＤＨ＝［ア］：［イ］		 ア＝
イ＝
 
 


(2)
◇◇◇「直方体における線分ＡＱの長さ」は
「展開図におけるＡＱの長さ」とは異なるので注意すること◇◇◇
(1)の展開図において，AD+DH=ＨＥ＋ＥＡ＝１１ｃｍだから，Ｑはひもの真ん中で，
ＨＱ＝［ウ］ｃｍ
△ＡＤQは∠Ｄ＝９０゜の直角三角形．また，DQは三平方の定理により４√2　だから、△ADQに三平方の定理を用いて、ＡＱ＝［エ］ｃｍ
ウ＝
エ＝
 
 



《類題》　次の直方体の対角線ＡＧの長さはいくらですか．




２
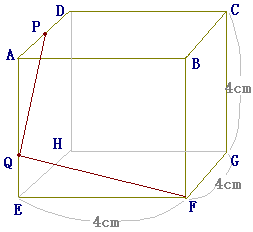
　右の図Ｉは，１辺の長さが４ｃｍの立方体ＡＢＣＤ−ＥＦＧＨで，点Ｐは辺ＡＤの中点，点Ｑは辺ＡＥ上の点です．

　また，図ＩＩは図Ｉの立方体の展開図で，この立方体のうちＡ，Ｂ，Ｅ，Ｆだけをかき入れたものです．
　このとき，次の(1),(2)の問いに答えなさい．
(1)　図ＩＩの展開図を図Ｉのように組み立てたとき，立方体の頂点Ｄにあたるところを展開図に●印でかき入れなさい．
(2)　ＰＱ＋ＱＦの長さが最小になるように点Ｑをとったとき，ＰＱ＋ＱＦの長さを求めなさい.
 
 
 
 
 

（H11年度岩手県高校入試問題の引用）
 図Ｉ

図ＩＩ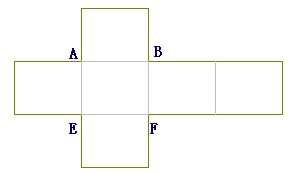
■　考え方
(1)
　立体の辺は，展開図の２か所に表示され，頂点はそれが共有されている平面の数だけ表れます．この問題では，点Ｄは展開図の３か所に現れます．
　右の図において，立方体の頂点Dにあたる所３か所を押しなさい．（途中でやり直すときはResetを押してから，やり直しなさい．）
(2)
　ＰＱ＋ＱＦの長さが最小になるのは点PＱFが一直線上にあるときです．このとき，ＰＱ＋ＱＦの長さは
 


←メニューに戻る