|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
���̕łł͈��������̉��p���Ƃ��Ď��̂S�̍��ڂ̉��������܂��D���ꂼ��̃^�C�g�����N���b�N����Ƃ��̍��ڂɃW�����v�ł��܂��D
�u�������Ⴂ�����ɂ��Đ�������v�Ƃ́C�����̒Ⴂ�P�̕����i�������Œ�̕����j�ɒ��ڂ��āC���̕����������Ƃ݂Ȃ����̕������W���i�萔�j�Ƃ݂Ȃ��Ƃ������Ƃł��D
�N�������
�u�P�����̈��������͂Q�����̈������������ȒP�v �u�Q�����̈��������͂R�����̈������������ȒP�v�u����v �Ƃ����悤�ɁC�������Ⴂ���������̕����L���ɂȂ�̂ł��D
�P�����̈��������Ȃ���̂��H�Ǝv���邩������܂��C�����Ȍ������͕ʂƂ��āC�P�����ɂ��Ă͎��́u���ʈ����ł�����v�Ƃ����ό`������܂��D
ax+bx=(a+b)x �P�����̈��������͂��ꂾ���Ȃ̂ŁC���镶���ɂ��Đ�������ƂP�����ɂȂ�����u���߂��I���ʈ����̘b���I�v�ƍl����悢���ƂɂȂ�܂��D
�y��1.1�z�@���̎��������������Ă��������D
�i����jax+bx+a2−b2 a�̎����Ƃ݂Ȃ���ax+bx+a2−b2�ƂȂ��čō����̍��͂Q���ɂȂ�܂��D b�̎����Ƃ݂Ȃ���ax+bx+a2−b2�ƂȂ��čō����̍��͂Q���ɂȂ�܂��D x�̎����Ƃ݂Ȃ���ax+bx+a2−b2�ƂȂ��čō����̍��͂P���ɂȂ�܂��D �����ŁC�������Œ�ɂȂ镶��x�ɂ��Đ�������ƗL�����Ƃ������ƂɂȂ�܂��Dx�������ƍl���C���̕����͌W���Ƃ݂Ȃ��� (ax+bx)+(a2−b2)������̂������͂P���C�E�̂������͒萔 �P�����̈��������́C���ʈ����ł�����ό`�����邾���ł�����C���ʈ������l���܂��D (a+b)x+(a+b)(a−b) =(a+b)(x+a−b)…�i���j
���̖���a�ɂ��Đ������Ă��ԈႢ�ł͂���܂��C�Q�����̈��������ɂȂ�̂Ŏ��̂悤�ɂ�╡�G�ɂȂ�܂��D
ax+bx+a2−b2 =a2+xa−b2+bx ���̂Q������������������ɂ́C�ς�−b2+bx�ɂȂ���̂����ŁC�a��x�ɂȂ���́��Ɓ���T���� (a+��)(a+��) �̌`�ɂ��܂��D �Ƃ���ŁC�ς�−b2+bx�ɂȂ���͉̂����Ƃ����ƁC����͑S�̂̑傫�Ȉ������������Ă��钆�ŁC�萔��−b2+bx���Q�̎��̐ςɕ�����Ƃ������ƂŁC�����−b2+bx�����炩���߈����������Ă����Ƃ������Ƃł��D −b2+bx=b(x−b) �����ŁCb+(x−b)=x�ƂȂ��Ęa��x�ɂȂ��Ă��܂��D ���� a2+xa−b2+bx =a2+xa+b(x−b) =(a+b)(a+x−b)…�i���j |
�y���P�z�@���̊e�����������������Ƃ��ɓ��鎮�����̑I��������I��ł��������D�i���������̂��N���b�N�j �i���ÎZ�ł͂ł��܂���D�e���v�Z�p���Ōv�Z���Ă���I������I��ł��������j x x+2 x−2 y y+2 y−2
����x�ɂ��Ă͂Q�����C����y�ɂ��Ă͂P�����ɂȂ�̂ŁCy�ɂ��Đ�������ƌv�Z���y�ɂȂ�܂��D
�i���Ӂj=(2x−4)y+(x2−3x+2) =2(x−2)y+(x−1)(x−2) ���ʈ���x−2�ł������ =(x−2)(2y+x−1) ���E��ɑ���
a+b+1
a+b−1
a−b+1
a−b−1
����a, b�ɂ��Ă͂Q�����C����c�ɂ��Ă͂P�����ɂȂ�̂ŁCc�ɂ��Đ�������ƌv�Z���y�ɂȂ�܂��D
ax+b
ax−b
bx+a
bx−a
�i���Ӂj=(a+b−1)c+(a2−2b2−ab−a+2b) ���ʈ�����T�����߂ɂ͒萔��a2−2b2−ab−a+2b�����炩���߈����������Ă����K�v������܂����C���̎���a�ɂ��Ă�b�ɂ��Ă��Q�����Ȃ̂ŁC�ǂ���Ő������Ă�����͓����ł��D�ia�ɂ��Đ�������j a2+(−b−1)a−(2b2−2b) =a2+(−b−1)a−2b(b−1) �ς�−2b(b−1)�ɂȂ���̂́C−2b, b−1�̑g��2b, −b+1�̑g�����邪�C���̂����Řa��−b−1�ɂȂ�̂�−2b, b−1�̑g a2+(−b−1)a−(2b2−2b)=(a−2b)(a+b−1) �i�����j=(a+b−1)c+(a−2b)(a+b−1) ���ʈ���a+b−1�ł������ =(a+b−1)(c+a−2b)
����a, b, x�̂ǂ̕����ɂ��Đ������Ă��Q�����Ȃ�̂ŁC���̂܂�x�ɂ��Đ�������D
a+b+c
a+b−c
a−b+c
a−b−c
�i���Ӂj=(ab)x2+(−a2−b2)x+ab x2�̌W��ab���Q�̎��̐ςɕ�����ɂ́Ca��b�̑g�Cab��1�̑g������D
������S�����ꊷ�������͕̂ʂ̈��������ɂ͂Ȃ�Ȃ��D�Ⴆ��(2x+3)(x−4)��(−2x−3)(−x+4)�͓������̂�����Cx2�̌W���𗼕��Ƃ����ɂ������͍̂l����K�v�͂Ȃ��D�i�萔���ς�邾���j
�܂��C��������ꊷ�������͕̂ʂ̈��������ɂȂ�Ȃ��D�Ⴆ��(2x+3)(x−4)��(x−4)(2x+3)�͓������̂�����C2, 1�g���l������1, 2�g���l����K�v�͂Ȃ��D ���̂悤�ɂ��Đς�ab�ƂȂ�Q�̐���a,b�̑g�Cab,1�̑g�����ׂ���悢�D 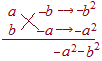 �萔����ab���Q�̎��̐ςɕ�����ɂ́Ca��b�̑g�Cab��1�̑g������D
�萔����ab���Q�̎��̐ςɕ�����ɂ́Ca��b�̑g�Cab��1�̑g������D�����̑g�������������|�����������ōl����ƁC�E�}�̑g��x�̂P���̌W������v����D ���̐}��(ax−b)(bx−a)�̏ȗ��ł��邩�� (ax−b)(bx−a)…�i���j
�����ӂ����āu���ꂢ�Ȋ|���Z�̌`�����Ă��邩��v�������łɈ��������ł��Ă���̂ł͂Ȃ����ƍl���Ă���l�͗���s�\���ł��D���������́u��ԑ傫�ȋ�肪�ς̌`�ɂȂ��Ă��Ȃ���Ȃ�Ȃ��v�̂ɑ��āC���̖��̍��ӂ� (a−b)(c−b)(c+a)−abc �Ƃ����`�Łu��ԑ傫�ȋ�肪�����Z�v�ɂȂ��Ă���̂ŁC�܂����������͂ł��Ă��܂���D �ł͂ǂ�����Ĉ�����������̂��Ƃ����ƁC�܂��W�J���Ď��̐�������n�߂邵���Ȃ��̂ł��D ����a, b, c�̂ǂ̕����ɂ��Đ������Ă��Q�����ɂȂ�̂ŁCa�ɂ��ēW�J���Đ�������D (a−b)(c−b)(c+a)−abc=(c−b)(a−b)(a+c)−bca =(c−b)(a2+(c−b)a−bc)−bca =(c−b)a2+(c−b)2a−bc(c−b)−bca =(c−b)a2+{(c−b)2−bc}a−bc(c−b) a2�̌W��c−b���Q�̎��̐ςɕ�����ɂ́Cc−b��1�̑g�����ł��D�܂��C�萔��−bc(c−b)���Q�̎��̐ςɕ�����ɂ́C−bc ,c−b�g�Cbc ,−(c−b)�g�Ȃǂ�����D 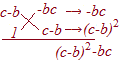 �����̑g�����̓��ŁCa��1���̌W����(c−b)2−bc�ɂȂ���̂��������|�����������ōl����ƁC�E�}�̂悤�ɂȂ�D
�����̑g�����̓��ŁCa��1���̌W����(c−b)2−bc�ɂȂ���̂��������|�����������ōl����ƁC�E�}�̂悤�ɂȂ�D���̐}��((c−b)a−bc)(a+(c−b))�̏ȗ��ł��邩�� (ca−ab−bc)(a−b+c)…�i���j |