■閉曲線で囲まれた図形の面積
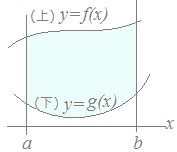【基本】右図のような図形の面積は， S={ f(x)−g(x) }dx で求められます． 
円x2+y2=4の方程式をyについて解くと， y=± となるので，この円の面積は S={ −(−) }dx =2dx で求められますが，右の解説のように，結果は4πになります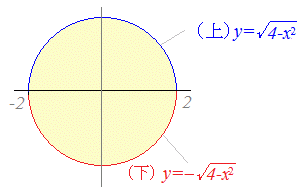．  閉曲線2x2−2xy+y2=4によって囲まれた図形の面積 y2−2xy+(2x2−4)=0を解の公式を用いてyについて解くと y=x±=x± となる．
4−x2≧0から定義域は−2≦x≦2
この閉曲線で囲まれた図形の面積は
S={ (x+)−(x−) }dx
=2dx=4π
となって，【例１】と同じになります．
グラフは，y=xに半円y=を足したもの，及び引いたものだから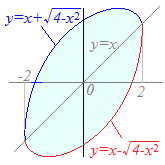 
計算上はxが差し引きで消えてしまうせいです．
図形上は，（上）：x+も（下）：x−も と−から同じ分量xだけ持ち上げているので，面積は元の円と等しいということになります． |
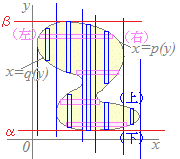 （参考）左で述べた S={ f(x)−g(x) }dx は，絶対的なものではありません．右図のように縦に切ると幾つもの区間に場合分けしなければならず，横に切れば場合分けが簡単になるときは x=の形に解きなおして，右（大きい方）をx=p(y)，左（小さい方）をx=q(y)すると， S={ p(y)−q(y) }dy で求められます． 【例１】の円では，縦に切っても横に切っても切り口は２本の線になるので，よく使う縦に切る方法で解説しています．
【図で考えると楽になる計算…半円の面積】
（参考）…置換積分によって上記の(1)を計算する方法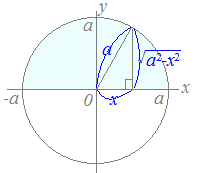
定数a>0のとき，
dx…(1)
をていねいに計算しようとすると，下記の参考のような計算を行うことになり，この変形を毎回行うのは大変です．図で考えると，(1)は右図のような半円の面積を表しており dx= とすることができます．
なお，この計算がこのように簡単になるのは，積分区間が−a≦x≦aという形で，「半円の全部」になっている場合であることに注意してください．
dx
のような場合は，これほど簡単にはなりません．
変形の要点
I=dxを計算するために
x=asintとおけば1−sin2t=cos2tだから cost>0のとき，=costとなることに目を付けると x=asintと置けば =acostとなって，根号がはずれます．
−≦t≦のときcost>0だから I=a2cos2tdt=a2dt= |
||||||||
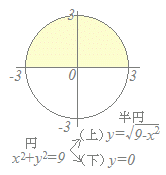右図のような半円の面積が
dx
だから，…（答）
置換積分を用いて厳密にていねいに計算してもできるが，（解き方が指定されていなければ）図を見て簡単に求めてもよい．
|
|||||||||
|
y2−4xy+(5x2−4)=0を解の公式を用いてyについて解くと y=2x±=2x± (−2≦x≦2) となる．
4−x2≧0から定義域は−2≦x≦2
この閉曲線で囲まれた図形の面積は
S={ (2x+)−(2x−) }dx
=2dx
となって，【例１】と同様に，原点を中心とする半径2の円の面積だから4πになります．
|
|||||||||
|
y2+2xy+(2x2−1)=0を解の公式を用いてyについて解くと y=−x± (−1≦x≦1) となる．
1−x2≧0から定義域は−1≦x≦1
この閉曲線で囲まれた図形の面積は
S={ (−x+)−(−x−) }dx
=2dx
となって，原点を中心とする半径1の円の面積だからπになります．
|
|||||||||
|
【例３】 S=dx のように，xの項を含む場合は，平方完成により S=dx =dx =dx と変形すると
x−1=tとおく置換積分により
S=dtとなって，
原点を中心とする半径3の上半円の面積になるから
S=と求められます．
|
【例４】 S=dx (a>0) のように，x2の項に係数が付いている場合は S=adx と変形することにより，左の【例３】と同様に（半）円の面積と結びつけることができます．
S=dxを求めるには
S=2dx=2dx
=2dx
=2dx
x+1=tとおく置換積分により
S=2dt=π
|
||||||||
|
dx=dx
=dx=dx=Iとおく
x−3=tとおくと置換積分により
I=dt（半径2の円の上半分だから）=2π
|
|||||||||
|
y2+2xy+(5x2−16x+12)=0を解の公式を用いてyについて解くと，y=−x±=−x±2 定義域は，−x2+4x−3≧0から1≦x≦3 この閉曲線で囲まれた図形の面積は S={ (−x+2)−(−x−2) }dx =4dx=4dx =4dx=4dx
x−2=tとおくと置換積分により
4dx=4dt
となって，原点を中心とする半径1の半円の面積×4=2πになります．
|
|||||||||
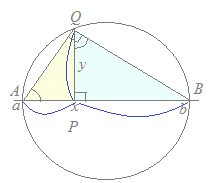 （図形的な意味）次の図において ∠AQB=90°, △APQ∽△QPB → AP:PQ=PQ:PBとなることから (x−a):y=y:(b−x) y= になり，与えられた積分はx=a, x=bを直径の両端とする半円の面積になります． 半径r=の半円の面積になるから S=π()2=(b−a)2 |
（式の変形だけで示すには，かなり長い変形を要します･･･以下は要点）
S=dx
とおき，根号内を平方完成します． (x−a)(b−x)=−x2+(a+b)x−ab=−{x2−(a+b)x}−ab =−{(x−)2−()2}−ab=−(x−)2+()2 ここで =p , =r とおくと
S=dx
x−p=tの置換積分により
S=dt
となって，半径r=の半円の面積になるから
S=π()2=(b−a)2
|
＝＞［作者］：連絡ありがとう．-1≦x≦-3ということはありません（-1が-3よりも小さい［以下］ということはない）．左図のようになりますので，元の答案で正しいです．2次不等式の解き方があなたの弱点ですので簡単に復習しておくとよいでしょう．