|
== 合成関数 == ■解説 ○ 合成関数とは x → u → y のように対応しているとき( u が x の関数で,y が u の関数になっているとき),x から y への対応を考えることができる.
関数 g(x) の x の代わりに関数 f(x) を代入したものを g(f(x)) で表わし,f と g の合成関数といい,g
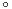 f で表わす. f で表わす.( f と g の合成関数というとき,g(f(x)) すなわち g 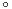 f を表わす.[記号の順序とは逆で対応の順序,x →f(x)→ u →g(u)→ y と一致]) f を表わす.[記号の順序とは逆で対応の順序,x →f(x)→ u →g(u)→ y と一致])
g(f(x)) は (g 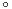 f)(x) とも書かれる. f)(x) とも書かれる.
(※初歩的) 関数の合成と関数の積とは別のものである. 例 f(x)=x+1 , g(x)=2x のとき, 関数の積 f(x)g(x)=(x+1)(2x)=2x2+2x 関数の合成 f(g(x))=2x+1 関数の合成 g(f(x))=2(x+1)=2x+2 (※初歩的) x が複数個あるような関数と合成するときは,それら全部を関数に置き換える. 例 f(x)=x2+x , g(x)=3x のとき, f(g(x))=(3x)2+(3x)=9x2+3x
1. g(f(x)) と f(g(x)) とは一般に異なるものとなる.すなわち
関数の合成について,交換法則は(常には)成り立たない. 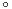 g≠g g≠g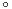 f f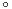 (g (g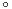 h)=(f h)=(f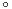 g) g)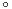 h h |
 y=2u+1のとき, - - - - - - - - - - - - - - - - y=2(3x2)+1 f(x)=3x2 , g(x)=2x+1 のとき, g(f(x))=2(3x2)+1 例2 f(x)=sinx , g(x)=2x のとき, f(g(x))=sin( 2x) g(f(x))=2sin x 例3 f(x)= , g(x)= のとき, f(g(x))= g(f(x))= 例4 f(x)=x2+x+1 , g(x)=x+2 のとき, (f  g)(x)=(x+2)2+(x+2)+1=x2+5x+7 g)(x)=(x+2)2+(x+2)+1=x2+5x+7(g  f)(x)=(x2+x+1)+2=x2+x+3 f)(x)=(x2+x+1)+2=x2+x+3 |
||