[解説]
2次の正方行列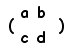 については,は次の関係式がつねに成り立ちます。これをケーリー・ハミルトンの定理といいます。
A2-(a+d)A+(ad−bc)E=0 については,は次の関係式がつねに成り立ちます。これをケーリー・ハミルトンの定理といいます。
A2-(a+d)A+(ad−bc)E=0
[応用]
|
A2 → (a+d)A-(ad−bc)E
とみると,左辺は2次,右辺は1次
つまり,次数を下げる変形ができます。 |
行列のn乗を変形するのに用いることができます:
例
A=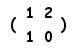 のとき, のとき,
a+d=1,ad−bc=-2だから,
A2-A-2E=0
これを用いれば,
A2=A+2E
両辺にAをかけて,
A3=A2+2A=(A+2E)+2A=3A+2E=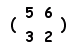 同様にして,
同様にして,
A4=A3A=(3A+2E)A=3A2+2A
=3(A+2E)+2A=5A+6E=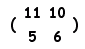
などと変形できます。 |
※ 証明は,成分計算を気長に行えばできます。
A=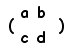 のとき, のとき,
A2-(a+d)A+(ad−bc)E
=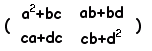 + +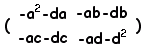
+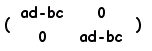 = =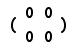
※ 行列の計算は2つの処理方法があります。
1 成分で行う方法(何でもできるが,遅い)
2 行列で行う方法(使えるところは速い)
ケーリー・ハミルトンの"定理自身"は上記のように成分計算で示しますが,ひとたびこの定理が証明できると,ケーリー・ハミルトンの定理を用いた行列での変形が可能となります。[行列は行列でやる。]
ただし,ケーリー・ハミルトンの定理で何でもできるわけではないので,行き詰まれば成分計算を併用します。
[要点]--計算の方針--
使えるところは,新幹線(ケーリー・ハミルトン)で行く,
残りは,普通列車(成分計算)で行く。 |
|