|
[要点] ある不等式(A)が成り立つことを数学的帰納法によって証明するには,次のようにすればよい. (I) n=1 のとき(A)が成り立つことを証明する. (II) n=k のとき(A)が成り立つことを仮定する. その仮定を使って n=k+1 のとき(A)が成り立つことを証明する. [例題1]
n が 3 以上の整数のとき,次の不等式が成り立つことを証明せよ.
[証明]
2n>2n …(A)
(I) n=3 のとき, 左辺=23=8 右辺=6 よって,n=3のとき(A)が成り立つ. (II) n=k ( k≧3 )のとき(A)が成立すると仮定すれば,
2k>2k …(B)
(B)の両辺に 2 を掛けると
どこからそんな話が出てくるのか?それは,n=k+1 のときの左辺の形を予想すると,式(B)と ×2 の分だけ違うからである.
2k×2>2k×2
2k+1>4k
次に 4k と 2(k+1) を比較すると ※
4k−2(k+1)=2k−2=2(k−1)>0 ( k≧3 だから)
よって,
2k+1>4k>2(k+1) ※
2k+1>2(k+1)
したがって,n=k+1 のときも(A)が成立する.(I),(II) より, 3 以上のすべての正の整数 n について(A)が成り立つ.
勢い余って「すべての正の整数について成立する」などと書かないように.「 3 以上」だけでしか成り立たないことに注意
|
[不等式の証明で注意すべき点] 左辺と右辺が等しくないのが不等式なので,ほとんどの場合左辺を変形していっても右辺にはならない. ※において 4k を変形しても 2(k+1) にはならない. 証明したいことは 2k+1>2(k+1) だから,この結論に合うように 4k>2(k+1) を証明すればよい.
このように,不等式の証明問題では左辺から得られる不等式を変形しているだけでは本来の結論までたどり着かないことが多いので,「結論との間につなぎを入れる」ことが重要である.
具体的には※のように「差を作って大小比較する」とよい. n=k のときと n=k+1 のときを比較すると 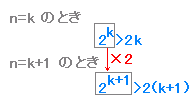 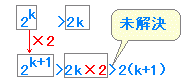 ※この問題では「右辺からすり寄って」「左辺を比較する」やりかたでもできるが少し複雑になる. (B)の両辺に 2 を加えると
2k+2>2k+2=2(k+1)
次に
2k+1−(2k+2)=2k(2−1)−2=2k−2
ここで k≧3 だから
2k−2≧8−2=6>0
よって
2k+1>2k+2>2k+2=2(k+1)
|
|
[例題2]
n が 4 よりも大きい自然数のとき,次の不等式が成り立つことを証明せよ.
[証明]
2n>n2 …(A)
(I) n=5 のとき, (*1) 左辺=25=32 右辺=52=25 よって,n=5 のとき(A)が成り立つ. (II) n=k ( k≧5 )のとき(A)が成立すると仮定すれば,
2k>k2 …(B)
(B)の両辺に 2 を掛けると
2k+1>2k2
次に
2k2−(k+1)2
k≧5 のとき
=k2−2k−1 =(k−1)2−2 (*2)
(k−1)2−2≧14>0 (*3)
よって,n=k+1 のときも(A)が成立する.(I),(II) より,4 よりも大きい自然数 n について(A)が成り立つ. |
(*1) 4 よりも大きい自然数だから n は 5 以上 (*2) 2次関数の最小値を求めたいのだから,平方完成して頂点の座標を求める.
(II) において次のように書いている答案は零点なので要注意
n=k のとき
2k>k2
n=k+1 のとき
2k+1>(k+1)2
⇒ n=k のときも,n=k+1 のときも代入しているだけで何も証明されていない.n=k+1 のときも代入してしまうと,その式が n=k+1 のときに成立することを仮定していることになる.⇒ n=k のときは成立することを仮定しなければならないが,n=k+1 のときは成立することを証明しなければならない. (*3) k≧5 という条件を使わなければ (k−1)2−2>0 は示せない. この範囲外,たとえば k=1 のときは (k−1)2−2=−2<0 となり,証明はできない. |
|
[例題3]
n が 2 以上の自然数のとき,次の不等式が成り立つことを証明せよ.
1+ + + ··· + > …(A)
[証明](I) n=2 のとき,
左辺=1+ = =1.5
右辺= ==1.33...
よって,n=2 のとき(A)が成り立つ.(II) n=k ( k≧2 )のとき(A)が成立すると仮定すれば,
1+ + + ··· + > …(B)
(B)の両辺に を加えると
1+ + + ··· + + > + =
次に
−
= { (2k+1)(k+2)−2(k+1)(k+1) }
= { 2k2+5k+2−(2k2+4k+2) }
= > 0 (∵ k≧2 )
したがって
1+ + + ··· + + > >
よって,n=k+1 のときも(A)が成立する.(I),(II) より,2 以上のすべての自然数 n について(A)が成り立つ. |
[例題4]
n が 2 以上の自然数のとき,次の不等式が成り立つことを証明せよ.
[証明]
+ + + ··· + < 2− …(A)
(I) n=2 のとき,
左辺= + = 1+ =
右辺=2− = =
よって,n=2 のとき(A)が成り立つ.(II) n=k ( k≧2 )のとき(A)が成立すると仮定すれば,
+ + + ··· + < 2− …(B)
(B)の両辺に を加えると
+ + + ··· + + < 2− +
次に
2− > 2− + を証明する.
(2− )−(2− + )
=− + −
= { -k(k+1)+(k+1)2−k }
= { -k2−k+k2+2k+1−k }
= > 0 (∵ k≧2 )
したがって
+ + + ··· + + < 2− +
< 2−
よって,n=k+1 のときも(A)が成立する.(I),(II) より,2 以上のすべての自然数 n について(A)が成り立つ. |
|
[問題]
すべての自然数 n について,次の不等式が成り立つことを証明せよ.
4n > 3n …(A)
※初めに [ ? ] で示される空欄を1つ選び,続いてその空欄に入る値を右の選択肢から1つ選べ.
[証明](I) n=1 のとき,
左辺=[ ? ]
右辺=[ ? ]
よって,n=1 のとき(A)が成り立つ.(II) n=k のとき(A)が成立すると仮定すれば,
4k > 3k …(B)
(B)の両辺に [ ? ] を掛けると
4k+1 > [ ? ] k
次に
したがって,
4k+1 > 12k > 3(k+1)
よって,n=k+1 のときも(A)が成立する.(I),(II) より,すべての自然数 n について(A)が成り立つ. |
[選択肢]
|