|
以下において，位相の異なる瞬時値をベクトルの記号，などで表すものとする．
【RLC並列回路】
○ 次の図のように，抵抗R，コイルL，コンデンサCが交流電源に並列に接続されているときに流れる電流は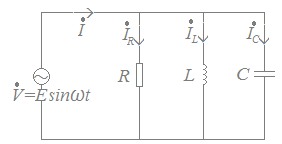 
(1) R, L, Cに加わる電圧は等しい．
が成り立つことを用いて求めることができます．(2) 電流の瞬時値は，各電流 , , の和に等しい． （なお，各電流は位相が異なるので，Iの実効値は各電流の実効値の和にはなりません．）
= = =
= + +
= sin ωt+ sin(ωt−)+Cω E sin(ωt+)
○ 右図のように
sin(ωt+)=−sin(ωt−)
で，とは逆向きだから
= sin ωt+ sin(ωt−)−Cω E sin(ωt−)
= sin ωt+(−Cω E)sin(ωt−)
IRを基準方向として右向きに描き，IL −ICを下向きに描くと，次の図の水色の直角三角形の斜辺の長さが電流Iの大きさを表すことになる．
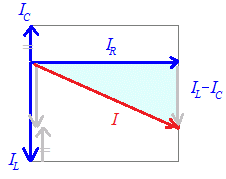
電流の大きさは
I=
また，インピーダンスは次の赤で示した部分だから
電圧と電流の位相差（遅れ）をθで表すと tanθ=
= sin ωt+ sin(ωt−)− sin(ωt−)
=E{ sin ωt+(−)sin(ωt−) }
インピーダンスの大きさは
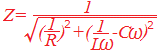 インピーダンスと電圧との位相差（遅れ）をθで表すと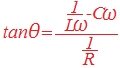 
|
【交流における抵抗，コイル，コンデンサの働き】
※詳細は，【→この頁】を見てください．
○１ 抵抗Rに流れる電流は，その両端に加わる電圧と同じ位相になる．（抵抗は正弦波交流の位相を変えない）
=E sin ωtのとき
○２ コイルLに流れる電流の位相は，その両端に加わる電圧の位相よりも遅れる．= sin ωtになる （コイルは正弦波交流の位相を遅らせる．）
=E sin ωtのとき
○３ コンデンサCに流れる電流の位相は，その両端に加わる電圧の位相よりも進む．= sin(ωt−)になる （コンデンサは正弦波交流の位相を進める．）
=E sin ωtのとき
=Cω E sin(ωt+)になる 図１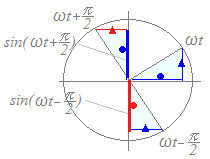 
sin(ωt−)=−sin(ωt+)
sin(ωt+)=−sin(ωt−)
|
|
［問題１］
図１に示す，R[Ω]の抵抗，インダクタンスL[H]のコイル，静電容量C[F]のコンデンサからなる並列回路がある。この回路に角周波数ω[rad/s]の交流電圧[V]を加えたところ,この回路に流れる電流[A]，[A]，[A]，[A]のベクトル図が図２に示すようになった。このとき，LとCの関係を表す式として，正しいのは次のうちどれか。 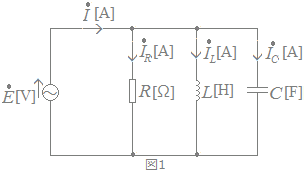 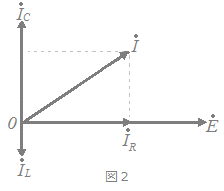 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成19年度「理論」問9 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
IC>IL
だから
CωE>
Lω>
なお，(3)と(4)は同じ内容．(5)は無関係．(1)(2)のうちで(2)が正しい．
→【答】(2)
|
|
［問題２］
図１のように，R[Ω]の抵抗，インダクタンスL[H]のコイル及び静電容量C[F]のコンデンサを並列に接続した回路がある。この回路に正弦波交流電圧e[V]を加えたとき，この回路の各素子に流れる電流iR[A]，iL[A]，iC[A]とe[V]の時間変化はそれぞれ図２のようで，それぞれの電流の波高値は10[A]，15[A]，5[A]であった。回路に流れる電流i[A]の電圧e[V]に対する位相として，正しいのは次のうちどれか。  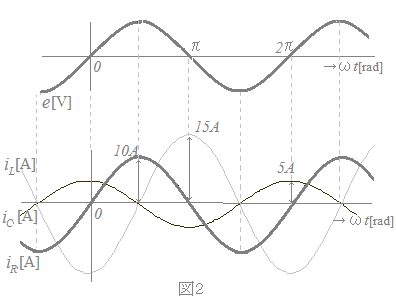 (4) 45°進む (5) 90°遅れる HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成15年度「理論」問8 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
iL=15sin(ωt−)
iC=5sin(ωt+)=−5sin(ωt−)
だから，iLとiCは一部相殺しあって，合計
iL&iC=10sin(ωt−)
の遅れ位相となる．抵抗に流れる電流は
iR=10sin(ωt)
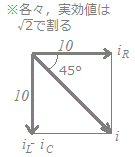だから，右図により45°遅れる．
→【答】(3)
|
|
［問題３］
図のように，R1=20[Ω]とR2=30[Ω]の抵抗，静電容量C=[F]のコンデンサ，インダクタンスL=[H]のコイルからなる回路に周波数f[Hz]で実効値V[V]が一定の交流電圧を加えた。f=10[Hz]のときにR1を流れる電流をI10Hz[A]，f=10[MHz]のときにR1を流れる電流をI10MHz[A]とする。このとき，電流比の値として，最も近いものを次の(1)〜(5)のうちから一つ選べ。 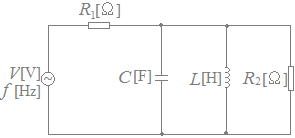 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成24年度「理論」問10 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
インピーダンスは
Z=R1+
R1=20, R2=30, C=, L=だから （ア）f=10[Hz]，ω=2π×10[rad/s]のとき
==0.2
Cω==0.2
−Cω=0 だから
Z=R1+R2=50[Ω]
I10Hz=[A]
（イ）f=10[MHz]=107[Hz]，ω=2π×107[rad/s]のときインピーダンスの第二項の分母の根号内において
()2=≒0.001
=≒2×10−7=0.0000002
Cω==0.02×106=20000
したがって，根号内はほとんどCωの大きさで決まり，他は全く影響しない．
根号内=(Cω)2=200002
インピーダンスの第二項は
≒=0.00005
したがって，インピーダンスは
Z=20.00005≒20[Ω]
I10MHz=[A]
ゆえに
==0.4
→【答】(1)
|
|
［問題４］
図のようなRLC交流回路がある。この回路に正弦波交流電圧E=100[V]を加えたとき，可変抵抗R[Ω]に流れる電流I[A]は零であった。また，可変抵抗R[Ω]の値を変えてもI[A]の値に変化はなかった。このとき，容量性リアクタンスXC[Ω]の端子電圧V[V]とこれに流れる電流IC[A]の値として，正しいものを組み合わせたのは次のうちどれか。 ただし，誘導性リアクタンスXL=20[Ω]とする。 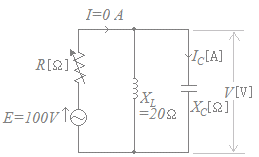 電圧V[V]電流IC[A]
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成14年度「理論」問8 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
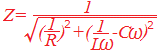もしも，可変抵抗Rも並列に接続されているのならば，右のインピーダンスの式は有限の値となり，電流は流れ，零となるようなことはありません． しかし，この問題ではL, Cだけが並列に接続されており，この部分についてはRの項がありません． （直列接続されているRは，並列接続の部分を求めてから，後で考えると分かりやすいでしょう．） L, Cの並列部分については， 「インピーダンスの分母が形式的に０ ⇒ インピーダンスが∞ ⇒ 電流が流れない」ということがあります． −Cω=0 のときに，これが起ります． このことは，並列回路において電流を表す式（Rの項がないとき）
= sin ωt+E(−Cω) sin(ωt−)
において
−Cω=0
のとき，つねに=0となることからも分かります．（このとき，L, Cの内部では，電流が互いに逆向きに流れていて，共振が起っていますが，その外側には電流は流れないことになります．）
E=100[V] （実効値は100[V]）
だからLω=20[Ω] 電圧は
E=100[V] （実効値はV=100[V]）
電流は
=5=ECω
その実効値は
IL=IC=5[A]
→【答】(3)
|
...メニューに戻る