|
【sin xの微分積分と位相の遅れ,進み】
(解説)○ sin xを微分すると,位相を進めるのと同じになります.
(sin x)=sin(x+)
○ sin xを積分すると,(定数項を別として)位相を遅らすのと同じになります.
sin x dx=sin(x−)+C
○ 高校の数学Ⅲで習う三角関数の微分公式によれば,
(sin x)=cos x
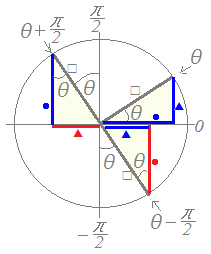
です.ところで,数学Ⅱで習う三角関数の相互関係として,右図1中で角度θ+に対応する円周上の点のy座標は●だから
sin(θ+)==cosθ
すなわち
cos x=sin(x+)
したがって
(sin x)=sin(x+)
になり,微分することは,位相を進めるのと同じになります.○ 高校の数学Ⅲで習う三角関数の微分公式によれば,
sin x dx= −cos x+C
です.ところで,数学Ⅱで習う三角関数の相互関係として,右図1中で角度θ−すなわち−+θに対応する円周上の点のy座標は●だから
sin(θ−)==−cosθ
すなわち
−cos x=sin(x−)
したがって
sin x dx=sin(x−)+C
になり,積分することは,位相を遅らせるのと同じになります.
右へ続く→
|
図1
 →続き xに係数aが付いているときは
(sin ax)=a cos ax
だから
(sin ax)=a sin(ax+)
また,積分の方は
sin ax dx= −cos ax+C
だから
sin ax dx=sin(ax−)+C
※ 正弦波交流でよく登場するように変数をtで表し,角速度をωで表すと,これらの公式は次の形にまとめることができます.
(sin ωt)=ω sin(ωt+) …(*1)
⇒ 微分するかわりに,「角速度を掛けて,位相を進める」とよい.
sin ωt dt=sin(ωt−)+C …(*2)
⇒ 積分するかわりに,「角速度で割って,位相を遅らせる」とよい.
|
|
|
【交流における抵抗,コイル,コンデンサの働き】
(解説)○1 抵抗Rに流れる電流Iは,その両端に加わる電圧Vと同じ位相になる. (抵抗は正弦波交流の位相を変えない)
V=E sin ωtのとき
○2 コイルLに流れる電流Iの位相は,その両端に加わる電圧Vの位相よりも遅れる.I= sin ωtになる (コイルは正弦波交流の位相を遅らせる.)
V=E sin ωtのとき
○3 コンデンサCに流れる電流Iの位相は,その両端に加わる電圧Vの位相よりも進む.I= sin(ωt−)になる (コンデンサは正弦波交流の位相を進める.)
V=E sin ωtのとき
I=Cω E sin(ωt+)になる ○1 R[Ω]の抵抗にV[V]の電圧がかかるとき,オームの法則により
V=IR
が成り立つから,
E sin ωt=IR
I= sin ωt
になります.(黒字は定数)○2 コイルに電流が流れると,回路には「電流の変化率」に比例する逆向きの起電力がかかります.これを自己誘導といい,その比例定数Lは,自己誘導係数と呼ばれ,各々のコイルごとに,その巻数,面積,長さ,回路中の媒質の透磁率によって定まる定数となっています.(単位はヘンリー[H]) 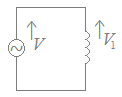
V1=−L
キルヒホフの第2法則(閉回路の起電力の和は電圧降下の和に等しい)により,次の関係式が成り立ちます.
V−L=0
E sin ωt−L=0
したがって
=sin ωt (黒字は定数)
両辺をtで積分すると
I=sin ωt dt=cos ωt+C
上で検討したように,この式は
I=sin(ωt−)+C
と書けます.ここで,積分定数Cの値について,次のグラフで考えてみます. C>0の場合は,平均して正の向きに電流が流れることになり,図の水色で示したような直流成分のまわりを振動していることになりますが,このようなことにはなりません.C<0の場合も同様にして,図の桃色で示したような負の向きの直流成分のまわりを振動していることとなり,このようなことにもなりません.実際の交流では,真中のグラフのようにC=0のまわりを振動するようになっています. 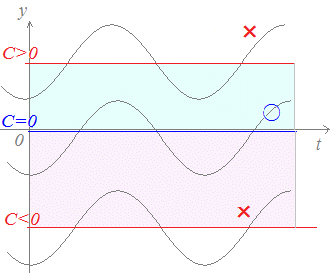
I=sin(ωt−)
(別解)I=I0sin(ωt+α)の形の解を求める.(定数I0とαを求める)
E sin ωt−L=0
に代入すると
E sin ωt−LωI0cos(ωt+α)=0
これより
E=LωI0 …(1)
(1)から
sin ωt=cos(ωt+α) …(2)
I0=
(2)から(cosx=sin(x+)に注意すると)
sin ωt=sin(ωt+α+)
よって,(一般にsinα=sinβとなるのは,α=βの場合だけでなく,他にもいろいろあるが,ここでは1つ見つければよいから,簡単にα=βとする.)
ωt=ωt+α+
α=−
以上により
I=sin(ωt−)
|
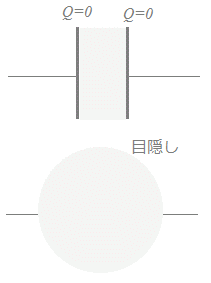
○3 初めに,コンデンサについては,次の重要な事実を確かめておく必要があります.
コンデンサには直流は流れないが,交流は流れる.
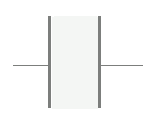 コンデンサの極板間は,空気や誘電体などの絶縁体で満たされており,「極板間を電流が流れることはありません」.
コンデンサの極板間は,空気や誘電体などの絶縁体で満たされており,「極板間を電流が流れることはありません」.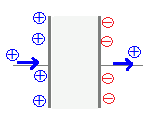 回路につながれているコンデンサでは,導線を通じて電荷が運ばれてきて電極に蓄えられます.(陰極では,電荷0の状態から電荷が流れ出て,結果的に負になると考えます.)
回路につながれているコンデンサでは,導線を通じて電荷が運ばれてきて電極に蓄えられます.(陰極では,電荷0の状態から電荷が流れ出て,結果的に負になると考えます.)
右図の[Next→]ボタンを繰り返し押して,電荷が出入りする様子を見てください.そのとき,コンデンサに目隠しをした下の図では「左から電荷が流れ込んで右に出て行く」「右から電荷が流れ込んで左に出て行く」ように見えることを確かめてください. 極板間には電流が流れませんが,極板に電荷が蓄えられたり,極板から電荷が出て行ったりすると,導線には電気が流れているのは本当であり,全体として右向きに又は左向きに流れるというのは本当です. - - - - 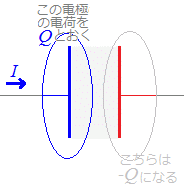 方程式を立てる際に,まず,コンデンサの1つの極板の電荷をQとおくとき,回路を流れる電流Iは電荷Qの単位時間当たりの増分であることに注意しましょう. 方程式を立てる際に,まず,コンデンサの1つの極板の電荷をQとおくとき,回路を流れる電流Iは電荷Qの単位時間当たりの増分であることに注意しましょう.
【重要】
この関係式において,I>0のときは,蓄えられた電荷Qが増える方向に電流が流れ,I<0のときは,Qが減少します.…電気量の微分が電流
I= …(3)
次に,コンデンサの電気量と電圧に関する次の基本公式も思い出しましょう.
「オバQはシブイ」
Q=CV …(4)
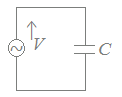 右図のような回路において,V=E sin ωtの交流電圧がかかるとき,回路に流れる電流を求めるものとする.
右図のような回路において,V=E sin ωtの交流電圧がかかるとき,回路に流れる電流を求めるものとする.(4)の両辺を微分すると
=C=C(E sin ωt)
左辺に(3)を,右辺に(*1)を適用すると
I=Cω E sin(ωt+)
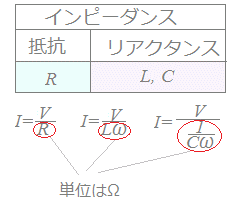 ○ 以上の結果をまとめて考えるときに,オームの法則における抵抗に相当するものが,各々どんな形をしているかを覚えておきます.
○ 以上の結果をまとめて考えるときに,オームの法則における抵抗に相当するものが,各々どんな形をしているかを覚えておきます.ただし,Rだけのときは単純に抵抗と呼ばれ,Rを含まないL又はC(もしくはその両方)のときはリアクタンス,RとL又はC(もしくはその両方)のときはインピーダンスと呼ばれますが,いずれも単位はΩ(オーム)になります. Lだけのとき,XLで表し,誘導性リアクタンスとも呼ばれます. Cだけのとき,XCで表し,容量性リアクタンスとも呼ばれます. ○ また,交流は正弦波の瞬間値V=E sin ωtで表されるだけでなく,ベクトル(電磁気学では上にドットを付けて表す)で表されることが多い. 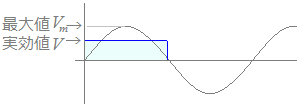
V=
の関係があり,V=Vm sin(ωt+θ)のことを
=V∠θ
と書く.【例】 V=141sin(ωt+)すなわちVm=141(≒)[V],θ=のとき
=100∠
と書く.○ 電流についても同様にI=Im sin(ωt+θ)のことを
=I∠θ
と書く.【例】 I=141sin(ωt−)すなわちIm=141(≒)[A],θ=−のとき
=100∠−
と書く. |
|
【RLC直列回路のインピーダンスと位相】 交流電源に対してRLCが直列に接続されている回路における電流の大きさ,位相を求めるには,上記の性質を使ってベクトル合成して求めます.
試験会場で微分方程式を解いていたのでは間に合いませんので,上記の結果を使って以下に述べるような図を描いて解くようにします.
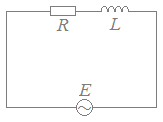 RL直列回路
RL直列回路Rは電源電圧の位相を変えないので,基準方向(右向き)に描きます. Lは電源電圧に対して電流の位相を90°遅らせる働きがあるので,基準方向から反時計回りに90°のベクトルで(上向きに)表します. 合成したベクトルの大きさがインピーダンスの大きさを表し,基準方向となす角が電流の位相を表します. 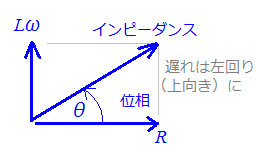 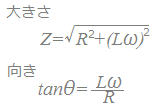 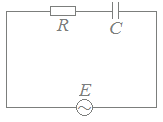 RC直列回路
RC直列回路Rは電源電圧の位相を変えないので,基準方向(右向き)に描きます. Cは電源電圧に対して電流の位相を90°進める働きがあるので,基準方向から時計回りに90°のベクトルで(下向きに)表します. 合成したベクトルの大きさがインピーダンスの大きさを表し,基準方向となす角が電流の位相を表します. 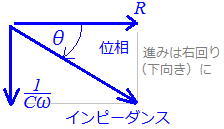 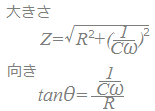
【例題】
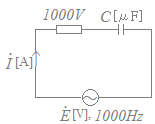 図のように,1000[Ω]の抵抗と静電容量C[μF]のコンデンサを直列に接続した交流回路がある。いま,電源の周波数が1000[Hz]のとき,電源電圧[V]と電流[A]の位相差は[rad]であった。このとき,コンデンサの静電容量C[μF]の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
図のように,1000[Ω]の抵抗と静電容量C[μF]のコンデンサを直列に接続した交流回路がある。いま,電源の周波数が1000[Hz]のとき,電源電圧[V]と電流[A]の位相差は[rad]であった。このとき,コンデンサの静電容量C[μF]の値として,最も近いものを次の(1)~(5)のうちから一つ選べ。
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成23年度「理論」問9 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. 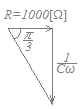 (解説)
(解説)右図により,
=1000
ω=2π×1000=6283[Hz]
だから
C==9.19×10−8
=0.092×10−6[F]=0.092[μF] →(2)
|
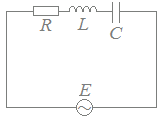 RLC直列回路
RLC直列回路Rは電源電圧の位相を変えないので,基準方向(右向き)に描きます. Lは電源電圧に対して電流の位相を90°遅らせる働きがあるので,基準方向から反時計回りに90°のベクトルで(上向きに)表します. Cは電源電圧に対して電流の位相を90°進める働きがあるので,基準方向から時計回りに90°のベクトルで(下向きに)表します. まず,LとCとで差をとって,これとRを合成します. 合成したベクトルの大きさがインピーダンスの大きさを表し,基準方向となす角が電流の位相を表します. 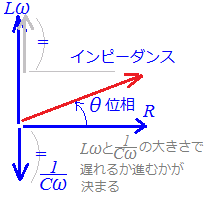 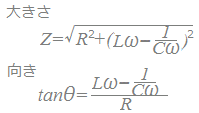 R=0のとき 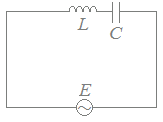 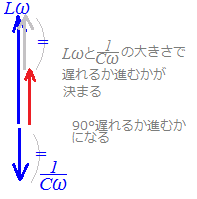 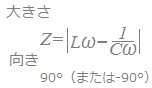 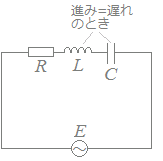 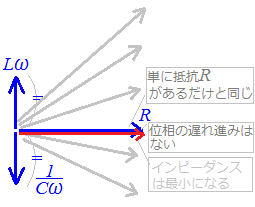
Lω=となる周波数を共振周波数と言います.
共振周波数のとき,インピーダンスは抵抗だけがあるのと同じことになり,インピーダンスの大きさは最小となります.
|
|
[問題1]
図に示したように,R[Ω]の抵抗とインダクタンスL[Ω]のコイルを直列に接続した回路がある。この回路に角周波数ω[rad/s]の正弦波交流電圧[V]を加えたとき,この電圧の位相[rad]に対して回路を流れる電流[A]の位相[rad]として,正しいのは次のうちどれか。 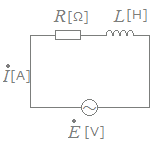 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成18年度「理論」問9 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
角速度ω[rad/s]は角周波数と呼ばれることもあります.
逆三角関数の表す意味は各々次の通り. sin−1x=θはarcsin x=θとも書かれ,sinθ=xとなる角θを表す.(ただし,−≦θ≦ とする.) cos−1x=θはarccos x=θとも書かれ,cosθ=xとなる角θを表す.(ただし,0≦θ≦πとする.) tan−1x=θはarctan x=θとも書かれ,tanθ=xとなる角θを表す.(ただし,−≦θ≦ とする.) 
tanθ= すなわち θ=tan−1
だけ遅れる.
→【答】(5)
|
|
[問題2]
図1のような抵抗R[Ω]と誘導性リアクタンスX[Ω]との直列回路がある。この回路に正弦波交流電圧E=100[V]を加えたとき,回路に流れる電流は10[A]であった。この回路に図2のように,更に抵抗11[Ω]を直列接続したところ,回路に流れる電流は5[A]になった。抵抗R[Ω]の値として,最も近いのは次のうちどれか。 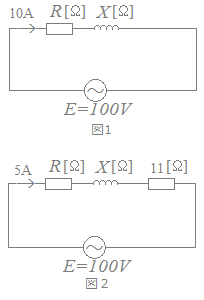 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成16年度「理論」問8 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
Z=を使います. 図1については,
==10 → R2+(Lω)2=100 …(1)
図2については,
==20 → (R+11)2+(Lω)2=400 …(2)
(2)よりR2+22R+121+(Lω)2=400 …(2’)(2’)−(1)
R2+22R+121+(Lω)2=400
− ) R2+(Lω)2=100
22R+121=300
22R=179
R=8.13...
→【答】(2)
|
|
[問題3]
図のように,静電容量Cx[F]及びC[F]のコンデンサとインダクタンスL[H]のコイルを直列に接続した交流回路がある。この回路において,スイッチSを開いたときの共振周波数はf1[Hz],閉じたときの共振周波数はf2[Hz]である。f1[Hz] がf2[Hz]の2倍であるとき,静電容量の比の値として, 正しいのは次のうちどれか。 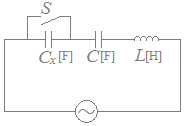 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成17年度「理論」問8 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
スイッチSを開いたとき,直列接続された2つのコンデンサの合成容量は
Lω1= …(1)
スイッチSを閉じたときは,コンデンサCxにかかる電圧は0になり,回路に影響しなくなる.このときの角速度をω2とおくと
Lω2= …(2)
(1)(2)より
ω12=
ω22=
仮定により,共振周波数f1=2πω1, f2=2πω2について
f1:f2=ω1:ω2=2:1だから
よって
ω12:ω22=4:1
=
Cx+C=4Cx
3Cx=C
=3
→【答】(5)
|
|
[問題4]
図のように,R=200[Ω]の抵抗,インダクタンスL=2[mH]のコイル,静電容量C=0.8[μF]のコンデンサを直列に接続した交流回路がある。この回路において,電源電圧[V]と電流[A]とが同位相であるとき,この電源電圧の角周波数ω[rad/s]の値として,正しいのは次のうちどれか。 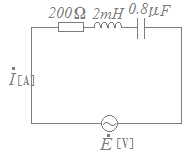 (4) 2.5×104 (5) 3.5×104 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成18年度「理論」問7 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
※角速度は角振動数とも呼ばれます.
電源電圧と電流とが同位相になるのは
Lω=
のときだから,
2.0×10−3ω=
ω2==
ω==0.25×105=2.5×104
→【答】(4)
|
|
[問題5]
次の文章は,RLC直列共振回路に関する記述である。
R[Ω]の抵抗,インダクタンスL[H]のコイル,静電容量C[F]のコンデンサを直列に接続した回路がある。 この回路に交流電圧を加え,その周波数を変化させると,特定の周波数fr[Hz]のときに誘導性リアクタンス=2πfrL[Ω]と容量性リアクタンス=[Ω]の大きさが等しくなり,その作用が互いに打ち消し合って回路のインピーダンスが(ア)なり,(イ)電流が流れるようになる。この現象を直列共振といい,このときの周波数fr[Hz]をその回路の共振周波数という。 回路のリアクタンスは共振周波数frより低い周波数では(ウ)となり,電圧より位相が(エ)電流が流れる。また,共振周波数fr[Hz]より高い周波数では(オ)となり,電圧より位相が(カ)電流が流れる。 上記の記述中の空白箇所(ア),(イ),(ウ),(エ),(オ)及び(カ)に当てはまる組合せとして,正しいものを次の(1)~(5)のうちから一つ選べ。 (ア)(イ)(ウ)(エ)(オ)(カ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成24年度「理論」問7 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |

Lω=となる周波数を共振周波数と言います.
○ 図のように,共振周波数に等しいとき,インピーダンスは抵抗だけがあるのと同じことになり,インピーダンスの大きさは最小となります.(ただし,ω=2πfr)→ (ア)小さく,(イ)大きな ○ ω’<ω=2πfrのときは
Lω’<Lω=<となるからが勝ることになる.
→ (ウ)容量性,(エ)進んだ○ ω’>ω=2πfrのときは
Lω’>Lω=>となるからLω’が勝ることになる.
→ (オ)誘導性,(カ)遅れた→【答】(3)
|
|
[問題6]
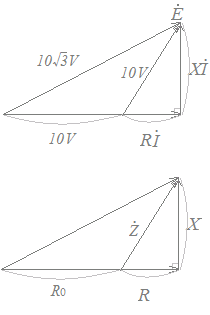
図1のように,抵抗R0=16[Ω],インピーダンス[Ω]の誘導性負荷(抵抗R[Ω],誘導性リアクタンスX[Ω])を直列に接続した交流回路がある。正弦波交流電圧=10[V]の電源をこの回路に接続したところ,R0の端子間電圧の大きさ,誘導性負荷の端子間電圧の大きさは,それぞれ10[V]であった.次の(a)及び(b)に答えよ。 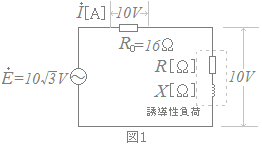 の関係をベクトル図で表すと図2のようになる。電流[A]の大きさの値と,電圧と電流の位相差θ[°]の値として,正しいものを組み合わせたのは次のうちどれか。 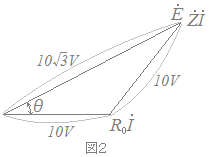 電流[A]の大きさ位相差θ[°]
HELP(b),(R0+R),の関係をベクトル図で表すと図3のようになる。これより,R[Ω]とX[Ω]の値として,最も近いものを組み合わせたのは次のうちどれか。 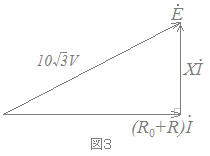 R[Ω]X[Ω]
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成15年度「理論」問16 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
(a)
R0=16=10だから
=0.625
右の2つの図は相似図形で上の図は下の図を倍したものである.上の図において,三平方の定理を使って2つの未知数R, Xの満たす連立方程式を作り,これを解くことを考える.
(R)2+(X)2=102…(1)
(10+R)2+(X)2=(10)2…(2)
(2)より
100+20R+(R)2+(X)2=300…(2’)
(2’)−(1)
100+20R=200
(1)に代入
20R=100 R=5
52+(X)2=102
このとき
(X)2=75 X=5
tanθ====
θ=30°
 →【答】(4)
(b)
R0:R=10:5=2:1だから
さらに
R=8[Ω]
R:X=1:だから
X=8=13.856...[Ω] →【答】(2)
|
|
[問題7]
図のように,R=ωL[Ω]の抵抗,インダクタンスL[H]のコイル,スイッチSが角周波数ω[rad/s]の交流電圧[V]の電源に接続されている。スイッチSを開いているとき,コイルを流れる電流の大きさをI1[A],電源電圧に対する電流の位相差をθ1[°]とする。また,スイッチSを閉じているとき,コイルを流れる電流の大きさをI2[A],電源電圧に対する電流の位相差をθ2[°]とする。このとき,及び|θ1−θ2|の値として,正しいものを組み合わせたのは次のうちどれか。 
|θ1−θ2|
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成21年度「理論」問8 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
スイッチが開いているとき
Z====2ωL
I1=
スイッチが閉じているとき
I2=
したがって
=
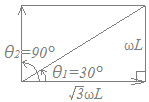 位相については右図から
位相については右図から
|θ1−θ2|=60°
→【答】(2)
|