.

■Rコマンダーによる主成分分析

○主成分分析とは，この頁の目標
　主成分分析の概要については，【この頁】を参照
　Rコマンダーを用いると主成分分析が簡単にできてしまうので，表面的な理解に流れるのを防ぐためにここでは次の２点に焦点を当てて少し掘り下げてみる．
  1. 主成分の個数を何個にすればよいか
  2. 各主成分にはどのような名前を付ければよいか
※主成分分析では，複数の変数に座標変換を行って，不偏分散が最大となるような新変数（主成分）を作る．そのとき元の変数ｎ個で表わされる情報を幾つかの主成分に要約して表し，累積寄与率がそこそこ大きくなるところまで主成分の個数を増やしていく．


図1

○Rコマンダーにおける主成分分析の操作手順

　初めに，主成分分析に用いるデータの例を【この頁】からExcelに取り込んでおくとよい．これにより保存されたExcelファイルのいずれかのシートに，以下において利用するデータが保存されてるものとする．（日本語２バイト文字のフォルダ名，ファイル名は使用しない方がよい．）
  1. Rを起動する．(*1)
  2. Rコマンダーを起動する．(*2)
  3. 上記のExcelデータをインポートする．
  4. 【以下はRコマンダーのメニューで行う】データ→データのインポート→ExcelまたはAccess，dBaseのデータセットから
  5. データセット名はそのままでよい
  6. フォルダ，ファイル名を指定して開く．→シートを選ぶ．（ここで［データセットを表示］して確かめておくとよい．）
  7. 【以下はRコマンダーのメニューによる主成分分析】統計量→次元解析→主成分分析
  8. 項目1から項目10までのすべての変数を選び［相関行列の分析］［スクリープロット］にチェックを入れる．→OK
    ※［相関行列の分析］にチェックを入れないと，以下に述べるカイザー基準は利用できない．
  9. 右図3のようなグラフが得られる．また，出力ウィンドウには表1のように出力される．

Excel2002のとき
(*1)　RExcel→Start　R
(*2)　RExcel→RComannder→with separate menus

Excel2007のとき
(*1)(*2)ともアドインからスタートする．
図2


図3

表1
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
3.649 1.956 1.367 0.981 0.701
Comp.6 Comp.7 Comp.8 Comp.9 Comp.10
0.547 0.342 0.238 0.136 0.084
Importance of components:　　　　　
　 Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 1.910 1.399 1.169 0.990 0.837
Proportion of Variance 0.365 0.196 0.137 0.098 0.070
Cumulative Proportion 0.365 0.560 0.697 0.795 0.865
　 Comp.6 Comp.7 Comp .8 Comp. 9 Comp.10
Standard deviation 0.739 0.585 0.488 0.368 0.290
Proportion of Variance 0.055 0.034 0.024 0.014 0.008
Cumulative Proportion 0.920 0.954 0.978 0.992 1.000


○主成分分析における主成分の個数の決め方

　次のいずれかの基準で決めるのがよいとされている．
  1. 累積寄与率が70%あるいは80%程度になるように選ぶ．
  2. カイザー基準による．
  3. スクリープロット基準による．
　表1においてStandard deviationは標準偏差，その２乗が分散Varianceになる．この例では変数の個数が10個なので標準化データの分散の和は10になるので，各々の分散の割合（proportion）は10で割った数字になっている．
　Cumulative Proportionが累積寄与率を表している．
  1. 累積寄与率を見ると第3主成分までで69.7%，第4成分までで79.5%になる．
  2. カイザー基準で考えると，表1において１よりも大きいのは第3主成分までになる．
  3. 一般の場合にはもっとはっきりとエルボーが分かるが，図3の場合は第3主成分ないしは第4主成分までと考えざるを得ない．
以上により，カイザー基準が判断しやすいのでこれにより第3主成分までとする.．
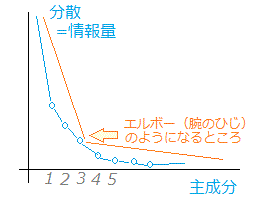
1.　図1のイメージで考えるたとき，全体の分散のうち７，８割の情報が集約できればよいと考える．完全に（100%）の情報を集約しようとすると主成分の個数が多くなり過ぎて元と変わらず，うれしくない．

2.　カイザー基準とは，元のデータを標準化したデータ（相関行列から分析したとき）を用いたときに利用できる基準．この場合には，全体の分散が「変数の個数」に等しくなり，各変数の分散が「固有値の大きさ」に等しくなることを利用する．主成分に情報を集約しているのだから元の変数１個分以上となる主成分を採用するというのがカイザー基準．

3.　各主成分(component)の分散（variance）を棒グラフにすると図3のようになる．（折れ線グラフで表すことが多い．）このとき次の図のようにエルボーができた所よりも先には情報が少ないので，エルボーまでの主成分を採用するという考え方．


図4

○主成分の命名
　表2のような係数が出力されている．（10は機械的にソートされて１の次に表示されている．負の値はたまたま逆向きのベクトルになっただけでその絶対値に意味がある．）

　第1主成分では項目２，５，７，９が大きい．これらは，下水道普及率，小学校教員１人当たり小学校児童数，人口千人当たり刑法犯認知件数，一人当たり県民所得の影響の大きさを表しているから，筆者は「都市型」と名付けたのであるが読者によっては他の見方があるかもしれない．

　第2主成分では，項目10，４，６，８と項目２，３の影響が大きい．これらは，人口１人当たり個人預貯金残高，主要道路舗装率，交通事故死傷者数，人口10万人当たり一般病院数および下水道普及率，コンビニエンスストア数の影響を表しているから筆者は「自動車型」と名付けたのであるが読者によっては他の見方があるかもしれない．

　第３主成分では，項目１，2、１０および項目4の影響が強いことを表している．これらは，持ち家住宅の延べ面積，下水道普及率，個人預貯金残高および主要道路舗装率の影響を表している．筆者はこれだけでは分からないので，元のデータで項目１，１０，９，４をソートしてその上位・下位に位置する県名を参考にすることにした．（表３）
　核家族化の度合いとか工業化の度合いなどに関係しているのかもしれないが，第１主成分および第２主成分と無相関な都道府県力を持ってこなければならない（主成分は互いに独立であることを要す）ので，よくわからない．		 表２
　 Comp.1 Comp.2 Comp.3
項目１ 0.274 -0.184 -0.549
項目１０ -0.224 0.314 -0.583
項目２ -0.357 -0.373 0.123
項目３ -0.132 -0.457 0.158
項目４ -0.188 0.430 0.347
項目５ -0.479 -0.076 0.108
項目６ -0.127 0.398 -0.092
項目７ -0.434 0.196 0.055
項目８ 0.293 0.363 0.234
項目９ -0.418 0.000 -0.347

表３
項目１ 項目１０ 項目２ 項目４
東 京 都 東 京 都 東 京 都 千 葉 県
神奈川県 香 川 県 神奈川県 宮 崎 県
大 阪 府 徳 島 県 大 阪 府 香 川 県
沖 縄 県 和歌山県 北 海 道 佐 賀 県
埼 玉 県 大 阪 府 兵 庫 県 熊 本 県
･･･ ･･･ ･･･ ･･･
新 潟 県 福 島 県 佐 賀 県 長 崎 県
石 川 県 鹿児島県 島 根 県 青 森 県
山 形 県 青 森 県 高 知 県 富 山 県
福 井 県 宮 崎 県 和歌山県 山 形 県
富 山 県 沖 縄 県 徳 島 県 岩 手 県

...メニューに戻る　..Rのメニューに戻る