【類題3.3】
原点 O(0, 0, 0)を通り,直線  \( \displaystyle \frac{x-4}{2}=\frac{y+ 3}{3}=z-2 \) \( \displaystyle \frac{x-4}{2}=\frac{y+ 3}{3}=z-2 \)を含む平面の方程式を求めてください.
解答1を見る解答1を隠す
A.[高校数学の範囲で解く場合]
《3点を通る平面の方程式》として解く
直線 ) \( \displaystyle \frac{x-4}{2}=\frac{y+ 3}{3}=z-2(=t) \) \( \displaystyle \frac{x-4}{2}=\frac{y+ 3}{3}=z-2(=t) \)上から2つの点を選び,原点と合わせて3つの点を通る平面の方程式として求める
) \( \displaystyle \frac{x-4}{2}=\frac{y+3}{3}=z-2(=t) \) \( \displaystyle \frac{x-4}{2}=\frac{y+3}{3}=z-2(=t) \)において,
t=0, 1を代入すると, (4, −3, 2), (6, 0, 3)
そこで,3点 O(0, 0, 0), A(4, −3, 2), B(6, 0, 3)を通る平面の方程式を
ax+by+cz+d=0とおき,係数 a, b, c, dを求める(定数倍を除いて定める)
(見やすくまとめる)
 d=0
d=0…(1)
4a−3b+2c=0…(2')
2a+c=0…(3')
↓ d=0だから d以外の1文字( a≠0)を媒介変数として表す
 d=0
d=0…(1)
c=−2a…(3")
4a−3b+2(−2a)=0…(2")
原点 Oを通るから
d=0…(1)
点 A(4, −3, 2)を通るから
4a−3b+2c+d=0…(2)
点 B(6, 0, 3)を通るから
6a+3c+d=0…(3)
b=0, c=−2a, d=0
平面の方程式は
ax−2az=0( a≠0)
したがって, x−2z=0…(答)
B.[高校数学の範囲で解く場合]
《1点と平面上の2つのベクトルから求める問題》として解く
直線の方向ベクトル ) \( \displaystyle \vec{u}=(2,3,1) \) \( \displaystyle \vec{u}=(2,3,1) \)は求める平面に含まれる.さらに,原点
O(0, 0, 0)とこの直線上の点 A(4, −3, 2)を結ぶベクトル
) \( \displaystyle \vec{u}=(2,3,1) \) \( \displaystyle \vec{u}=(2,3,1) \)も平面に含まれる.
そこで,原点 O(0, 0, 0)を通り,2つのベクトル
) \( \displaystyle \vec{u}=(2,3,1) \) \( \displaystyle \vec{u}=(2,3,1) \),
) \( \displaystyle \vec{v}=(4,-2,3) \) \( \displaystyle \vec{v}=(4,-2,3) \)によって張られる平面の方程式として求める.
2つの媒介変数 s, tを用いて,次の形に書ける
(x, y, z)=s(2, 3, 1)+t(4, −3, 2)
↑↓
 x=2s+4t
x=2s+4t…(1)
y=3s−3t…(2)
z=s+2t…(3)
↓
(3)より s=z−2tとして,(1)(2)の sを消去する
x=2(z−2t)+4t=2z…(1')
y=3(z−2t)−3t=3z−9t…(2')
↓
x=2z( yは任意の値)…(答)
【類題3.4】
2点 A(1, 2, 3), B(1, 0, 1)を通り,平面 x+y+z+1=0に垂直な平面の方程式を求めてください.
解答1を見る解答1を隠す
2つの平面のなす角は,それぞれの法線ベクトルのなす角に等しい(ただし,高校では0°〜90°で答える.)
平面 x+y+z+1=0の法線ベクトルを, ) \( \displaystyle \vec{n_1}=(1,1,1) \) \( \displaystyle \vec{n_1}=(1,1,1) \),
2点 ABを結ぶベクトルを ) \( \displaystyle \overrightarrow{\rm{AB}}=(0,-2,-2) \) \( \displaystyle \overrightarrow{\rm{AB}}=(0,-2,-2) \),求める平面の法線ベクトルを
) \( \displaystyle \vec{n}=(a,b,c) \) \( \displaystyle \vec{n}=(a,b,c) \)とおくと
 \( \displaystyle \vec{n}\perp\overrightarrow{\rm{AB}} \) \( \displaystyle \vec{n}\perp\overrightarrow{\rm{AB}} \)により
−2b−2c=0…(1)
 \( \displaystyle \vec{n}\perp\vec{n_1} \) \( \displaystyle \vec{n}\perp\vec{n_1} \)により
a+b+c=0…(2)
(1)(2)より
a=0, b=−c
=c(0,-1,1)) \( \displaystyle \vec{n}=(0,-c,c)=c(0,-1,1) \) \( \displaystyle \vec{n}=(0,-c,c)=c(0,-1,1) \)
求める平面の法線ベクトルは, (0, −1, 1)とおける.
点 A(1, 2, 3)を通り法線ベクトル (0, −1, 1)に垂直な平面の方程式は
0(x−0)−1(y−2)+1(z−3)=0
−y+z−1=0
y−z+1=0…(答)
求める平面の方程式を ax+by+cz+d=0とおくと
A(1, 2, 3)を通るから
a+2b+3c+d=0…(1)
B(1, 0, 1)を通るから
a+c+d=0…(2)
平面 x+y+z+1=0の法線ベクトル ) \( \displaystyle \vec{n_1}=(1,1,1) \) \( \displaystyle \vec{n_1}=(1,1,1) \)と平面 ax+by+cz+d=0の法線ベクトル
) \( \displaystyle \vec{n}=(a,b,c) \) \( \displaystyle \vec{n}=(a,b,c) \)は垂直だから
a+b+c=0…(3)
(1)(2)(3)から a,b,cを d(≠0)で表すと
a=0, b=d, c=−d
平面の方程式は
dy−dz+d=0 (d≠0)
y−z+1=0…(答)
|
 (解説)
(解説)


 右図においてPHを含む平面が
右図においてPHを含む平面が

 2つの平面が交わるとき,2平面のなす角 \(\theta\) は各々の法線ベクトルのなす角 \(\lambda\) に等しい.
2つの平面が交わるとき,2平面のなす角 \(\theta\) は各々の法線ベクトルのなす角 \(\lambda\) に等しい.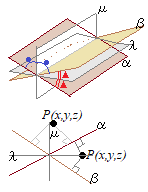 2平面
2平面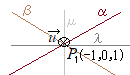 (参考)
(参考)