|
■Excelを用いた度数分布表の作成[3] ピボットテーブル ■ はじめに 以下においては、右の表1〜表3のような生データを集計して、表1A〜表3Aのような度数分布表を作成する方法を解説します。(「データの個数」を「度数」といいます。) 生データは、表1では「バス」のような文字データ、表2では「2」のような整数の数値データ、表3では「175.1」のような実数(小数)の数値データとして与えられており、各々数十から数千程度の件数が表計算ソフト上に入力されているものとします。 数十件程度のデータならば「手作業(=目で数えて)」でも集計はできますが、数千件程度となると手作業ではミスが多くなり、点検にも時間がかかりますので、表計算ソフトを用いて短時間に・正確に数えて「表1A〜表3Aのような度数分布表に仕上げる」方法を考えます。 ここでは、ほとんどのパソコンにインストールされているMicrosoft Excelのピボットテーブルを用いて度数分布表を作成する方法を解説します。操作画面はExcel2007で解説します。(他のバージョンでもほとんど同じです。) ■ ピボットテーブルの長所 Excelのピボットテーブルを利用すると
(1) 表1のようにデータが「バス」のような文字列である場合でも度数分布表を簡単に作成することができます。特に、好きなスポーツ、余暇の過ごし方のような自由記述式アンケートの集計などにおいてどのようなデータが登場するかあらかじめ予想できない場合や表記の異なるデータが登場する場合などにおいても楽に対応できます。 (2) 表2のような整数の数値データ、表3のような実数の数値データから度数分布表を作成する(さらにヒストグラムを作成する)ことも簡単にできます。 (3) ピボットテーブルを利用するときは、COUNTIF()ではあらかじめ準備しなければならなかった値の一覧表やFRWQUENCY()であらかじめ作成しておかなければならなかった階級表(区切り値の表)は必要なく、ツールから自動的に出力されます。ただし、元のデータが書き換えられたとき、ピボットテーブルの出力結果は自動的には追随しません。データ範囲が変更されない限り(データの追加・削除がなければ)、「!」アイコンを利用することにより更新することはできます。) |
表1表2表3
   表1A表2A表3A
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
■ ピボットテーブルを利用した度数分布表の作成 (I) 文字列データからの度数分布表の作成 下の表4のような文字列データ(B列が文字列)からピボットテーブルを利用して度数分布表を作成するには(以下、Excel2007で解説。Excel2002の場合は下記)
(1) データテーブル(下図ではA1からB51までの範囲)のどこかをポイントしておく。この段階でポイントしていないときは、(2)の操作の後に行う。
表4
(2) メインメニューで「挿入」→「ピボットテーブル」を選択する。 (3) (1)の操作を行っていれば、データテーブルの途中に空白行、空白列がない限りデータの下端・右端までの連続した範囲が自動的に「テーブルまたは範囲」として入力される。 (4) 下図5のようにそのワークシート内で右下方向にデータがない範囲を選択して「既存のワークシート」に出力するようにすると、何度も練習したときにワークシートが増え過ぎることはない。→OKボタンをクリック (5) 下図6にように生徒番号(行見出しに使用しているデータ)は選択せず、通学手段だけを選択→ピボットテーブルが一部できてくる (6) 右図7にように右上の欄から通学手段をつかんでテーブルの右下の欄までドラッグ (7) この例のように生データが文字列データとなっている場合には、ピボットテーブルの左上の欄は「データの個数」だけが利用可能となる。右図8のようにできあがる。  
※ Excel2002の場合(青字がExcel2007との相違点)は
(1) データテーブルのどこかをポイントしておく。この段階でポイントしていないときは、(2)の操作の後に行う。
(2) メインメニューで「データ」→「ピボットテーブルとピボットグラフ レポート」を選択する。→Excelのリスト/データベース、ピボットテーブルを選択して[次へ] (3) (1)の操作を行っていれば、データテーブルの途中に空白行、空白列がない限りデータの下端・右端までの連続した範囲が自動的に「テーブルまたは範囲」として入力される。 (4) そのワークシート内で右下方向にデータがない範囲を選択して「既存のワークシート」に出力するようにすると、何度も練習したときにワークシートが増え過ぎることはない。→OKボタンをクリック (5) 右図9にように通学手段だけを選択→「行のフィールドを・・・」と書かれた欄へドラッグ。「データアイテムを・・・」と書かれた欄へも同じものをドラッグ (6) 上のExcel2007の場合と同様にできあがる。 |
図6
  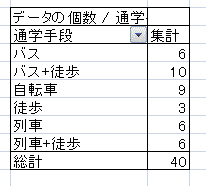 図9  |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(II) 整数の数値データからの度数分布表の作成 右図10のような整数の数値データからピボットテーブルを使って度数分布表を作成する場合は、上記の文字列データとほぼ同じ方法で行うことができます。 出典:気象庁統計資料、1951年から2010年までのわが国における年ごとの台風上陸数 ホーム > 気象統計情報 > 天気予報・台風 > 過去の台風資料 > 台風の統計資料 > 台風の上陸数 : http://www.data.jma.go.jp/fcd/yoho/typhoon/statistics/landing/landing.html
整数の数値データの場合に文字列データと異なる点は、ピボットテーブルを作成したときに、右上の欄でデータとして「年間(台風上陸数)」を選択したときに、右図11のように初め「合計」が表示される点です。
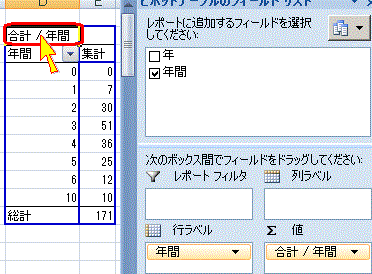
求めたいものは「年間上陸数を行ラベル」として集計した「データの個数」なので、その目的に合うように次のように変形します。 (*) 右図12のようにピボットテーブルのフールドリストと書かれた欄から「年間」の項目を行ラベルへドラッグします。 (**) 右図13→図14のようにピボットテーブルの左上欄をダブルクリックして「データの個数」を選択します。→OK
※ Excel2002の場合(Excel2007との相違点)は
(*) メインメニューで「データ」→「ピボットテーブルとピボットグラフ レポート」を選択する。→Excelのリスト/データベース、ピボットテーブルを選択して[次へ]
図10
(*) 「年間」を「行のフィールドを・・・」と書かれた欄と「データアイテムを・・・」と書かれた欄の両方へドラッグ  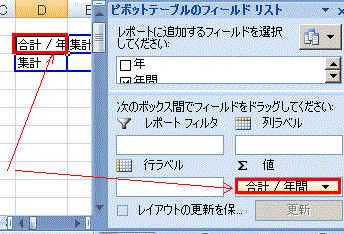 |
図12
   |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(III) 実数の数値データからの度数分布表の作成
(はじめに)
もし、あなたが「次のような疑問」を持っているとすれば、あなたは数学的に非常に見通しの良い方です・・・「そもそも、実数の数値からなるデータについて、階級の区切り値も示さずに度数分布表を作ると、(理論上実数値には等しいものはまずないから)各々1個ずつという自明な結果となって、意味がないのではないか? 実際、Excelのピボットテーブルを使って実数の数値データから度数分布表を作ると右図15のようになり(全部異なる値が小さいものから順に並ぶだけだから)各々1人ずつという自明な結果が得られ、あなたの洞察が素晴らしかったことが示されます。 しかし、Excelでは一旦この場面になってから「身長の区分のグループ化」を行うことができ、この表を「度数分布表」に変えることができるのです。 右図15のような50人の生徒の身長データがあり、小数第1位まで測定されているものとします。このデータから、「155.0(cm)以上160.0(cm)未満」「160.0(cm)以上165.0(cm)未満」・・・のように5(cm)間隔に階級を設定して度数分布表を作るには
【要点】
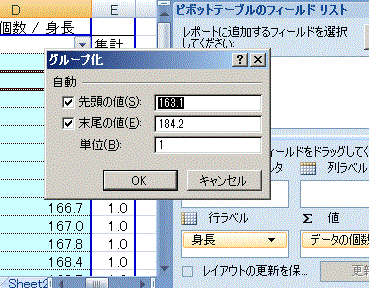
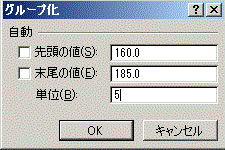
○ ピボットテーブルを作ってから、行見出しを右クリックして「グループ化」する。 ○ 階級幅は次の図のように設定する。 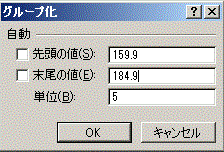 【詳細】 (*) はじめの操作は、整数の数値データから成る場合と同じ:
(1) データテーブル(図15ではA1からB51までの範囲)のどこかをポイントしておく。この段階でポイントしていないときは、(2)の操作の後に行う。
図15
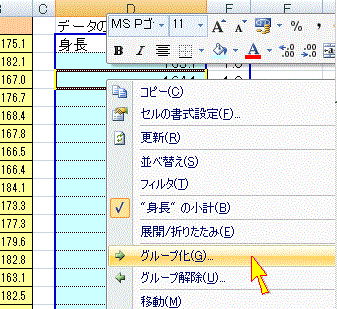
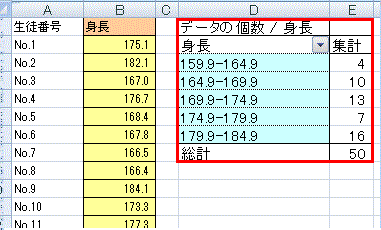
(2) メインメニューで「挿入」→「ピボットテーブル」を選択する。 (3) (1)の操作を行っていれば、データテーブルの途中に空白行、空白列がない限りデータの下端・右端までの連続した範囲が自動的に「テーブルまたは範囲」として入力される。 (4) そのワークシート内で右下方向にデータがない範囲を選択して「既存のワークシート」に出力するようにすると、何度も練習したときにワークシートが増え過ぎることはない。→OKボタンをクリック (5) 生徒番号(行見出しに使用しているデータ)は選択せず、通学手段だけを選択→ピボットテーブルが一部できてくる。(しかし、この段階では右図16のように「身長の合計」などという欲しくもない項目が1つできるだけで、まだ度数分布表として目指す形にはなっていない。) (6) 右図17のようにピボットテーブルのフールドリストと書かれた欄から「身長」の項目を行ラベルへドラッグします。 (7) 右図18のように同じデータが2つ並んだ変な集計表になっています。(数値のデータをピボットテーブルに掛けると初め「合計」になるが、各データがほとんど1つずつしかないから、値と合計が一致します。) (8) まず、合計ではなく「データの個数」に変更するために、ピボットテーブルの左上端をダブルクリックします。(右図19)→(右図20) (これで上記の図15で予想した通りに、各データ1個ずつ(たまたま一致するデータがあっても2個くらい)という分布表になります。) (9) ここから、「身長の区分のグループ化」を行います。 まず、図21のように、ピボットテーブルの行見出しとなっている身長の欄を「右クリック」します。 (10) 図22のようにグループ化を選択します。 (11) 図23のダイアログボックスで設定するグループ化においては、FREQUENCY()関数の利用のときと同様に、指定した区切り値が160.0<x≦165.0のように「…より大…以下」型で使われることに注意します。 すなわち、図24のように設定すると、先頭の値のチェックは外して(最小値を区切りの下端に使うことはやめる)、160.0から5.0の階級幅で185.0まで区切っていくという設定になります。(初めに登場したダイアログボックスに最小値(先頭の値)と最大値(末尾の値)が見えているから、それらの間を5.0ずつ区切っていけばよいと考える) 図24の書き方は、「先頭の値」「末尾の値」のチェックを外すこと、「単位」(=階級幅)を5.0にすることについては正しい操作ですが、160.0から185.0という値が間違っています。この設定では、160.0<x≦165.0,165.0<x≦170.0,… 180.0<x≦185.0の幅に区切られて、日本の常識となっている「…以上…未満」型になりません。 (165.000000000のような高精度な測定を行うときに165.000000000のような区切り値それ自体が登場する可能性はまずありませんが、通常の身長、体重測定のように小数第1位までの測定では165.0のように区切り値自体が登場することがあります。この値を160.0<x≦165.0 に含めてしまうと160.0≦x<165.0とは書けないことになります。) 図25のように区切りたい値よりも0.1だけ小さい小数を使うと、「…以上…未満」型にすることができます。(このデータでは、例えば159.91のような小数第2位までの実数は登場しないから) (12) OKボタンをクリックすればできあがりです。(図26) ※この図26においては、「ある階級で一番大きな値」が「次の階級で一番小さい値」となって重複して登場していることに注意してください。この表では159.9<x≦164.9,164.9<x≦169.9,… 179.9<x≦184.9 を表しています。レポートなどにまとめるときは、値が重複するような書き方は避けて、出来上がった表の「値のコピー」を作ってから、160.0- , 165.0- , … 180.0- などと書き直す方がよいでしょう。 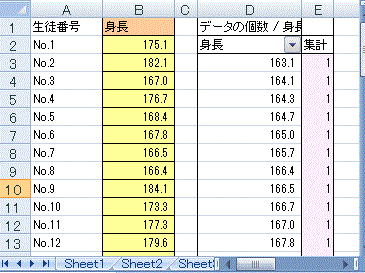  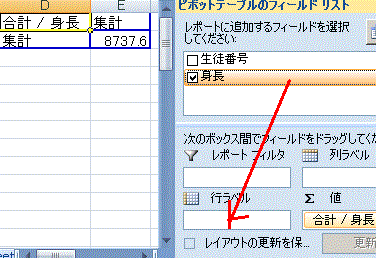 |
図18
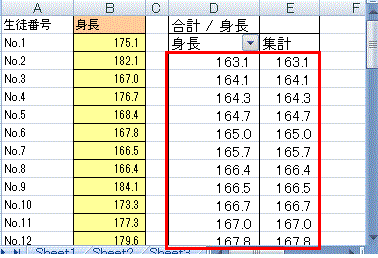         ※Excel202の場合、数値データのときの操作上の相違点は(II)で述べた通り。グループ化と区切り値の設定はExcel2007の場合と同じです。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
≪練習用の問題≫ 次のデータから度数分布表を作ってください。 (表Iの問題では、160.0から5.0の階級幅で度数分布表を作ってください。表IIの問題では、表IIの2の区分に従って度数分布表を作ってください。)
データの取り込み方:キーボードから入力しなくても、画面上で下向きにドラッグ・コピーし、Excel上に単純に貼り付けるとExcelデータになります。(単純なテキストデータなので、安全に取り込むことができます。)
表I 表II 表IIの2
|
≪解答例≫ 表Iの問題
表IIの問題
■読み終わったら→ ここ ←をクリック■ |