|
■連立方程式
同次(斉次)連立一次方程式
A=…(1) が自明でない解 ≠ をもつための必要条件は det(A)=0
もし,det(A)≠0ならば,逆行列A−1が存在することとなり,(1)に左からA−1を掛けると,
detA−1A=A−1 したがって = となる.すなわち自明解のみをもつ. この対偶をとれば上記の結果を得る 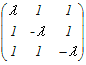 =0を解くと =0を解くとλ det  − −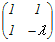 + +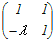 =0 =0λ(λ2−1)−(−λ−1)+(1+λ)=0 λ3+λ+2=0 (λ+1)(λ2−λ+2)=0 λ2−λ+2=0の解は虚数であるから 実数解はλ=−1
正確には,λ=−1のときに,実際に自明でない解をもつことを示さなければならないが,選択問題の解はただ一つであり,これ以外には解はないから,確かめるまでもない
→ 1 |
○この頁に登場する【問題】は,公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です.(=公表された著作物の引用)
○【解説】は個人の試案ですが,Web教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます. 問題や解説についての質問等は,原著作者を煩わせることなく,当Web教材の作成者(<浅尾>)に対して行ってください. 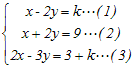 の(1)(2)がただ一つの解をもつから(図形的には1点で交わるから),(1)(2)(3)が解をもつためには,(1)(2)の解が(3)を満たせばよい(図形的には(3)が(1)(2)の交点を通ればよい) (1)(2)を解くと x=, y= これが(3)を満たせばよいから (k+9)−3()=3+k より 4x+36−27k+3k=12+4k 3k=3 k=1 → 1 |
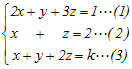 (2)+(3)より 2x+y+3z=2+k…(4) (4)は(1)と平行(な平面)だから,解が存在するためには,これらが一致しなければならない 2+k=1 k=−1 → 2 ≪別解≫ (2)(3)をx, yの方程式として解くと(zで表すと)  x=(2−z), y=(k−2z)−(2−z)=k−z−2 この解が(1)を満たせばいよいから 2(2−z)+(k−z−2)+3z=1 k=−1 |
方程式ax=bの解は
(ア) a≠0のときは,ただ1つx=に定まる. (イ) a=0, b=0のときは,不定(無数に多くの解) (ウ) a=0, b≠0のときは,不能(解は存在しない) ※(ア)において,b=0とb≠0に分ける必要はない.b=0のときは,上記の結果に単純にb=0を代入すれば,x=0が得られる 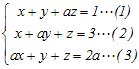 xを消去すると (2)−(1) (a−1)y+(1−a)z=2…(4) (3)−(1)×a (1−a)y+(1−a2)z=a…(5) (4)+(5)によりyを消去すると (−a2−a+2)z=a+2 (a2+a−2)z=−(a+2) (a+2)(a−1)z=−(a+2)…(6) (6)より (ア) a≠−2, 1のときは,解はただ1つに定まる(zがただ1つに定まると,x,yもただ1つに定まる)⇒題意に適さない (イ) a=−2のときは,無数に多くの解がある(zが不定になると,x,yも不定になる)⇒題意に適する (ウ) a=1のときは,解はない(zが存在しなければ,方程式の解はない)⇒題意に適さない → 1 |
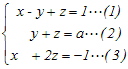 (3)−(1) y+z=−2…(4) (2)と(4)は(3次元空間の)平行な平面になるから (ア) a≠−2のときは解はない. (イ) a=−2のときは一致し,解は無数にある. (その平面上の点(x,y,z)はすべて解となる) 以上により,解をもつのは(イ)の場合 → 1 |
方程式ax=bの解は
(ア) a≠0のときは,ただ1つx=に定まる. (イ) a=0, b=0のときは,不定(無数に多くの解) (ウ) a=0, b≠0のときは,不能(解は存在しない) 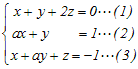 (1)−(3)×2によりzを消去する −x+(1−2a)y=2…(4) (2)+(4)×aによりxを消去する {1+a(1−2a)}y=1+2a (−2a2+a+1)y=(2a+1) (2a2−a−1)y=−(2a+1) (2a+1)(a−1)y=−(2a+1) a=−のとき,yは不定→(x,y,z)は無数に存在する → 1 |
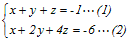 (2)−(1) y=(−3z−5)…(3) (3)を(1)に代入 x=(−z−1)−(−3z−5)=(2z+4)…(4) (3)(4)より,z=tとおいてtによる媒介変数で表すと x=(2t+4), y=(−3t−5), z=(t) ==z 各辺に2を足すと ==z+2…(*) → 1  ≪参考≫
≪参考≫2平面(1)(2)の共有部分が直線(*)の方程式になります. 点A(x0, y0, z0)を通り,方向ベクトル=(a, b, c)に平行な直線の方程式は == で表されますが,この点A(x0, y0, z0)の選び方は自由で,直線上にある他の点B(x1, y1, z1)でもよい.この点の選び方が上記の答案で「各辺に2を足す」という操作に対応しています. |
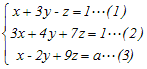 (2)−(1)×2 x−2y+9z=−1…(4) (4)は(3)と平行な平面だから,a=−1のとき(一致するとき)に限り,解がある. → 2 |
 が
が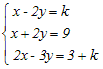 が解をもつとき,定数
が解をもつとき,定数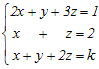 が解をもつとき,定数
が解をもつとき,定数 の解が無数に存在するとき,
の解が無数に存在するとき, が解をもつとき,定数
が解をもつとき,定数 の解が無数に存在するとき,定数
の解が無数に存在するとき,定数 と同値な直線の方程式は,次のどれか.
と同値な直線の方程式は,次のどれか. が解をもつとき,
が解をもつとき,