|
高校〜大学基礎の数学用語.公式.例
1.連続
continuous(1変数の関数 用語
関数
(詳しく言えば)となるとき,この関数
極限値
(さらに詳しく言えば)関数値 かつ,それらが等しいとき…(3) この関数
極限の存在については,次のように分けて調べなければならない場合がある
左側極限
右側極限 かつ,それらが等しいとき…(1.3) 極限が存在するという (まとめ) 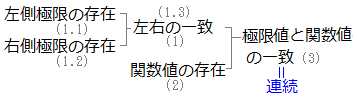 |
|
高校〜大学基礎の数学用語.公式.例
1.連続
continuous(1変数の関数 用語
関数
(詳しく言えば)となるとき,この関数
極限値
(さらに詳しく言えば)関数値 かつ,それらが等しいとき…(3) この関数
極限の存在については,次のように分けて調べなければならない場合がある
左側極限
右側極限 かつ,それらが等しいとき…(1.3) 極限が存在するという (まとめ)  |
2.連続とは,グラフが「つながっている」ということ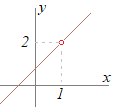 - 図1 - のグラフで, 他方で, だから,極限値は存在する(左右とも) 前述の(1.3)までは成立するが(2)が成立しないので,図1のように穴が開いたようなグラフになり, もし,関数が のように定義されていたら,この関数は 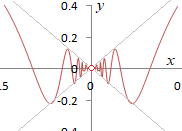 - 図2 - のグラフで, 他方で, だから,極限値は存在する(左右とも) 前述の(1.3)までは成立するが(2)が成立しないので,図2のように穴が開いたようなグラフになり, もし,関数が のように定義されていたら,この関数は |
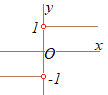 - 図3 - のグラフで, 他方で, だから,左右の極限は存在するが一致しない.したがって,(1)(2)とも成立せず この関数は,左右の極限が一致しないから,関数値 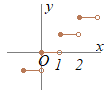 - 図4 - 右図4は, のグラフで, ア)
例えば,
イ)
例えば,
ア)イ)より,左右の極限が一致しないから,極限なし. *) 関数値は, 以上から,(1)の左右の極限の一致を満たさないから,不連続 |
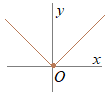 - 図5 - のグラフで, であるから 以上により,極限値,関数値が存在し,それらが一致するから, |
|
2変数関数の連続
【2変数関数における連続の定義】
2変数 (1) 関数値 (2) 極限値 (3) (1)(2)が等しいこと
ただし,(2)において
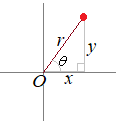 直交座標を極座標に直すには,次の関係式を用いる.
直交座標を極座標に直すには,次の関係式を用いる.この極座標を用いると,θの値に関わらず,r→0のとき一定の値に近づくならば,「(x, y)→(0, 0)のとき,どんな近づき方をしても一つの値に近づく」と言える. |
|
【例2.1】
(解答)次の関数の点 極座標を用いて, となり,近づき方(偏角 したがって, |
|
【例2.2】
次の関数の点
連続であるためには,(1)極限値が存在し,(2)関数値が存在し,(3)それらが等しくなければなりません.
(1)極限値が存在しないときや,(2)関数値が存在しないときは,直ちに不連続と言えます. 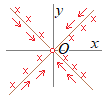 この問題のように,分母=0となる曲線(直線)が目指すべき点を通っている場合,近づき方によっては極限値が存在しないことになり,直ちに不連続と言えます.
この問題のように,分母=0となる曲線(直線)が目指すべき点を通っている場合,近づき方によっては極限値が存在しないことになり,直ちに不連続と言えます.
極限値が存在しないから,不連続…(答) (別解) 極座標を用いて, は近づき方(偏角 [ |
|
【例2.3】
(解答)次の関数の点 直交座標での点(1, 2)を極とし,x軸の正の向きを始線とする極座標を導入する とおく. よって,極限なし.不連続…(答) |
|
【例2.4】
(解答)次の関数が点 極座標を用いて, したがって, |
|
【例2.5】
(解答)次の関数が点 極座標を用いて, したがって, |