区間，単調関数

高校～大学基礎の数学用語.公式.例

　実数 $R$ の部分集合を区間という．
　端点(たんてん) $a,\hspace{2}b$ を含まない区間 $\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}a\lt x\lt b\}$ を開区間といい， $(a,\hspace{2}b)$ で表す．
　端点 $a,\hspace{2}b$ を含む区間 $\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}a\underline{\le}x\underline{\le}b\}$ を閉区間といい， $[a,\hspace{2}b]$ で表す．
　片方の端点のみ含む区間 $\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}a\underline{\le}x\lt b\}$ や $\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}a\lt x\underline{\le}b\}$ は半開区間と呼ばれ，各々 $[a,\hspace{2}b),\hspace{3}(a,\hspace{2}b]$ で表される．

話題

　無限大 $\infty$ や負の無限大 $-\infty$ は特定の数ではないが，これらを端点とする区間を表すときは，必ず開区間（半開区間）で表す．
$\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}-\infty\lt x\lt\infty\}$ もしくは $(-\infty,\hspace{2}\infty)$
$\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}a\underline{\le} x\lt\infty\}$ もしくは $[a,\hspace{2}\infty)$
$\{\hspace{2}x\mid\hspace{2}x\in R,\hspace{2}-\infty\lt x\underline{\le} b\}$ もしくは $(-\infty,\hspace{2}b]$

例

• 無理関数 $\sqrt{x}$ は，半開区間 $[0,\hspace{2}\infty)$ で連続である．
• 対数関数 $\log_e{x}$ は，開区間 $(0,\hspace{2}\infty)$ で連続である．
• 三角関数 $\sin x,\hspace{3}\cos x$ ，指数関数 $e^x$ は，開区間 $(-\infty,\hspace{2}\infty)$ で連続である．

話題

　関数の連続性は，区間の端点も含めて考えることができるが，微分可能性は区間の端点では考えられない．そこで，平均値の定理など，連続性と微分可能性について述べる場合，「閉区間 $[a,\hspace{2}b]$ で連続で，開区間 $([a,\hspace{2}b)$ で微分可能であるとき，...」のように書かれることが多い．

　区間Iで定義された関数 $f(x)$ が
$x_1\lt x_2$ ならば $f(x_1)\lt f(x_2)$
を満たすとき， $f(x)$ は区間Iで単調増加であるといい， $f(x)$ を単調増加関数という．
　区間Iで定義された関数 $f(x)$ が
$x_1\lt x_2$ ならば $f(x_1)\gt f(x_2)$
> を満たすとき， $f(x)$ は区間Iで単調減少であるといい， $f(x)$ を単調減少関数という．
　単調増加関数と単調減少関数を総称して単調関数という．

【例】
• $f(x)=x^2$ は $0\underline{\le}x\lt\infty$ において単調増加であり， $-\infty\lt x\underline{\le}0$ において単調減少である．

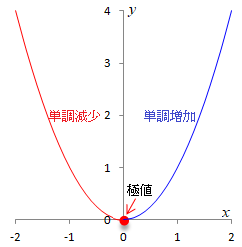
　導関数の符号によって関数の増減を調べると， $f\apos(x)=2x$ だから， $x\gt 0$ のとき $f\apos(x)=2x\gt 0$ となり， $x\lt 0$ のとき $f\apos(x)=2x\lt 0$ となる．高校で微分の基本を学んだ人にとって，開区間 $0\lt x\lt\infty$ において単調増加であり，開区間 $-\infty\lt x\lt 0$ において単調減少であることについては，異論がないでしょう．
　しかし，初めの式をよく見ると， $x=0$ は単調増加の区間にも，単調減少の区間にも入っているのであるから，「獣軍団と鳥軍団の両方に付いているコウモリ」のようになっており，「極値はどっちの味方なんだ！」と関心を持つのも悪くない．
　一般に次のようにまとめることができる．

閉区間 $[a,\hspace{2}b]$ で連続，開区間 $(a,\hspace{2}b)$ において微分可能な関数が，開区間 $(a,\hspace{2}b)$ においてつねに $f\apos(x)\gt 0$ ならば閉区間 $a\underline{\le}x\underline{\le}b$ において単調増加（減少）であるといえる…通俗的に言えば，単調増加，単調減少は端点を「飲み込む」（=数学用語ではない）ことができる．

　このようにして，一般に極値となっている点は，（コウモリのように）単調増加の区間にも，単調減少の区間にも入る．

話題

**（続き）**
【例】
　次の図は $y=\sin x$ のグラフで，極値は増加の区間にも減少の区間にも入る．

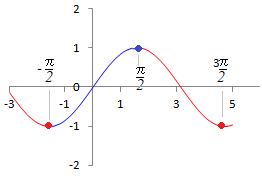
$-\frac{\pi}{2}\underline{\le}x\underline{\le}\frac{\pi}{2}$ において単調増加
$\frac{\pi}{2}\underline{\le}x\underline{\le}\frac{3\pi}{2}$ において単調減少
※ただし，高校では，次の表のように増減表と極値を作成することが多いので，「 $a\underline{\le}x\underline{\le}b$ において単調増加（減少）」のように文章で書く場合だけではない．

$x$	…	$-\frac{\pi}{2}$	…	$\frac{\pi}{2}$	…
$f\apos(x)$	$\hspace{1}-$	$0$	$+$	$0$	$\hspace{1}-$
$f(x)$	$\searrow$	極小	$\nearrow$	極大	$\searrow$

話題

**（つながってしまう場合）**

【例】
　次の図は $y=x^3$ のグラフで， $y\apos=3x^2$ だから， $-\infty\lt x\lt 0$ のとき $y\apos\gt 0$ ， $0\lt x\lt\infty$ のとき $y\apos\gt 0$ となる．
　したがって， $-\infty\lt x\underline{\le}0$ のとき単調増加， $0\underline{\le}x\lt\infty$ のとき単調増加となり，結局
$-\infty\lt x\lt \infty$ のとき単調増加
と言える．