← PC�p�͕ʕ�
|
�Ⴑ�̃y�[�W���̖ڎ��� |
|
1.3�@����
�@��
�@�� �@ �@ �@�� |
|
1.4�@���K����
�@����
�Ȃǂ̋L���ŕ\�����D �@��ʂɁC�� �Ȃǂ̋L���ŕ\�����D �@��2���ȏ�̓��������������i���K�����j�Ƃ����D
�y��1.4.1�z�@���̊��̑�n�������in�K�����j�����߂Ă��������D�i�������Cn�͐��̐����Ƃ���j
�i�j���
�A�j
�C�j �E�j
�y��1.4.2�z�@���̊��̑�n�������in�K�����j�����߂Ă��������D�i�������Cn�͐��̐����Ƃ���j
�i�j(1) (2) (1) (2)
�y��1.4.3�z�@���̊��̑�n�������in�K�����j�����߂Ă��������D�i�������Cn�͐��̐����Ƃ���j
�i�j(1) (2) (1) (2)
��d�K��̋L��
�A�j �C�j �����̖��ł́C��̓�d�K�悾�����o�ꂷ��
�y��1.4.4�z�@���̊��̑�n�������in�K�����j�����߂Ă��������D�i�������Cn�͐��̐����Ƃ���j
�i�j(1) (2)  (1)
(1)
�����́C���̂悤�ɂ܂Ƃ߂邱�Ƃ��ł��� 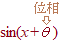 ���Ȃ킿�C�������͈ʑ���
���Ȃ킿�C�������͈ʑ���
 (2)
(2)
�����́C���̂悤�ɂ܂Ƃ߂邱�Ƃ��ł���
���Ȃ킿�C�]�����͈ʑ���
�������E�]�����͈ʑ��� �����ڊ�
�y��1.4.5�z�@���̊��̑�n�������in�K�����j�����߂Ă��������D�i�������Cn�͐��̐����Ƃ���j
�i�j(1) (2) (1) (2)
�y��1.4.6�z
�i����j��C�v�j�b�c�̌�����`�ς̔����@�ɂ��ā` �ȉ���n�ɂ��Ă̐��w�I�A�[�@�ɂ���ďؖ��ł���D �i�T�j n=1�̂Ƃ� ���Ȃ킿 �͐ς̔����@�ɂ�萬������D �i�U�j n=m�̂Ƃ� �����藧�Ɖ��肷���
�@�ȉ��̕ό`�́C�O���猩�Ă���Ƌ@�B�I�������͖��������Ɍ����邩������Ȃ����C�V�O�}�L���̓Y�����̕t�������C�����ԖڂƊ�ԖڂŏW�ߒ����āC���ލ��̌W�������Ă��邾���ł���D��̓I�Ɋe���������o���Ă݂�ƕό`�̈Ӗ���������D
(�T)(�U)���Cn=m+1�̂Ƃ������藧����C���w�I�A�[�@�ɂ�肷�ׂĂ̎��R��n�ɂ��Đ��藧�¥�����ؖ��I��������  �F���̌` �F���̌`�����ŁC���F�ŏ����ꂽ���ɂ��āC���̑g���������i���Z���wA�ŏK���j���g���D ���̖��ł� ���������āC�����̕����� �S�̂� �����ʂȂ����m�ł����Ă��C �����ʂ��悭�C�ԈႢ�����Ȃ��u���܂��b�v�Ɋ���悤�D �����̗��^���āC���C�v�j�b�c�̌�����g�ݍ��킹�āC���ʂ��悭�ό`����Ƃ悢�D |
|
�y��1.4.6.1�z
�i�j�����ŁC �@�i�`���I�ȋL�� �ł��邩��i ����ɁC �ł��邩�� ����ɉ����āC �ł��邩��
�y��1.4.6.2�z
�i�j�����ŁC �ł��邩��i ↑�y��1.4.3�z���g���� ���`�������ނ悤�ȕό`�Ɋׂ��Ă����`�u�c�u�c �Ȃ��C |
|
�y��1.4.6.3�z
�i�j
���̖���(A)
(A)���C�v�j�b�c�̌����́u���܂��b�v�ł����C�������������̂悤�Ɂu�萔�{�̘a���ɕ�����ό`�v�́C�u�����Ƃ��܂��b�v�ł��D �̂悤�ɂQ�̊��̐ςƌ��Ȃ��ƁC���C�v�j�b�c�̌����ɂ��
������
������
�V�O�}�L���́C������ (B) |
|
�y��1.4.6.4�z
�i�j
���̖����O��Ɠ��l��(A)
�i�j(B)�̏��Ɨ]��ɕ�������@�̂ݎ�����
������
�y��1.4.6.5�z
�i�j
���̖����O��Ɠ��l��(A)���̐ςƌ��ă��C�v�j�b�c�̌�����K�p������@��(B)�O�p���̐ς�a�ɒ������@�̂Q���l�����܂����C(B)�̕����y�ɂł��܂��D
�i�j���ς́C�u���`���D���v�u�萔�{�Ƙa���ɕ�����ƗL���v�ƌ����܂� (B)�̕��@ �O�p���̐ς�a�ɒ��������ɂ�� ���ɁC�O�p���̔������� �ɂ�� ������ (A)�̕��@ ������ ���g���� �O�p���̐ς�a�ɒ��������ɂ��  �E�}�̂悤��
�E�}�̂悤�������藧����
�藝�ɂ��
|
|
1.5�@�A�������\�CCn���CC����
�@n�K�������A���ł���悤�Ȋ�
[1]�@�܂��C�u
�@1.2�́u�A���Ɣ����\�v�̍��Ŏ������悤�ɁC�����\�Ȃ�ΘA���ł���̂ŁC�������ɂ��Ĕ����\�̏�ɂ���ɘA���������K�v�͂Ȃ��D
�@���̂悤�Ɍ��������Ă��悢�D�u �u [2]�@���ɁC�������铮��́un���������v�����̎����[�āC�ł������́un�K�����v���K�̎����[�Ă�D �@���Ȃ킿�C �@�v��C�uCn�����Ȃ킿 �@���������āC���鐳�̐���n�ɂ��āCCn���ƌ�����ꍇ�́CC1���`Cn−1���܂ł̂��ׂĂɊY������D �@Cn���Ƃ����p�ꂪ���̂悤�ɒ�`����Ă���ƁC���ۂɎg���Ƃ��ɕ֗��ɂȂ�D�Ⴆ�u�� [5]�@����ł��A�������\�ł�����́CC�����ƌĂ��D �@���Z���w�ɓo�ꂷ��Cn�����C�������C�������i�L�����j�̕��ꂪ�O�ɂȂ�Ƃ���ȊO�C�O�p���C�w�����C�ΐ����̐^�������̂Ƃ���ȂǁC����܂łɂ悭�o�ꂵ�Ă�������C�����ł���D���������āC�����̊��́CC1���CC2���CC3���C����̂�����ɂ��Y������D �@�܂��C�p����L���āC�� [6]�@�u���傤��n��A�������\�ŁCn+1��ȏ�͘A�������\�ł͂Ȃ��v������邱�Ƃ́C�ނ������D �@�O�q���y��1.1.2�z�̊� �@���ɁC�����1���ϕ��������i�������ȒP�ɂ��邽�߂ɒ萔�{����j �A�j�@ �C�j�@ �A�j�ƃC�j����v���邩��C �@�������C �@���l�ɂ��āC �@���̊��́C���C�G���V���g���X��1872�ɔ��\�������̂ŁC�u����Ƃ���A���ŁC����Ƃ�������s�\�Ȋ��v�̗�ƂȂ��Ă���D�i���\��������C�����Ō}����ꂽ���̂炵���j �i ���M�҂̔\�͂ł́C������₷����������͖̂����ł��邪�C��G�c�ȃC���[�W�Ƃ��ẮC�u�ǂ��܂ōׂ������čs���Ă��C�܂�Ȃ����Ă���u���E���^���̋O�Ձv�̂悤�Ȃ��̂��l����Ƃ悢�D �@��ʂɁu�A���ł����āC���C�����s�\�Ȋ���ϕ�����C1�������\�Ȋ��ɂȂ�C2��ϕ�����P�������\�Ȋ��ƂȂ�D�v �@����ɂ��C |
|
1.6�@�ߎ���
�y���ϒl�̒藝�z
�@�� ����  �@�ؖ��́C���Z���w�V���w�̋��ȏ��ɏo�Ă��܂��D�����ł́C�u�}���ɂ�芴�o�I�Ɂv�Ӗ������ނ��Ƃɂ��܂��D
�@�ؖ��́C���Z���w�V���w�̋��ȏ��ɏo�Ă��܂��D�����ł́C�u�}���ɂ�芴�o�I�Ɂv�Ӗ������ނ��Ƃɂ��܂��D�́C��� �A�j �C�j�@�t�ɁC �@���ǁCA����B�ɍs���Ȑ�
�@���ϒl�̒藝�̏d�v�ȓ_�̂P�́C��
�@���ϒl�̒藝�̕�����ƁC���Ȃ킿 |
|
�y�P���̋ߎ����z
���ϒl�̒藝�̕�������� �ɂ����āC�����W���i�X���j�Ƃ��� �Ƃ�������������D���̎��́C�^�̒l 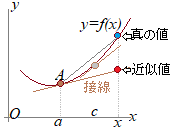
�y��1.6.1�z
�i�j
�y��1.6.2�z
�i�j
�y��1.6.3�z
�i�j���ɁC46�����ʓx�@�ɒ���
�y��1.6.4�z
�i�j
�y��1.6.5�z
�i�j |
|
�y�Q���̋ߎ����z
�i����j�@�� �ŕ\�����D �@�� �ƂȂ�悤�ɒ萔 �@���ӂ� �@�� ���� �����ŁC���� (*1)(*2)���� �ȏ�ɂ��C���������D ���ʏ�C2���̋ߎ����܂ł��������C���l�ɂ��āC3���C4���̋ߎ��������߂�Ǝ��̌`�ɂȂ�D �i�Q�l�j �@�u �̂悤�ɁC �@����ɑ��āC�ʏ�悭���鎟�̌`�́C�u |
|
�y��1.6.6�z
�i�j
�y��1.6.7�z
�i�j |
|
1.7�@�덷�̌��E
�@��L�́y��1.6.2�z�`�y��1.6.6�z�Ȃǂɂ����āC������4�ʂ܂ł̋ߎ��l�����߂��肪���������C�����̖��ɂ����āu�^�̒l�Ə�����4�ʂ܂ł̋ߎ��l����v����v�Ƃ������Ƃł͂Ȃ��D���ʂȈӖ������������ɁC�ߎ������g���ď����扽�ʂ܂ŋ��߂Ă݂悤�ƌ����`�ŋߎ����̎g��������K���������ł���D�@����ɑ��āC�^�̒l�Ƌߎ��l�Ƃ́u�덷�̌��E�v�ׂ����Ƃ��́C���̂悤�ɋ��߂�D �P���̋ߎ����� �Q�K�����܂ŗp���Đ^�̒l�����߂�� �i�������C
(1)��(2)�̍����덷�ł��邩��C�덷���R�K�����܂ŗp���Đ^�̒l�����߂�� �i�������C
(3)��(4)�̍����덷�ł��邩��C�덷�����C��]���Ƃ����D���ۏ�́C �@�y��1.6.2�z�ł́C �@���̋ߎ��l�̌덷�̌��E�́C���̂悤�ɂ��Čv�Z�ł���D ������ �덷�̌��E�� �@���������āC������Q�ʂ���덷�������ė���\��������D �@�y��1.6.5�z�ł́C �@�Ⴆ�Cx=0.1�̂Ƃ��̋ߎ��l�́C1.1�ɂȂ�C���̌덷�̌��E�͎��̂悤�Ɍv�Z�ł���D ������Cx=0.1�̂Ƃ��C�덷�̌��E�� �@���������āC������3�ʂ���덷�������ė���\��������D �@���̓������łQ���̋ߎ����܂ŋ��߂�ꍇ�C�ߎ����� ������Cx=0.1�̂Ƃ��C�덷�̌��E�� �@���������āC������4�ʂ���덷�������ė���\��������D |
|
�y��1.7.1�z
�i�j�@ �Ƃ����� x=0�̂܂��̂P���̋ߎ����� |
|
1.8�@�e�C���[�̒藝
�y�e�C���[�̒藝�z�i�L���e�C���[�W�J�j
�i����j�@�� �@������ ����]���ƌĂ��D �@��]���́C �y�}�N���[�����̒藝�z�i�L���}�N���[�����W�J�j �@�e�C���[�̒藝�ɂ����āC���� �@������ ����]���ƌĂ��D �@��]���́C �@�Q���̋ߎ����C�܂ł͊��ɏq�ׂĂ���̂ŁC�����ł͂R���̋ߎ����ׂĂ݂�D �ƂȂ�萔 �@���ӂ� �@����ɁC���ӂ� �@�� �ƂȂ� �@���l�ɂ��āC(n−1)���̋ߎ��������߂�ƁC�e�C���[�̒藝��������D���ɁC |
|
�y�e�C���[�����z�i�e�C���[�W�J�j
�@�� �ƂȂ�ꍇ�C ���Ȃ킿 �i�������C �ׂ̂������� �y�}�N���[���������z�i�}�N���[�����W�J�j ���Ȃ킿 �ׂ̂��������}�N���[���������Ƃ����D�܂��C���̌`�ɕ\�����Ƃ��}�N���[�����W�J�����Ƃ����D |
|
�y��1.8.1�z
�i�j�@
(1)
���e�X���߂Ă��������D�i�����̎��������ɂ��ẮC��œo�ꂷ��̂ŁC�����ł͎����������������Ȃ��Ă��悢�j
(2) (3)n���܂ł̗L���}�N���[�����W�J (4)�}�N���[�������� (1) �i�������C (2) (3) �i�������C (4) |
|
�y��1.8.2�z
�i�j�@���̊��̃}�N���[�����W�J�����߂Ă��������D (1) (2) (3) (4) (1) �Ƃ����� (2) �Ƃ����ƁC�y��1.4.4�z(1)�̌��ʂ��� (3) �Ƃ����ƁC�y��1.4.4�z(2)�̌��ʂ��� (4) �Ƃ����ƁC�y��1.4.3�z(1)�̌��ʂ��� ������C |
|
�i���̑��C����̊��̃}�N���[�����W�J�m���ʂ̂݁n�j ���O�p�� (#1) �i�x���k�[�C���� �ɂȂ��Ă���j (#2) �i�x���k�[�C���� �ɂȂ��Ă���j ���t�O�p�� (#3) �i���̋����̈�ʍ�(n��1)�� �ɂȂ��Ă���j (#4) (#5) ���o�Ȑ��� (#6) (#7) (#7) |
|
�y��1.8.3�z
�i�j�@���̊��̃}�N���[�����W�J��
�ς̔����@�⏤�̔����@���g�������C���Ɨ]��ɕ����āu�������͕x�m�̎R�v�i�����̗p��j�Ƃ�������ȒP�ɂȂ邱�Ƃ�����
�̂悤�ɕό`���Ă��獂�K���������߂�Ƃ悢�D �Ƃ���
�y��1.8.4�z
�i�j�@���̊��̃}�N���[�����W�J��
�@�S�������Ȃ������獂�K�������v�Z���Ă��������C���m�̌��ʂ��g�����ʂł́C���܂����p����������ʂ��悭�C�v�Z�ԈႢ�����Ȃ��Ȃ�܂��D
����C������ς���� ����ɁC���ӂ� �i�@�j�ȍ~�͕s�v |
|
�y��1.8.5�z
�i�j�@���̊��̃}�N���[�����W�J��
�@�S�������Ȃ������獂�K�������v�Z���Ă��������C���m�̌��ʂ��g�����ʂł́C���܂����p����������ʂ��悭�C�v�Z�ԈႢ�����Ȃ��Ȃ�܂��D
�y��1.4.5�z(1)�̂悤�ɎO�p���̍����ɂ����@�C���̐ςɑ��ă��C�v�j�b�c�̌������g�����@������܂��D���̑��C�S���̍��܂łƂ����w��𗘗p����ƁC���̕��@���g���܂��D �T���ȏ�̍��͊|����K�v���Ȃ� |
|
1.9�@�������a
�@�e�C���[������}�N���[���������͖��������ƂȂ�̂ŁC�������a���l����K�v������܂��D�@�ڂ����́C���̃y�[�W�C���̃y�[�W�Q��
�@�قƂ�ǂ̋����̎�������́C�_�����x�[���̔���@�łł���D����Ń_���ȂƂ��̓R�[�V�[�̔���@������D
�y�_�����x�[���̔���@�̗v�_�z�@������������ �ƂȂ�萔 �ƂȂ�Ƃ��C �@���������āC�������� �ƂȂ�萔 �@�ׂ������i�������j ���C�������邽�߂̏����� �ł��邩��C�ׂ��������������邽�߂� ���Ȃ킿�C�������a ���قƂ�ǂׂ̂������́C�B�̌`�� �@�������̍��C����̍��������琬��ׂ������Ȃǔ��f������Ƃ��́C�@�A�ɖ߂��Ĕ��f���Ă��悢�D ���قƂ�ǂׂ̂������ɂ��āC�������a�̓_�����x�[���̔���@���g�����߂���D�i�R�[�V�[�̔���@���K�v�Ȃ��̂͏��Ȃ��j
�y��1.9.1�z
�i�j�@���̊����}�N���[�����W�J���C���̎������a�����߂Ă��������D �@�}�N���[�����W�J�̋��ߕ����y��1.8.1�z�Q�� �@�������a��
�y��1.9.2�z
�i�j�@���̊����}�N���[�����W�J���C���̎������a�����߂Ă��������D �@�}�N���[�����W�J�̋��ߕ����y��1.8.2�z(2)�Q�� �@�`���I�Ɏ������a�����߂悤�Ƃ���ƁC���̖��̂悤�Ɋ��̍��������琬�藧���Ă���ꍇ�� �̌v�Z�ɂ����āC����╪�q��0�ɂȂ��ē��f���Ă��܂���������Ȃ��D���̂悤�ȏꍇ�́C�@�A�ɖ߂��Č�������悢�D �̂Ƃ���������D���Ȃ킿 �@�������a�� |
|
�y��1.9.3�z
�i�j�@���̊����}�N���[�����W�J���C���̎������a�����߂Ă��������D �@�}�N���[�����W�J�̋��ߕ����y��1.8.2�z(4)�Q�� �������a��
�y��1.9.4�z
�i�j�@���ׂ̂������̎������a�����߂Ă��������D ��� |
|
�y��1.9.5�z
�i�j�@���ׂ̂������̎������a�����߂Ă��������D
�y��1.9.6�z
�i�j�@���ׂ̂������̎������a�����߂Ă��������D �������`�h���g���Ċw�K����Ƃ��̎Q�l �����`�hGoogle Gemini�CMicrosoft Copilot�CChatGPT�Ȃǂ��g���Ƃ��C (1) ���̂[�W�ɂ���ǂ̖��ł��A��肪�^����ꂽ��Ɠr���o�߂͏�����D (2) �������A�ǎ҂̃��x���ɉ����������o�����Ƃ́A�Ȃ��Ȃ�����悤�ł���D�T���āA�����`�h�́u�ǎ҂���w���x�̒m����������̂Ƃ��āC�g����m����S���g���ĉ����X��������v�D���̂��߁A���{�̏������̐��k�����̗��K�����o���Ă��炨���Ƃ���ƁA�N��ɂ���Ċw�K�w���v�̂Œ�߂�ꂽ�w�K�͈͂��ς�邱�Ƃ́A�قږ��������D�����ŁC���w���Z�������̖��ł��C�u����̉��������g�킸�Ɂv�ȂǂƉ������ɐ����������Ȃ��ƁC�����铚�Ă��Ԃ���Ȃ����Ƃ�����B �@�܂��C���̎����ڂ����w�肵�Ȃ���C�₳���߂�������肪���Ԃ��Ƃ�����D�Ⴆ�C�u�����̎������a�����߂���K�����T����A���̉������Ɖ������Ă��������B�v�Ɠ��͂����ꍇ�C�������̖����肪���Ԃ��Ƃ�����D���������ꍇ�C�u�����C�������C�w�����C�O�p���C�ΐ������炻�ꂼ��P�₸���v�T����C����v�ȂǂƖ��̎����ڂ����w�肵�Ȃ���C���҂������̎��ƈقȂ�ꍇ������D |
|
|