【この頁の要約】
　この頁で解説する内容は，ほぼ次のようにまとめることができます．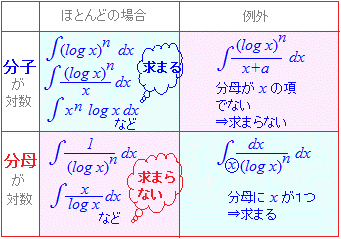
【logxに関する不定積分≪一覧≫】
○［(log x) n dx (n≠0)］
.logx dx=xlogx−x+C…(*5.1)
.(logx)2dx=x(logx)2−2xlogx+2x+C…(*5.2)
.In=(logx)ndx (n=0,1,2,..)とおくと
.In=x(logx)n−n In−1 (n=1,2,3,..)…(*5.3)
○［xnlogx dx ,dx (n≠1)］
.xnlogx dx=xn+1(logx−)+C…(*5.4)
○［dx (n≠−1)］
.dx=+C…(*5.5)
○［xm(logx)ndx (m≠−1)］
Im,n=xm(logx)ndx (m≠−1)とおくと，次の漸化式が成り立つ
Im,n=(logx)n−Im,n−1…(*5.6)
○［(n>0) , dx　(n≠−1)］など
　⇒　初等的には求められません．…(*5.7)
は初等的に表せず，これを表すために
Li(x)：対数積分（Logarithmic integral function）という特別な関数を定義する必要があります．
他のdxはLi(x)と漸化式の関係で
つながっていますが，「第１ボタンでつまづいている（初等的に表せない）」ので，分母にlogxがある関数の不定積分を初等的に求めようとすると，「全部つまづく（初等的に表せない）」ことになります．

　しかし，次のように分母にxが１つだけ付いているものは，例外的に求められます
.=−+C (n≠1)…(*5.8)
.=log|logx|+C…(*5.9)
○［log（２次式）dx］
.log(x2+a2)dx=xlog(x2+a2)−2x+2atan−1+C
(a>0)…(*5.10)
.log(x2−a2)dx
.=(x+a)log|x+a|+(x−a)log|x−a|−2x+C
(a>0)…(*5.11)
○［xlog(x2+a2)dx (a>0)］
.xlog(x2+a2)dx={(x2+a2)log(x2+a2)−x2}+C
(a>0)…(*5.12)
○［log(x+)dx (a>0)］
.log(x+)dx
.=xlog(x+)−+C
(a>0)…(*5.13)
（解説）
(*5.1)←
logx dxを1·logx dxに
分けて部分積分を行う．
f(x)=log xf’(x)=
g’(x)=1g(x)=x

1·logx dx=xlogx−x dx=xlogx−dx
=xlogx−x+C
この結果を微分すると，簡単に検算できます．
(xlogx−x)’=1·logx+x·−1=logx
(*5.2)←
(logx)2dx=(logx)(logx)dx
部分積分を行う．
f(x)=(logx)2f’(x)=2logx
g’(x)=1g(x)=x
1·(logx)2dx=x(logx)2−2logx dx
=x(logx)2−2xlogx+2x+C
※次のように行ってもできる．
f(x)=logxf’(x)=
g’(x)=logxg(x)=xlogx−x
(logx)(logx)dx=logx(xlogx−x)−(logx−1)dx
=x(logx)2−xlogx−(xlogx−x−x)+C
=x(logx)2−2xlogx+2x+C
(*5.3)←
In=(logx)ndx (n=0,1,2,..)とおくと
まず，I0=(logx)0dx=dx=x+Cとなる
n≧1のとき
In=1·(logx)ndx
f(x)=(logx)nf’(x)=n(logx)n−1
g’(x)=1g(x)=x
In=x(logx)n−n(logx)n−1 x dx
=x(logx)n−n(logx)n−1dx
=x(logx)n−n In−1
これを利用して，順次求めることができます．（漸化式から一般項を求めるのは無理）
I1=xlogx−x+C
I2=x(logx)2−2I1=x(logx)2−2(xlogx−x)+C
I3=x(logx)3−3I2=x(logx)3−3(x(logx)2−2xlogx+2x)+C
(*5.4)←
xnlogx dx=Iとおいて部分積分を行う
f(x)=logxf’(x)=
g’(x)=xng(x)=xn+1
I=xn+1logx−xndx
=xn+1logx−xn+1+C
=xn+1(logx−)+C
［ｎが正の整数である場合の例］
.x2logx dx=x3(logx−)+C
［ｎが負の整数（≠−1）である場合の例］
. dx=x−2logx dx
=x−1(logx−)+C
=−(logx+1)+C
※同様にして
.dx , dx (a≠0)

なども部分積分で求められるが
.dx (a≠0)は求められない
［ｎが分数である場合の例］
.logx dx=xlogx dx
=x(logx−)+C
=x(logx−)+C
≪参考≫
　与えられた関数の不定積分を求めたいとき，どんな関数でも不定積分が求められるという訳ではないことに注意しなければなりません．
　以下においては，多項式，分数関数，無理関数（累乗根），三角関数，指数関数，対数関数の「有限回の」和差積商や合成によって得られる関数を初等関数と呼ぶことにします．
　初等関数の微分は初等関数になりますが，初等関数の不定積分は必ずしも初等関数の範囲内にあるとは限りません．
　定期試験や入学試験などでは「解ける」問題だけが出題されていますが，各自で自由に思い浮かべた関数に対していつでもその不定積分を初等的に表現できるとは限らないことに注意してください．
(*5.5)←
log x=tとおいて置換積分を行うと
= → dx=x dtだから
dx=x dx =+C
=+C
［ｎが正の整数である場合の例］
.dx=+C
［ｎが分数である場合の例］
.dx=logx+C
(*5.6)←
Im,n=xm(logx)ndx (m≠−1)とおくと
f(x)=(logx)nf’(x)=n(logx)n−1
g’(x)=xmg(x)=xm+1
Im,n=xm+1(logx)n−xm+1n(logx)n−1dx
=xm+1(logx)n−xm(logx)n−1dx
=xm+1(logx)n−Im,n−1
［この公式の特別な場合として］
・［m=0, n=1のとき，(*5.1)になります］
I0,1=x0(logx)1dx=x1(logx)1−I0,0
ここで
I0,0=x0dx=x+Cだから
logx dx=xlogx−x+C…(*5.1)
・［m=0, n=1のとき，(*5.2)になります］
I0,2=x0(logx)2dx=x1(logx)2−I0,1
ここで
I0,1=x1dx=xlogx−x+Cだから
(logx)2dx=x(logx)2−2(xlogx−x)+C
・［m=0のとき，(*5.3)の漸化式になります］
I0,n=x0(logx)ndx=x1(logx)n−I0,n−1
⇒ In=x(logx)n−n In−1 (n=1,2,3,..)…(*5.3)
・［n=1のとき，(*5.4)になります］
Im,1=xmlogx dx=xm+1logx−Im,0
ここで
Im,0=xmdx=xm+1+Cだから
Im,1=xm+1logx−xm+1+C
=xm+1(logx−)+C
※以上のように(*5.6)は適用範囲の広い公式になっていますが，これを丸暗記して他のものは覚えないという学習方法は疑問です．むしろ，「部分積分」や「置換積分」をいろいろ「試してみればどれかでできる」という態度を身に付けるのがよいでしょう．
(*5.8)←

logx=tとおいて置換積分を行うと
= , dx=x dtとなるから
=x dt=t−ndt
=t−n+1+C=−+C…(*5.8)
※xが１つあるときだけ，ちょうど消えます
(*5.9)←

logx=tとおいて置換積分を行うと
= , dx=x dtとなるから
=x dt=dt=log|t|+C
=log|logx|+C…(*5.9)
※xが１つあるときだけ，ちょうど消えます
(*5.10)←
log(x2+a2)dx=Iとおく(a>0)
f(x)=log(x2+a2)f’(x)=
g’(x)=1g(x)=x
I=xlog(x2+a2)−x dx
=xlog(x2+a2)−2(1−)dx
=xlog(x2+a2)−2x+2a2dx
ここでJ=dxは次のように置換積分で求められます．
x=atant ←→ t=tan−1とおいて置換積分を行うと
= , ⇒dx==(1+tan2t)dtとなるから
J= a dt=t+C=tan−1+C
したがって
I=xlog(x2+a2)−2x+2atan−1+C
(*5.11)←
log(x2−a2)dx=log(x+a)(x−a)dx
={log(x+a)+log(x−a)}dx
ここで
logx dx=xlogx−x+Cだから
log(x2−a2)dx=(x+a)log|x+a|+(x−a)log|x−a|−2x+C
(*5.12)←
xlog(x2+a2)dx=I (a>0)とおく
x2+a2=tとおく置換積分により=2x , ⇒dx=となるから
I=xlogt =logt dt
=(tlogt−t)+C’={(x2+a2)log(x2+a2)−(x2+a2)}+C’
={(x2+a2)log(x2+a2)−x2}+C
(*5.13)←
log(x+)dx=I (a>0)とおく
f(x)=log(x+)=logp , p=x+とおくと
f’(x)=f(x)==(1+)
==となるから
次のように部分積分を行う
f(x)=log(x+)f’(x)=
g’(x)=1g(x)=x
I=xlog(x+)−dx
第２項をJ=dxとして求める
x2+a2=tとおくと=2x → dx=
J==dt=+C=+C’
I=xlog(x+)−+C
　以下の問題は，この頁のどこかに書かれている内容か，または，それを少しだけ変形したものです．正しい番号を選択してください．
［問題１］
次の不定積分を求めてください．
.log2x dx

1xlogx−x+C 2xlog2x−x+C
32xlogx−2x+C 42xlog2x−2x+C



［問題２］
次の不定積分を求めてください．
.(logx)2dx

1x(logx)2−2x+C
2x(logx)2−2xlogx+C
3x(logx)2−2xlogx+2x+C
4x(logx)2−2xlogx+x2−2x+C



［問題３］
次の不定積分を求めてください．
.dx
1−+log+C 2(logx−x)+C
3(logx−x)+C 4初等的には表せない



［問題４］
次の不定積分を求めてください．
.xlogx dx
1log(logx)+C
2+C
3x2(logx−)+C
4初等的には表せない



［問題５］
次の不定積分を求めてください．
.dx
1log(logx)+C
2+C
3x2(logx−)+C
4初等的には表せない



［問題６］
次の不定積分を求めてください．
.
1log(logx)+C
2+C
3x2(logx−)+C
4初等的には表せない



［問題７］
次の不定積分を求めてください．
.dx
1log(logx)+C
2+C
3x2(logx−)+C
4初等的には表せない



［問題８］
次の不定積分を求めてください．
.dx
1x+C
2x+C
3logx+C
4logx+C



［問題９］
次の不定積分を求めてください．
.log(x2+a2)dx(a>0)
1xlog(x2+a2)+2x−2atan−1+C
2xlog(x2+a2)−2x+2atan−1+C
3(x+a)log|x+a|+(x−a)log|x−a|−2x+C
4(x+a)log|x+a|−(x−a)log|x−a|−2x+C



［問題10］
次の不定積分を求めてください．
.log(x2−a2)dx(a>0)
1xlog(x2+a2)+2x−2atan−1+C
2xlog(x2+a2)−2x+2atan−1+C
3(x+a)log|x+a|+(x−a)log|x−a|−2x+C
4(x+a)log|x+a|−(x−a)log|x−a|−2x+C



..高卒〜大学数学のメニューに戻る　○===メニューに戻る
■［個別の頁からの質問に対する回答］[logxに関する不定積分について／18.9.21］
(*5.10)の解説の下の方にある、文言、したがって〜の、1行上の式の右辺の1/aは1/a^2ではないでしょうか？
＝＞［作者］：連絡ありがとう．その箇所のaの部分は，確かにおかしいですが，あなたの計算もおかしいです．訂正しました．