|
■全微分方程式→ 印刷用PDF版は別頁
■全微分とは
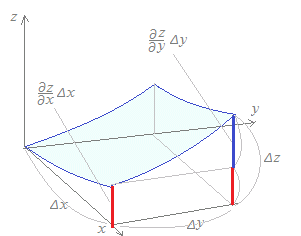
２変数の関数z=F(x, y)について，x, yの増分をΔx, Δyとするとき，zの増分Δzは Δz≒Δx+Δy で表されます． この式において，Δx→0, Δy→0となる極限を形式的に dz=dx+dy…(1) で表し，dzをzの全微分といいます．
はzのxに関する偏導関数で，yを定数と見なし
(1)式の形は，変数分離形の微分方程式を解く途中経過において，今までに何度も登場しています．て，xで微分したものを表し，x方向の傾きに対応します． 同様にして，はzのyに関する偏導関数で，xを 定数と見なして，yで微分したものを表し，y方向の傾きに対応します．
例えば
=−
y dy=−2 dx 2x dx+y dy=0 の変形において，『形式的に分母を払って』変形する場合においても，このような式が登場しています．
■全微分方程式，完全微分形とは
微分方程式が P(x,y)dx+Q(x,y)dy=0…(2) の形で与えられているとき，この微分方程式を全微分方程式といいます． (2)の形の全微分方程式で，P(x,y) , Q(x,y)が１つの関数 F(x,y)のx偏導関数とy偏導関数になっているとき，すなわち =P(x,y) , =Q(x,y) が成り立っているとき，この微分方程式は完全微分形と呼ばれます． 完全微分形の微分方程式の一般解は F(x,y)=C…(3) で与えられます． |
 z=x3y2のとき， =3x2y2 , =2x3y 【全微分の例】 z=x3y2のとき， dz=3x2y2dx+2x3ydy 【全微分がつねに０になる場合】 全微分がつねに０になる場合，すなわち dF=0 になる場合は，Fは定数になります．したがって，dF=0の解は F(x,y)=C （Cは任意定数） と言えます．
このように,全微分方程式が完全微分形になっていて，これを満たす関数F(x,y)が見つかる場合，全微分方程式の一般解は直ちに求まります． 例えば，全微分方程式 (3x2y2)dx+(2x3y)dy=0 については，F(x,y)=x3y2を想定すると，完全微分形であることが分かるので，この微分方程式の一般解は x3y2=C になります． ※ 通常の場合には，上記のような関数F(x,y)が簡単に見つかるとは限らないので (1) 完全微分形である場合に，F(x,y)を見つける方法は？
(2) 完全微分形になっていない全微分方程式を変形して完全微分形に直す方法は？
の２点がこの頁のテーマになります．
|
|
【例題１】
(1)変数分離形として解く：微分方程式=すなわちxdx−ydy=0を (1) 変数分離形として解いてください． (2) 全微分方程式として解いてください． y dy=x dx y dy=x dx =+C1 y2−x2=2C1=C…（答） (2)全微分方程式として解く： F(x,y)=−とおくと =x , =−y となるから F(x,y)=−について dx+dy=0 は完全微分形になる． −=C1 x2−y2=C…（答）
【例題２】
(1)変数分離形として解く：微分方程式exsiny dx+excosy dy=0を (1) 変数分離形として解いてください． (2) 全微分方程式として解いてください． =− dy=−dx dy=−dx log|siny|=−x+C1 |siny|=e−x+C1=eC1e−x siny=±eC1e−x=Ce−x exsiny=C…（答） (2)全微分方程式として解く： F(x,y)=exsinyとおくと =exsiny , =excosy となるから F(x,y)=exsinyについて dx+dy=0 は完全微分形になるから exsiny=C…（答） |
○ 変数分離形の微分方程式としても解釈できる問題を，変数分離形として解く場合と，全微分方程式として解く場合とでは，別々に積分するかまとめて積分するかの違いがあります． ○ 変数分離形の微分方程式を変数分離形として解く場合には
ただし，行きがかり上
g(y)dyではなく
=f(x)g(y)をG(y)と定義 していることに注意 という問題は =f(x)dx =f(x)dx ここで =G(y) , f(x)dx=F(x)とおくと G(y)=F(x)+C1…(A) という形で「各々の積分を別々に求めている」ことになります． ○ 同じ問題を全微分方程式として解く場合には f(x)dx+(−)=0 f(x)dx=F(x) , =G(y)とおくと Z(x,y)=F(x)−G(y)という関数について =f(x) , =−になっているから 全微分方程式は dz=dx+dy=0 になり，一般解は F(x)−G(y)=C2…(B) になります． ○ (A)と(B)はC2=−C1とすれば同じものを表しています． |
|
【問題１】
次の微分方程式は完全微分形になっています． 積分形F(x,y)の見当をつけて一般解を求めてください． y3dx+3xy2dy=0 1x+y3=C 23x+y2=C 3xy3=C 4x2y3=C HELP
F(x,y)=xy3とおくと
=y3 , =3xy2になるから xy3=C→3 |
【問題２】
次の微分方程式は完全微分形になっています． 積分形F(x,y)の見当をつけて一般解を求めてください． (y+2x)dx+xdy=0 1x+y2=C 2xy+x2=C 32xy=C 4x2y=C HELP
F(x,y)=xy+x2とおくと
=y+2x , =xになるから xy+x2=C→2 |
|
■完全微分形であるための必要十分条件
(1)の証明(1) 全微分方程式 P(x,y)dx+Q(x,y)dy=0 が完全微分形となっているための必要十分条件は = が成立することである． (2) P(x,y)dx+Q(x,y)dy=0 が完全微分形であるとき，その一般解は P(x,y)dx+  Q(x,y)−P(x,y)dx dy=Cで求められる． (3)は下に分けて示す． 完全微分形ならば，ある関数F(x,y)が存在して =P(x,y) , =Q(x,y) が成り立つはずです． ここで扱っている関数は，連続で微分可能なものばかりを想定しているので，偏微分の順序交換が可能です．すなわち， = が成り立ちます．したがって =()= =()= の２つは等しく = が成り立ちます．■ 逆に， = が成り立つとき，完全微分形であることは次のようにして示されます． F(x,y)=P(x,y)dx+C とおく．ここで，通常ならばCは任意定数ですが，xで偏微分したときに消えるためにはyの関数であってもよいので，C(y)とします．すなわち F(x,y)=P(x,y)dx+C(y)…(A) このC(y)を次の条件を使って求めとよい． =Q(x,y)…(B)
(A)と(B)の条件を満たせば，完全微分形になることが言えます．
(A)を(B)に代入すると(A)により =P(x,y) (B)により =Q(x,y) したがって，与えられた全微分方程式の左辺はF(x,y)の全微分になっています．･･･■(1)の証明完了 P(x,y)dx+C'(y)=Q(x,y) C'(y)=Q(x,y)−P(x,y)dx C(y)= Q(x,y)−P(x,y)dxdy以上をまとめると F(x,y)=P(x,y)dx+ Q(x,y)−P(x,y)dxdyしたがって，一般解は P(x,y)dx+ Q(x,y)−P(x,y)dxdy=C･･･■(2)が示された |
○ ここまでに示した例では，全微分方程式が完全微分形になっている場合を取り上げましたが，いつもそうであるとは限りません． 与えられたP(x), Q(x)が少し変わるだけで完全微分形になるかどうかが変わります． 【例】 (1.1)(3x2y2)dx+(2x3y)dy=0 → ○（完全微分形） (1.2)(3xy2)dx+(2x2y)dy=0 → ×（完全微分形ではない） (1.3)(3x3y2)dx+(2x4y)dy=0 → ×（完全微分形ではない） 【例】 (2.1)y3dx+3xy2dy=0 → ○（完全微分形） (2.2)y2dx+3xydy=0 → ×（完全微分形ではない） (2.3)y4dx+3xy3dy=0 → ×（完全微分形ではない） そこで，全微分方程式を解くためには，次の点が重要になります． (1) 与えられた全微分方程式が完全微分形であるかどうかを見分ける方法
⇒完全微分形になっていれば，上で練習したような積分F(x,y)を見つけられる可能性がありますが，そうでなければ探す努力が無駄になるからです
(2) 完全微分形である場合の一般解の求め方
⇒ここまでに示したものは比較的簡単に積分F(x,y)が見つけられるものばかりでしたが，複雑な式になるともっと系統的に見つける方法がないと対応できません
(3) 完全微分形でないときに，微分方程式の両辺に掛ければ完全微分形に変形できるような因子M(x,y)の見つけ方
⇒1.2や1.3を1.1に変形するには，各々の両辺にM(x,y)=x, 1/xを掛ければよい.
2.2や2.3を2.1に変形するには，各々の両辺にM(x,y)=y, 1/yを掛ければよい. このように，全微分方程式の両辺に適当な関数M(x,y)を掛ければ全微分形にできるとき，M(x,y)は積分因子と呼ばれます．この積分因子の見つけ方が分かれば全微分方程式が解けることになります．
【例題３】
（解答）微分方程式(2x−3y)dx+(4y−3x)dy=0を解いてください． ○ 完全微分形であることを確認する (2x−3y)=−3 (4y−3x)=−3 の２つが等しいから，完全微分形になっている． ○ 一般解を求める P(x,y)dx=(2x−3y)dx=x2−3xy Q(x,y)−P(x,y)dx=(4y−3x)−(−3x)=4y Q(x,y)−P(x,y)dxdy=4ydy=2y2ゆえに x2−3xy+2y2=C…（答）
【例題４】
（解答）微分方程式2xydx+(x2−2y)dy=0を解いてください． ○ 完全微分形であることを確認する (2xy)=2x (x2−2y)=2x の２つが等しいから，完全微分形になっている． ○ 一般解を求める P(x,y)dx=2xydx=x2y Q(x,y)−P(x,y)dx=(x2−2y)−x2=−2y Q(x,y)−P(x,y)dxdy=(−2y)dy=−y2ゆえに x2y−y2=C…（答） |
|
○ はじめに完全微分形であることを確かめる
=1 , =1 だから，完全微分形である． ○ 一般解を求める P(x,y)dx=(2xy+y)dx=x2+xy Q(x,y)−P(x,y)dx=x−x=0 Q(x,y)−P(x,y)dxdy=0dy=0ゆえに x2+xy=C→1 |
【問題４】
微分方程式(2x+3y)dx+(3x−2)dy=0の一般解を求めてください． 1x2−3xy+2y=C 2x2+3xy−2y=C 3x2−2xy+3y2=C 4x2+2xy−3y2=C HELP
○ はじめに完全微分形であることを確かめる
−=3−3=0 だから，完全微分形である． ○ 一般解を求める P(x,y)dx=(2x+3y)dx=x2+3xy P(x,y)dx=(x2+3xy)=3x Q(x,y)−P(x,y)dx=3x−2−3x=−2 Q(x,y)−P(x,y)dxdy=(−2)dy=−2yゆえに x2+3xy−2y=C→2 |
【問題５】
微分方程式(siny−sinx)dx+xcosydy=0の一般解を求めてください． 1xsiny+cosx=C 2ysinx+cosx=C 3xcosy−sinx=C 4ycosx−siny=C HELP
○ はじめに完全微分形であることを確かめる
−=cosy−cosy=0 だから，完全微分形である． ○ 一般解を求める P(x,y)dx=(siny−sinx)dx=xsiny+cosx P(x,y)dx=(xsiny+cosx)=xcosy Q(x,y)−P(x,y)dx=xcosy−xcosy=0 Q(x,y)−P(x,y)dxdy=0dy=0ゆえに xsiny+cosx=C→1 |
○ はじめに完全微分形であることを確かめる
−=ex−ex=0 だから，完全微分形である． ○ 一般解を求める P(x,y)dx=(yex)dx=yex P(x,y)dx=(yex)=ex Q(x,y)−P(x,y)dx=ex−cosy−ex=−cosy Q(x,y)−P(x,y)dxdy=(−cosy)dy=−sinyゆえに yex−siny=C→3 |
|
(3) ■積分因子の利用
P(x,y)dx+Q(x,y)dy=0
が完全微分形でなくても，適当な関数M(x,y)を掛けると M(x,y)P(x,y)dx+M(x,y)Q(x,y)dy=0 が完全微分形になることがあります． このときM(x,y)を積分因子といいます．
積分因子を一般的に求めるのは難しく，積分因子がただ１通りに定まるとも限りません．
（解説）しかし，積分因子M(x,y)がxだけの関数になっているものM(x)やyだけの関数になっているものM(y)があれば，次のようにして求められます． 積分因子が１つでも見かれば，それを使って解けばよいので，yだけの関数になっているものM(y)はM(x)が求まらないときに考えればよいでしょう． もし，元の全微分方程式 P(x,y)dx+Q(x,y)dy=0 が完全微分形でなければ −≠0…(4) このとき， [1] もしxだけの関数になっているものM(x)が積分因子になっていれば (M(x)P(x,y))−(M(x)Q(x,y))=0…(5) M(x)はxだけの関数としているから，(5)は次のように変形できる．
左のように未知の関数M(x)を既知の関数P(x,y) , Q(x,y)で表して，M(x)を求めていく
M−(M'Q+M)=0M(−)=M'Q (−)=…(6)
【重要】 この(6)式において，左辺がxだけの関数になっていれば，以下のように変形して積分因子M(x)が求められます．しかし，左辺がxだけの関数になっていなければ，（右辺はxだけの関数なので）この形で求めることはできないと判断します．
(−)dx=dx=logM(x)…(7)指数・対数の関係：x=log M ⇔ ex=M により，(6)式の左辺を計算しておいて（□とする） M(x)=e□ とすれば，積分因子M(x)が求まったことになります．右へ続く→ |
[1]の手順でxだけの関数になっている積分因子M(x)が求まらないときは，同様の手順でyだけの関数になっているものM(y)を探すことになります．
[2] もしyだけの関数になっているものM(y)が積分因子になっていれば(M(y)P(x,y))−(M(y)Q(x,y))=0…(5') M(y)はyだけの関数としているから，(5')は次のように変形できる． (M'P+M)−M=0 M(−)=M'P (−)=…(6')
【重要】 この(6')式において，左辺がyだけの関数になっていれば，以下のように変形して積分因子M(y)が求められます．
(−)dy=dy=logM(y)…(7')指数・対数の関係：x=log M ⇔ ex=M により，(6)式の左辺を計算しておいて（□とする） M(y)=e□ とすれば，積分因子M(y)が求まったことになります． [3] xだけの関数となる積分因子，yだけの関数となる積分因子がいずれも見つからない場合でも，P(x,y) , Q(x,y)が多項式である場合には，M(x,y)=xmynとおいて，次数m, nに関する方程式として係数比較法で解ける場合があります．
下記の【例題６】において求める積分因子をM(x,y)=xmynとおくと，次のようにして次数m, nが定まります．
xmynydx+xmyn(2x+y)dy=0 xmyn+1dx+(2xm+1yn+xmyn+1)dy=0 =(n+1)xmyn =2(m+1)xmyn+mxm−1yn+1 これらが等しくなるためには， m=0, n+1=2m+2 → m=0, n=1 したがって，M(x,y)=yが積分因子 |
|
【例題５】
（解答）(x+y2+1)dx+2y dy=0について，積分因子を求めて微分方程式を解いてください． P(x,y)=x+y2+1 , Q(x,y)=2yとおくと −=2y−0=2y は０にならないから，元の微分方程式は完全微分形ではない． xだけの関数になっている積分因子M(x)があるとすると (−)dx=2y dx=dx x=log M(x)より 積分因子はM(x)=ex これを掛けると ex(x+y2+1)dx+2yexdy=0 が完全微分形になるので，これを解く． 改めて，P(x,y)=ex(x+y2+1) , Q(x,y)=2yexとおくと I=Pdx=ex(x+y2+1)dxとおくと
I=ex(x+y2+1)−exdx =ex(x+y2+1)−ex=ex(x+y2) P(x,y)dx=2yex Q(x,y)−P(x,y)dx=2yex−2yex=0 Q(x,y)−P(x,y)dxdy=(0)dy=0ゆえに ex(x+y2)=C |
【例題６】
（解答）ydx+(2x+y)dy=0について，積分因子を求めて微分方程式を解いてください． P(x,y)=y , Q(x,y)=2x+yとおくと −=1−2=−1 は０にならないから，元の微分方程式は完全微分形ではない． そこで積分因子を求める． (−)=はxだけの関数ではない． (−)=はyだけの関数になっている． (−)dy=dy=log y log y= log M(y)より M(y)=yが積分因子 これを掛けると y2dx+(2xy+y2)dy=0 が完全微分形になるので，これを解く． 改めて，P(x,y)=y2 , Q(x,y)=2xy+y2とおくと Pdx=xy2 Q(x,y)−P(x,y)dx=2xy+y2−2xy=y2 Q(x,y)−P(x,y)dxdy=したがって xy2+=C1 3xy2+y3=C…（答） |
||||||||
|
※それぞれ積分因子を求めて微分方程式を解いてください．
P(x,y)=1+xy , Q(x,y)=x2とおくと
=x , =2x (−)==− はxだけの関数だから積分因子M(x)が存在する． (−)dx=−dx=−log x=log log=log M(x)より M(x)=が積分因子 ○ 積分因子を掛けて完全微分形の方程式にする． (+y)dx+xdy=0 改めて，P(x,y)=+y , Q(x,y)=xとおくと P(x,y)dx=log x+xy P(x,y)dx=x Q(x,y)−P(x,y)dx=x−x=0 Q(x,y)−P(x,y)dxdy=(0)dy=0ゆえに log x+xy=C→3 |
P(x,y)=y , Q(x,y)=y−xとおくと
=1 , =−1 (−)=はxだけの関数でない (−)=はyだけの関数 だからyだけの関数となる積分因子M(y)が存在する． (−)dy=−dy=−2log y=log log=log M(y)より M(y)=が積分因子 ○ 積分因子を掛けて完全微分形の方程式にする． dx+(−)dy=0 改めて，P(x,y)= , Q(x,y)=−とおくと P(x,y)dx= P(x,y)dx=− Q(x,y)−P(x,y)dx=−−(−)= Q(x,y)−P(x,y)dxdy=dy=log yゆえに +log y=C→2 ※１ この問題は，同次形の微分方程式として解くこともできます．また，積分因子をM(x,y)=xmynとおいて，次数m, nに関する方程式として係数比較法で解くこともできます．m=0 , n=−2 |
||||||||
|
【問題９】
微分方程式(x2+2x−y2)dx−2ydy=0の一般解を求めてください． 1e−x(x2+y2)=C 2ex(x2+y2)=C 3e−x(x2−y2)=C 4ex(x2−y2)=C HELP
P(x,y)=x2+2x−y2 , Q(x,y)=−2yとおくと
=−2y , =0 (−)==1はxだけの関数 だからxだけの関数となる積分因子M(x)が存在する． (−)dx=dx=x x=log M(x)より M(x)=exが積分因子 ○ 積分因子を掛けて完全微分形の方程式にする． ex(x2+2x−y2)dx−2exydy=0 改めて，P(x,y)=ex(x2+2x−y2) , Q(x,y)=−2exyとおくと I=P(x,y)dx=ex(x2+2x−y2)dxとおく 次のように２回の部分積分で求めることができます．
I=ex(x2+2x−y2)−Jとおく
I=ex(x2+2x−y2)−2xex=ex(x2−y2) P(x,y)dx=−2yex Q(x,y)−P(x,y)dx=(−2yex)−(−2yex)=0 Q(x,y)−P(x,y)dxdy=(0)dy=0ゆえに ex(x2−y2)=C→4 |
P(x,y)=x2y2−y , Q(x,y)=−xとおくと
=2x2y−1 , =−1 (−)==−2xyはxだけの関数ではない (−)=はyだけの関数ではない しかし，P(x,y), Q(x,y)が多項式であるから，M(x,y)=xmynの形の積分因子を調べる余地がある． xmyn(x2y2−y)dx−xmynxdy=0 の形の微分方程式について， 改めてP(x,y)=xmyn(x2y2−y) , Q(x,y)=−xm+1ynとおき = の条件を満たすようにm, nを定める． =(n+2)xm+2yn+1−(n+1)xmyn =−(m+1)xmyn だからn+2=0, −(n+1)=−(m+1) → m=n=−2 M(x,y)=が積分因子となる． ○ 積分因子を掛けると完全微分形の方程式になるので，これまでと同様の方法で解けばよい． （途中経過省略） x+=C→3 |
..高卒〜大学数学のメニューに戻る
...メニューに戻る