|
「作図」とは,①「定規」と②「コンパス」を使って③「有限回」の操作で,条件を満たす図形を描くことです.
(0) 「作図」では,分度器を使って角度を測ったり,ものさしを使って長さを測ることはできません.
今日では,作図ソフト,CADなど便利なものが沢山ありますが,作図では,古代ギリシヤのユークリッド幾何学の伝統に沿って,定規とコンパスだけという限られた手段を使って図形を描きます.
① 「定規」には目盛りは付いていないものとします.定規でできることは「2点を結ぶ直線を描くこと」です.
これは,多様な知識を数個の原始的なものから組み立てていくという手順を学習することが主な目的だからです. だから,目盛りの付いたものさしで長さを測ったり,分度器で角度を測るような,応用的な道具を使わずに,円と直線だけというルールで平面図形を組み立てる手順を考えるゲームだと思えば分かりやすいでしょう.
この教材の管理人の手持ちの書物には,定規ではなく定木と書かれているものが幾つかありますが,定規と書けば目盛りの付いたものさしを思い浮かべますので,目盛りはないということをはっきりさせるために定木という漢字を使っていることがあります.
② 「コンパス」は「円を描いたり」「同じ長さの線分を作る」のに使えます.
ただし,中学校数学の教科書はすべて定規という表記になっていますので,この教材でも定規にそろえます.
** 禁止されていることの例 **
なお,参考書の中には「三角定規」と「コンパス」と書かれているものもありますが,市販の三角定規は2つ1組で,30°, 45°, 60°, 90°の角が付いており,2つ組み合わせると平行線も自由に引くことができますが,この意味での三角定規ではありません.中学生が親しみやすいものとして三角定規と書かれているだけで,直角を使ったり,連携プレイすることなどは許されず,単に1本の直線が引ける板のことです.2つの三角定規を使った「平行線の引き方」 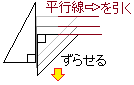 ⇒ 「作図」では,このような連携プレイは禁止されている
小学校の頃に使っていたコンパスは,ネジの部分がグラグラで,1回転すると半径がずれているような場合もありましたが,中心は動かず半径は固定できるちゃんとしたコンパスを想定します.
③ 「有限回」の操作ということは,中学校の教科書でははっきりとは書かれていません.中学校では無限とは何かということを教えていないし,まさか無限回行う中学生はいないから,書かなくても分かるはずだということかもしれませんが,実際には有眼回の操作でなければなりません.
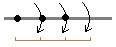 半径が固定できるので,中心を別の場所に移してちょいと回すと,同じ長さの線分が幾らでも描けることになります.
半径が固定できるので,中心を別の場所に移してちょいと回すと,同じ長さの線分が幾らでも描けることになります.
例えば,作図の単元が終わるまでには「角の三等分線を作図することはできない」という定理を紹介してもらうことがあるでしょう.
しかし,次のようにすれば描けるのです. というように,次々に1/4倍にした分数の和を考えると |
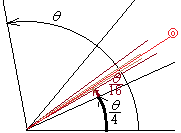 左の式を参考にして,角の四等分線を次々に作っていくとその和が三等分線になります.
左の式を参考にして,角の四等分線を次々に作っていくとその和が三等分線になります.角θの四等分線を描き,さらに,その四等分を繰り返すと角の16等分線,64等分線,…が次々と描けます. 右図のように,それらを足したものが「角の3等分線」です. ただし,この手順は「作図」という観点から言えば反則です.なぜなら,「有限回の操作」で終わらずに「無限回」の操作を行っているからです. この例から分かるように,作図は有限回の操作でできるものでなければならないということです. 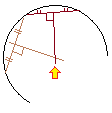 (常識感覚と作図の前提とは違うことを示す例)
(常識感覚と作図の前提とは違うことを示す例)※1 例えば,右図のように「円の一部(弧)または全部が描かれていて中心が描かれていない図において,中心を作図せよ」という問題があるときに,「目分量でそれらしく引いたら,直接に引けるじゃないか?」と思うかもしれませんが,それは正確な「作図」とは言えません. 正しく作図するには,弦の垂直二等分線を2つ描き,それらの交点を円の中心とすればよいでしょう. なぜなら,弦の垂直二等分線の交点は円の中心となるからです. 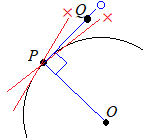 ※2 例えば,「円周上の1点Pが与えられているときに,その点を通る接線を作図せよ」という問題があるとき「目分量でそれらしく引いたら,直接に引けるじゃないか?」と思うかもしれませんが,
※2 例えば,「円周上の1点Pが与えられているときに,その点を通る接線を作図せよ」という問題があるとき「目分量でそれらしく引いたら,直接に引けるじゃないか?」と思うかもしれませんが,右図の×印で示したように,単なる線なら引けますが,半径に垂直でなければ接線とは言えません.だから,作図の手順としては,「①初めに円の中心を作図し」「②次に点Pを通って半径に垂直な直線上の1点Qを求めてから」「③直線PQを引く」という手順を踏まなければなりません. なぜなら,”2点が決まらないと直線は決まらない”からです.
【要約】
(1) 作図では,「定規」と「コンパス」を「有限回」使って,条件を満たす図形を描く (2) 「定規」を使えば,「2点を結ぶ直線が引ける」 (3) 「コンパス」を使えば「円」が描け,「同じ長さの線分が作れる」 |
[線分の垂直二等分線の作図] 【例題1】
【例題1】右図の線分ABの垂直二等分線を作図してください. 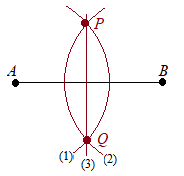 (解答)
(解答)(1) 点Aを中心とする円を描く. (2) (1)のときと半径を変えずに,点Bを中心とする円を描く. (3) (1)(2)でできる2つの交点P, Qを結ぶ直線を引くと,線分ABの垂直二等分線になる.
(1)(2)において,円を描くときに半径は適当に決めればよいが,1つだけ条件があります.
(1)で描いた円弧と(2)で描いた「円弧が交わるように,そこそこの長さの半径(=ABの半分よりは大きいもの)」でなければなりません. 「適当に」とか「そこそこの長さ」といった不安定な決め方では気持ちが悪いので,「ABを半径として」というように明確に決めてほしいと思うかもしれませんが…「ABを半径として」円を描くと1つの正しい作図になりますが,他の長さでもよいということは忘れないように. (1)(2)の半径は,理論上はどんなに長くてもかまいませんが,実際上はあまりに長いと,コンパスを幾ら開いても届かないとか,答案用紙の中に円が描けないとかの不都合がありますので,そこそこの長さに押さえておかなければなりません…これはやってみれば分かるはずです.
(1)と(2)はどちらが先でもよいが,(3)は必ず(1)(2)よりも後でなければなりません.2つの交点P, Qが決まらないと,直線が引けないからです.
 (備考)
(備考)作図の単元は中学校1年生の教科書にあります.これに対して,証明の進め方は中学校2年生で習いますので,中学1年生の段階ではまだ習っていないことになります. そこで,中学校の作図においては「作業の手順が正しければよく」「求められている作図が,その手順でできることの証明はいらない」という立場で採点します.
この例題で示した作図の手順によって垂直二等分線が描ける訳は,次の通りです.
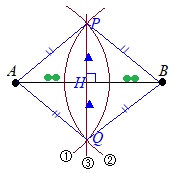
(1)(2)で半径を変えていないから,右図においてAP =AQ =BP =BQになります.4辺の長さが等しい4角形は「ひし形」で,ひし形においては「対角線は互いに他を垂直に二等分する」という性質があります. だから,AH=BHかつAB⊥PQとなります. |
【類題1】
【例題1】の解答において,(1)の円の半径と(2)の円の半径を変えた場合,(3)でできる直線PQはどんな直線になりますか. 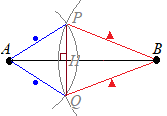 (解答)
(解答)右図のように,AP=AQで△APQは二等辺三角形になり, BP=BQで△BPQも二等辺三角形になります. △AQBを直線ABで折り返すと△APBに重なるから,PQはABの垂線になります. ABはPQの垂直二等分線になりますが,PQはABに対する垂線ではあるが二等分線にはなりません.
以上の類題と元の例題を比較してみると,例題において
[垂直二等分線の応用問題]AP=AQ, BP=BQ…(*1) が成り立つことは,PQがABに垂直となるための条件で さらに AP=BP, (AQ=BQ)…(*2) も追加すると,PQがABを二等分することになります.
【三角形の外心(外接円の中心)の作図】
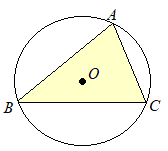
与えられた△ABCの外接円の中心(外心)Oを作図するには,2つの垂直二等分線を描くとできます.
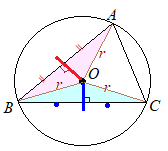 (解説)
(解説)△ABCの外接円の中心(外心)をOとすると, OA=OB=OC=r(半径) が成り立ちます.したがって,△OAB, △OBC, △OCAは,いずれも二等辺三角形になります. 「二等辺三角形の底辺の垂直二等分線は頂点を通る」ので,右図において
(1) ABの垂直二等分線を引く(赤線で示した)
(2) BCの垂直二等分線を引く(青線で示した) (3) (1)(2)の交点がそれぞれの二等辺三角形の頂点,すなわち外接円の中心になります.
*** CAの垂直二等分線は引かなくてよい.***
そもそも「△ABCの3辺の垂直二等分線は1点で交わる.この点を△ABCの外心という.」となっているので,CAの垂直二等分線は,AB, BCの垂直二等分線の交点を通ります. だから,3本目の垂直二等分線を引かなくてもよいのです.(この意味では,どれか2本,例えばAB, CAの垂直二等分線の交点を求めると,BCの垂直二等分線は引かなくてもよいとも言えます) |
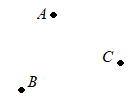 【問題1.1】
【問題1.1】右の図で,3点A, B, Cを通る円の中心Oを,定規とコンパスを使って作図せよ。なお,作図に用いた線も残しておくこと。 (鹿児島県1999年入試問題)
 (作図の仕方)
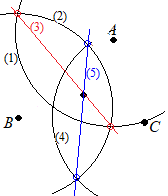
(作図の仕方)
(1) Aを中心とする円を描く
(2) Bを中心とする円を描く (3) (1)(2)の2交点を結んでABの垂直二等分線を引く (4) Cを中心とする円を描く (5) (2)(4)の2交点を結んでBCの垂直二等分線を引く (6) AB, BCの垂直二等分線の交点が△ABCの外接円の中心(外心)Oとなる |
 【問題1.2】
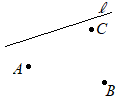
【問題1.2】右図のように,3点A, B, Cと直線lがある。直線l上にあって,∠ACB =∠APBとなる点Pを定規とコンパスを使って1つ作図せよ。なお,作図に用いた線は消さずに残しておくこと。 (熊本県2000年入試問題)
(考え方)
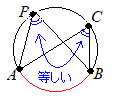 ○中学校2年生で習う円周角の定理によれば,「同じ弧に対する円周角は等しい」.
○中学校2年生で習う円周角の定理によれば,「同じ弧に対する円周角は等しい」.○円周角の定理の逆も成り立ち,「2点C, Pが直線A, Bの同じ側にあって,∠ACB =∠APBならば4点A, B, C, Pは同一円周上にある」といえる. ○そこで,3点A, B, Cを通る円と直線lの交点を求めたらよい.3点A, B, Cを通る円とは,△ABCの外接円のことであるから,△ABCの外接円の中心,すなわち外心を作図すればよい. そのためには,線分ABの垂直二等分線と線分BCの垂直二等分線の交点を求めたらよい. 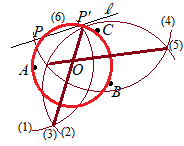 (解答)
(解答)
(1) Aを中心とする円を描く
(2) Bを中心とする円を描く (3) (1)(2)の2交点を結んでABの垂直二等分線を引く (4) Cを中心とする円を描く (5) (2)(4)の2交点を結んでBCの垂直二等分線を引く (6) AB, BCの垂直二等分線の交点を△ABCの外接円の中心(外心)Oとする (7) Oを中心として,半径がOAの円を描き,直線lの交点が求める点直線Pである.
この問題では,「1つ作図せよ」となっているが,点Pは2つある.この場合,上の図のように2つ描いたらどうなるか?…おそらく,作図の手順が理解できているかどうかを調べるのが採点の核心なので,少なくとも1つ書いてあればよいと考えられる.筆者が採点官である場合は,上記のように2つとも描いてしまっても減点はしない.
|
 【問題1.3】
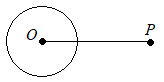
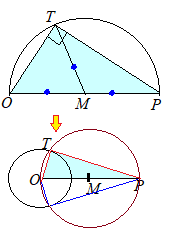
【問題1.3】右図において,線分OPの中点Mを作図し,それを用いて点Pから円Oにひいた2本の接線を作図しなさい。ただし,作図に用いた線を消さないこと。 (島根県2000年入試問題)
 (考え方)
(考え方)中学校2年生で習う円周角の定理のうちで,特に「直径の上に立つ円周角は90°になる」というものがあります. この定理によれば,右図のように,点Mを中心として,OPを直径とする円があるときに,円周上の任意の点をTとすると,∠OTP =90°になります. そこで,点Mを中心として,OM=MP (=r)を半径とする円と円点Oとの交点をTとすると,∠OTP=90°となって,TPが半径OTに垂直な直線,すなわち接線になります.
この問題では,中点Mの作図という初歩的な誘導問題があり,ほとんどの受験生はここまではできるはずです.
しかし,その後で間違ってMから接線を引こうと考えてしまって,正解に達しない人が相当数あるかもしれません. 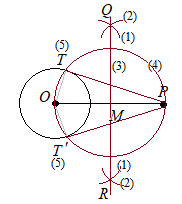 (解答)
(解答)
(1) Oを中心とする円を描く
右図のように,OPの半分よりも大きな半径にする
(2) (1)と半径の長さを変えずにPを中心とする円を描く(3) (1)(2)の2交点を結んでOPの垂直二等分線を引き,OPとの交点をMとする (4) Mを中心とし,半径MP (=MO)の円を描き,円Oとの交点をT, T'とする (5) TP,T'Pが求める接線になる. |
 【問題1.4】
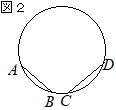
【問題1.4】右の図2において,線分ABとCDは円の弦である。円の中心Oを定規とコンパスを用いて図2に作図して求め,その位置を•で示せ。ただし,作図に用いた線は消さずに残しておくこと。 (長崎県2015年入試問題)
(考え方)
線分ABと線分CDの垂直二等分線の交点を求めたらよい. (作図) 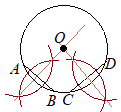 (1) 点Aを中心として円をく.
(1) 点Aを中心として円をく.(2) (1)のときと半径を変えずに,点Bを中心とする円を描く. (3) (1)(2)の2交点を結ぶ直線を引く. (4) 点Cを中心として円をく. (5) (4)のときと半径を変えずに,点Dを中心とする円を描く. (6) (4)(5)の2交点を結ぶ直線を引き,(3)と交わる点をOとする. |
 【問題1.5】
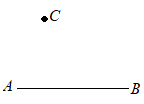
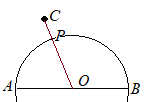
【問題1.5】右の図のように,線分ABと,線分AB上にない点Cがある。ABを直径とする円の周上にあって,Cからの距離が最も短くなる点Pを,定規とコンパスを使って作図しなさい。なお,作図に用いた線は消さずに残しておくこと。 (熊本県2015年入試問題)
 (考え方)
(考え方)ABを直径とする円周上に点Pを描けば,CPが最短になります. そこで,ABの垂直二等分線を作図して,ABの中点を求めて,これを円の中心とすればよい。 (作図) 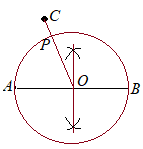 (1) 点Aを中心として円をく.
(1) 点Aを中心として円をく.(2) (1)のときと半径を変えずに,点Bを中心とする円を描く. (3) (1)(2)の2交点を結ぶ直線を引き,ABとの交点を円の中心Oとする. (4) Oを中心として,半径OAの円を描く. (5) (4)の円と線分COとの交点をPとする. |
 【問題1.6】
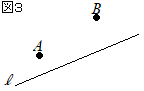
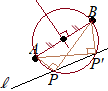
【問題1.6】図3において,直線l上にあって,∠APB=90°となる点Pを定規とコンパスを用いて図3に作図して求め,その位置を•ですべて示せ。ただし,作図に用いた線は消さずに残しておくこと。 (長崎県2017年入試問題)
 (考え方)
(考え方)中学校2年生で習う円周角の定理のうちで,特に「直径の上に立つ円周角は90°になる」というものがあります. また,その逆,すなわち「円周角が90°になるなら,その弦は直径である」も成り立ちます. そこで線分ABを直径とする円と直線lの交点をPとすると,∠APB=90°になります.(このような点Pは一般には2つあります.) ABを直径とする円を描くには(円の中心を求めるには),ABの垂直二等分線を描いて,ABの中点を円の中心とすればよい. (作図) 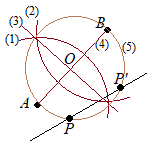 (1) 点Aを中心として円をく.
(1) 点Aを中心として円をく.(2) (1)のときと半径を変えずに,点Bを中心とする円を描く. (3) (1)(2)の2交点を結ぶ直線を引く. (4) 直線ABを引き,(3)の直線との交点を円の中心Oとする. (5) Oを中心として,半径OAの円を描き,直線lとの2交点を点P, P'とする. |
 【問題1.7】
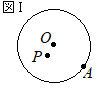
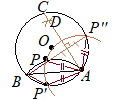
【問題1.7】図Ⅰにおいて,円Oは半径2cm の円であり,点Aは円Oの周上の点,点Pは円の内部の点で,AP=2cm である。 図Ⅰを用いて,図Ⅱのように,点Aを一端とする線分で弧が点Pに重なるように円の一部を折り返す。この折り目を線分ABとするとき,次の(1)(2)の問いに答えなさい。 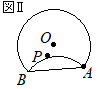 (1) 点Aを一端とする線分で円の一部を折り返すとき,弧が点Pに重なるような折り目は,線分ABのほかにもう1つある。その折り目を線分ACとするとき,線分ACをコンパスと定規を用いて作図しなさい。
(1) 点Aを一端とする線分で円の一部を折り返すとき,弧が点Pに重なるような折り目は,線分ABのほかにもう1つある。その折り目を線分ACとするとき,線分ACをコンパスと定規を用いて作図しなさい。ただし,作図に用いた線は消さないこと。 (2) 略 (群馬県2015年入試問題)
|
 (考え方)
(考え方)弧 逆に,円周上の点P”について,AP =AP”あれば,PP”の垂直二等分線ACで折り返すと,P”はPに重なることになります.
Aを中心として,半径APの円を描けば,もう1つの交点P”が得られます.
(作図)この問題では,AP=2cm で,AO=2cm なので,その円はたまたまOも通りますが,この事情は(1)の問題を解く上では関係ありません. (1) 点Aを中心として,半径APの円を描き,元の円との交点でB側でない方をP”とおく. (2) 点Pを中心とする円を描く. (3) (2)と半径を変えずにP”を中心として円を描き,(2)との交点をDとおく. (4) 直線ADを引き,元の円との交点をCとおく. |
[直線外の1点から垂線を引く] 【例題2】
【例題2】直線l上にない1点Aがあるとき,点Aを通ってlに垂直な直線を作図してください. 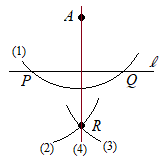 (解答)
(解答)(1) 点Aを中心として円を描き,直線lと交わる点をP, Qとおく. (2) (1)のときと半径を変えずに,点Pを中心とする円を描く. (3) (1)のときと半径を変えずに,点Qを中心とする円を描く. (4) Aと(1)(2)の交点Rを結ぶ直線を引くと,直線lの垂線になる. 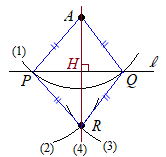 (理由)
(理由)右図において AP=AQ ←(1) AP=PR ←(2) AP=QR ←(3) 以上により,四角形APRQはひし形になり,その対角線は互いに他を垂直に二等分するから,AR⊥PQ
【類題2.1】
【例題2】の解答は,(1)~(4)の4ステップで作図していますが,これを3ステップで作図する方法を考えてください. 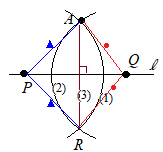 (解答)
(解答)(1) l上の1点Pを中心として半径APの円を描く. (2) l上の他の1点Qを中心として半径AQの円を描く. (3) (1)(2)の交点のうちで,直線lに関してAと反対側にある点Rと点Aを結ぶ直線を引くと,直線lの垂線になる. (理由) 右図において AP=RP ←(1) AQ=RQ ←(2) だから,直線lで折り返すと,△APQは△RPQと重なるから,AR⊥PQ |
 【問題2.1】
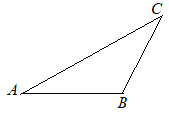
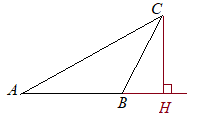
【問題2.1】右の図のように,辺ABを底辺とする△ABCがある。そのときの高さをCHとする。点Hを作図しなさい。 ただし,作図にはコンパスと定規を用い,作図に使った線は消さないこと。 (大分県2000年入試問題)
 (考え方)
(考え方)線分ABを延長した直線を描き,その直線外の1点Cを通って直線ABに垂直な線を引き,交点をHとすればよい. 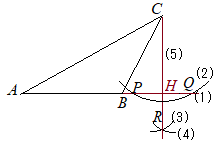 (解答)
(解答)(1) 線分ABを延長した直線を描く (2) 点Cを中心として円を描き,直線ABと交わる点をP, Qとおく. (3) 点Pを中心とする円を描く. (4) (2)のときと半径を変えずに,点Qを中心とする円を描く. (5) 点Cと(2)(3)の交点Rを結ぶ直線を引き,直線ABとの交点をHとする. 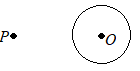 【問題2.2】
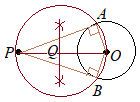
【問題2.2】右の図のように,円Oの外部に点Pがある。点Pから円Oに2本の接線をひき,接点をA, Bとする。次の1, 2の問いの答えなさい。 1 点Pから円Oにひいた2本の接線を,定規とコンパスを使って作図せよ。ただし,2点A, Bの位置を示す文字A, Bも書き入れ,作図に用いた線は残しておくこと。 2 略 (鹿児島県2017年入試問題)
 (考え方)
(考え方)接線PAは半径OAに垂直になり,接線PBは半径OBに垂直になる.
ところで,中学校2年生で習う円周角の定理のうちで,特別な場合として,「直径の上に立つ円周角は90°になる」というものがある.これを利用して,OPを直径とする円を描けば,その円周上の点A, Bは∠PAO =90°, ∠PBO =90°を満たすことになります.
OPを直径とする円を描くためには,前もってその円の中心を求めておかなければならないので,初めにOPの垂直二等分線を作図します.(解答) (1) 点Pを中心として円を描く. (2) (1)のときと半径を変えずに,点Oを中心とする円を描く. (3) (1)(2)の2つの交点を結ぶ直線とOPとの交点をQとおく. (4) 点Qを中心とし,PQを半径とする円を描き,元の円との交点をA, Bとする. (5) 直線PA, PBを引く. |
[直線上の1点から垂線を引く]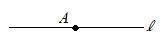 【例題3】
【例題3】直線l上の1点Aを通ってlに垂直な直線を作図してください. 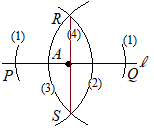 (解答)
(解答)(1) 点Aを中心として円を描き,直線lと交わる点をP, Qとおく. (2) 点Pを中心とする円を描く. (3) (2)のときと半径を変えずに,点Qを中心とする円を描く. (4) (2)(3)の2交点R, Sを結ぶ直線を引くと,直線lの垂線になる.
(2)(3)の円の半径は(1)よりも大きくなければならない.(1)以下では,2つの交点R, Sができない.
(*) この手順の中で,(2)(3)の操作を直線lよりも上の部分だけで行ってもよい.その場合は,2点R, Aを結ぶ直線が直線lの垂線になる. 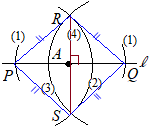 (理由)
(理由)右図において,四角形PSQRはひし形になり,その対角線は互いに他を垂直に二等分するから,AR⊥PQ
上記の(*)で示した手順で行う場合は,△RPA ≡△RQAになるから,
∠RAP =∠RAQ , ∠RAP+∠RAQ =180°から∠RAP=90°が言える. |
 【問題3.1】
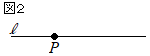
【問題3.1】図2において,点Pを通り直線lに垂直な直線を定規とコンパスを用いて作図せよ。ただし,作図に用いた線は消さずに残しておくこと。 (長崎県2017年入試問題)
(解答)
上記の【例題3】において,点Aを点Pと読み替え,P, Q, R, Sを名前が重ならないようにK, L, M, Nなどとすればよい. 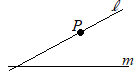 【問題3.2】
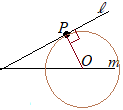
【問題3.2】右図のように,直線l上に点Pがある。 中心が直線m上にあり,直線にlに点Pで接する円Oを,定規とコンパスを用いて作図しなさい。ただし,円の中心を表す文字Oも書き,作図に用いた線は消さないこと。 (長野県2015年入試問題)
 (考え方)
(考え方)円の接線は半径と垂直になるから,点Pから直線lに垂直な線を引き,直線mとの交点を円の中心Oとすればよい. 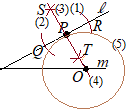 (解答)
(解答)(1) 点Pを中心として円を描き,直線lと交わる点をQ, Rとおく. (2) 点Qを中心とする円を描く. (3) (2)のときと半径を変えずに,点Rを中心とする円を描く. (4) (2)(3)の2交点S,Tを結ぶ直線を引き,直線mとの交点をOとする. (5) Oを中心として,OPを半径とする円を描く. |
[角の二等分線]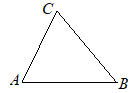 右の図の△ABCにおいて,辺BC上にあり,辺AB, ACまでの距離が等しい点Pを作図によって求めなさい。
右の図の△ABCにおいて,辺BC上にあり,辺AB, ACまでの距離が等しい点Pを作図によって求めなさい。ただし,作図には定規とコンパスを使い,作図に用いた線は消さないこと。 (栃木県2000年入試問題)
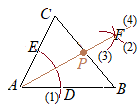 (1) 点Aを中心として円を描き,AB, ACと交わる点をD, Eとおく.
(1) 点Aを中心として円を描き,AB, ACと交わる点をD, Eとおく.(2) 点Dを中心とする円を描く. (3) (2)のときと半径を変えずに,点Eを中心とする円を描く. (4) Aと(2)(3)の交点Fを結ぶ直線を引き,BCとの交点をPとすると,Pが求める点である. |
 【問題4.1】
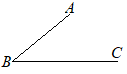
【問題4.1】右の図で,∠ABCの二等分線上に中心があり,2点A, Bを通る円を,定規とコンパスを用いて作図しなさい。 なお,作図に用いた線は消さずに残しておきなさい。 (三重県2015年入試問題)
(考え方)
角の二等分線ということは書かれているから,描いた円が2点A, Bを通るようにすることを考えるとよい. 2点A, Bを通る円の中心は,A, Bからの距離が等しい(半径になる)から,ABの垂直二等分線上にあります. 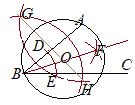 (解答)
(解答)∠ABCの二等分線を引く.
(1) 点Bを中心として円を描き,AB, ACと交わる点をD, Eとおく.
ABの垂直二等分線を描く.(2) 点Dを中心とする円を描く. (3) (2)のときと半径を変えずに,点Eを中心とする円を描く. (4) Bと(2)(3)の交点Fを結ぶ直線を引く.
(5) 点Aを中心として円を描く.
(6) (5)のときと半径を変えずに,点Bを中心とする円を描く. (7) (5)(6)の2交点G, Hを結ぶ直線を引き,(4)の直線との交点をOとする. (8) Oを中心として,OBを半径とする円を描く. |
 【問題4.2】
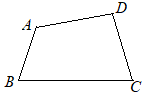
【問題4.2】右の図のように,四角形ABCDがある。辺ABが辺ADに重なるように折ったときの折り目の線と辺BCとの交点Pを,定規とコンパスを使って作図しなさい。なお,作図に用いた線は消さずに残しておくこと。 (熊本県2017年入試問題)
(考え方)
線分APで折り返して,ABとADが重なるようにするには,APが∠DABの二等分線になるようにすればよい. (作図) 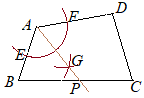 (1) 点Aを中心として円を描き,AB, ADと交わる点をE, Fとおく.
(1) 点Aを中心として円を描き,AB, ADと交わる点をE, Fとおく.(2) 点Eを中心とする円を描く. (3) (2)のときと半径を変えずに,点Fを中心とする円を描く. (4) Aと(2)(3)の交点Gを結ぶ直線を引き,BCとの交点をPとする.  【問題4.3】
【問題4.3】右の図には3つの線分が与えられている。これらの線分すべてに接する円の中心Oと,1つの接点Pを作図によって求めなさい。ただし,作図に用いた線は消さないこと。 (石川県2000年入試問題)
(考え方)
角の二等分線を描くと,2つの辺から等距離にある点(の集まりとしての直線)が描ける. 角の二等分線を2つ描いて,その交点を求めると,3つの辺から等距離にある点が得られる. (作図) 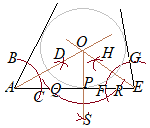 1つの角の二等分線を描く.
1つの角の二等分線を描く.
(1) 点Aを中心として円を描き,2つの辺との交点をB, Cとおく.
もう1つの角の二等分線を描く.(2) 点Bを中心とする円を描く. (3) (2)のときと半径を変えずに,点Cを中心とする円を描く. (4) Aと(2)(3)の交点Dを結ぶ直線を引く.
(5) 点Eを中心として円を描き,2つの辺との交点をF, Gとおく.
角の二等分線2つの交点が求める円の中心Oである.(6) 点Fを中心とする円を描く. (7) (6)のときと半径を変えずに,点Gを中心とする円を描く. (8) Eと(6)(7)の交点Hを結ぶ直線を引く. 次に,1つの接点Pを求める.
(9) 点Oを中心として円を描き,2つの辺との交点をQ, Rとおく.
(10) 点Qを中心とする円を描く. (11) (6)のときと半径を変えずに,点Rを中心とする円を描く. (12) Oと(6)(7)の交点Sを結ぶ直線を引き,直線AEとの交点をPとする. |
 【問題4.4】
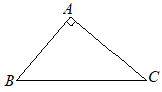
【問題4.4】∠A=90°の△ABCがある。辺AC上の点Dと頂点Bを結ぶ線分BDを折り目として頂点Aがちょうど辺BC上にくるように折り曲げた。 頂点Aが重なる辺BC上の点をEとするとき,折り目の線分BDと点Eの位置を右上の図に作図しなさい。ただし,作図に用いた線は残しておくこと。 (富山県2000年入試問題)
折り曲げて重なるということから,∠ABD=∠DBCすなわち,∠ABCの二等分線を作図すれば目途がつきます.
他方で,AB=AEとなることから,Eも円を描けば作図できます. このようにすれば,問題としては解けてしまいますが,そのように解いてしまうと∠A=90°という条件を使わずに解けたことになります.この辺の事情は後で検討することとして,とりあえず答案を書くと. 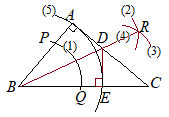 (解答)
(解答)(1) 点Bを中心として円を描き,AB, BCと交わる点をP, Qとおく. (2) 点Pを中心とする円を描く. (3) (2)のときと半径を変えずに,点Qを中心とする円を描く. (4) Bから(2)(3)の交点Rへ直線を引き,ACとの交点をDとおく. (5) Bを中心とし,ABを半径とする円を描きBCと交わる点をEとおく. 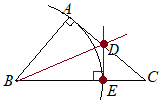 (∠A=90°という条件の検討)
(∠A=90°という条件の検討)元の問題には,∠A=90°という条件が付いています.これにより,問題が難しくなっているのではなく,(*1)上記のような作図方法だけでなく,(*2)Eから垂線を引いてDを求めたり,(*3)逆にDから垂線を引いてEを求めることもできるようになっている(より易しくなっている)と考えることができます. 教科書で重視されている流れから考えると,出題者の意図としては(*3)を想定しているように思われます.
(*3)による作図の手順
(1) 点Bを中心として円を描き,AB, BCと交わる点をP, Qとおく. (2) 点Pを中心とする円を描く. (3) (2)のときと半径を変えずに,点Qを中心とする円を描く. (4) Bから(2)(3)の交点Rへ直線を引き,ACとの交点をDとおく. (5) Dを中心として円を描き,BCと交わる点をS, Tとおく. (6) (5)のときと半径を変えずに,S, Tを中心に円を描き,Dと反対側の交点をUとおく. (7) D, Uを結ぶ直線とBCとの交点をEとおく. |
[正三角形の作図]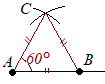 右図のように,線分ABが与えられているとき,この線分ABを1辺とする正三角形を作図するには
右図のように,線分ABが与えられているとき,この線分ABを1辺とする正三角形を作図するには
(2) Bを中心として,ABを半径とする円を描く. (3) (1)(2)の交点を第3の頂点Cとして,線分AC, BCを引くと,正三角形ABCができる.
実際には,線分ABの上側と下側に1つずつできますが,1つだけ描けばよい場合は,上記のような図になります.
なお「正三角形の1つの内角は60°」だから,正三角形の作図ができれば,60°の作図ができることになります. |
 【問題5.1】
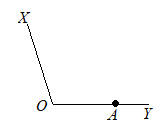
【問題5.1】右の図のように,半直線OX, OYがあり,点Aは半直線OY上の点である。半直線OX上に∠OAP =30°となる点Pを,定規とコンパスを使い,作図によって求めよ。ただし,定規は直線を引くときに使い,長さを測ったり角度を利用したりしないこととする。なお,作図に使った線は消さずに残しておくこと。 (高知県2017年入試問題)
(考え方)
正三角形の作図は上の例のようにしてできますので,まず60°が作れます.次に,その角の二等分線を引くと30°ができます. 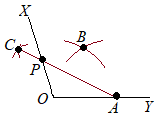 (作図)
(作図)
(1) Aを中心として,OAを半径とする円を描く.
(2) Oを中心として,OAを半径とする円を描く. (3) (1)(2)の交点をBとする. (4) Oを中心として,OBを半径とする円を描く. (5) Bを中心として,OBを半径とする円を描く. (6) (4)(5)の交点をCとし,直線ACと交点をOXの交点を交点をP/span>とする. |
 【問題5.2】
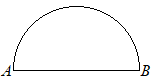
【問題5.2】右の図のように,線分ABを直径とする半円がある。 ただし,作図には定規とコンパスを用い,作図に使った線は消さないこと。 (大分県2015年入試問題)
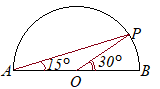 (考え方)
(考え方)前問のようにして30°の角が作れると,円周角が中心角の半分になることを利用すると15°ができます. なお,右の△PABの図は,今までに見た覚えがあると思います. 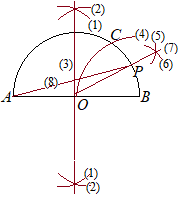 (作図)
(作図)円の中心を作図する.
(1) Aを中心として円を描く.
OBを1辺とする正三角形を描く.(2) (1)と半径を変えずにBを中心として円を描く. (3) (1)(2)の2交点を結ぶ直線とABとの交点をOとする.
(4) Oを中心として,OBを半径とする円を描く.
∠BOCの二等分線を描く.(5) Bを中心として,OBを半径とする円を描く. (6) (4)(5)の交点をCとする.
(7) Bを中心として円を描く.
APを結んだ線分を引く.
(8) (7)と半径を変えずにCを中心として円を描く. (9) (7)(8)の交点とOを結んだ直線を引き,元の円との交点をPとする. |
 【問題5.3】
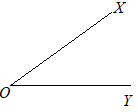
【問題5.3】右の図は∠XOYである。辺OX, OY上に3つの頂点がある正三角形ABCを,定規とコンパスを用いて作図しなさい。ただし,図をかくのに用いた線は消さないこと。 (群馬県2000年入試問題)
(考え方)
2つの辺の上に3つの頂点があるようにするには,一方に2つ,もう一方に1つあるようにしたらよい.(∠XOYは60°とは言えないから,点Oに1つの頂点をとると,正三角形にはならない) そこで,OY上に2つ,OX上に1つの頂点があるとすればよい. 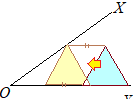 [A] OY上に底辺がある正三角形は簡単に描けるが,その頂点がOX上にあるとは限らない.そこで,できた正三角形を平行移動して,頂点がOX上にあるようにしたらよい.
[A] OY上に底辺がある正三角形は簡単に描けるが,その頂点がOX上にあるとは限らない.そこで,できた正三角形を平行移動して,頂点がOX上にあるようにしたらよい.とにかく正三角形を作り,次に平行移動する. 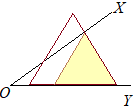 [B] OYと60°の角をなす直線が描けたら,頂点が決まり,正三角形が描ける.
[B] OYと60°の角をなす直線が描けたら,頂点が決まり,正三角形が描ける.とにかく正三角形を作り,次に拡大・縮小して相似図形にする. (作図方法[A]) 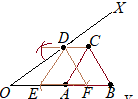 OY上に2点A, Bを選んで,ABを1辺とする正三角形を描く.
OY上に2点A, Bを選んで,ABを1辺とする正三角形を描く.
(1) Aを中心として,ABを半径とする円を描く.
CからOYに平行線を引いて,OXとの交点をDとする.
(2) (1)と半径を変えずに,Bを中心として,ABを半径とする円を描く. (3) (1)(2)の交点をCとすると,△ABCは正三角形になる.
(4) Aを中心として,ACを半径とする円を描く.
A, B, CをそれぞれCDの分だけ平行移動する.
(5) (4)と半径を変えずに,Cを中心として,ACを半径とする円を描く. (6) Cと(4)(5)の交点を結ぶ直線を引き,OXとの交点をDとする.
(7) AからCDに等しい点をEとする.
(8) BからCDに等しい点をFとする. (9) D, E, Fを結ぶと求める正三角形になる. 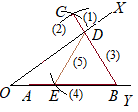 (作図方法[B])
(作図方法[B])OY上に2点A, Bを選んで,ABを1辺とする正三角形を描く.
(1) Aを中心として,ABを半径とする円を描く.
(4) Cが∠XOYの外側にあるときは,CBとOXとの交点をDとする.Cが∠XOYの内側にあるときは,CBの延長線とOXとの交点をDとする.(2) (1)と半径を変えずに,Bを中心として,ABを半径とする円を描く. (3) (1)(2)の交点をCとすると,△ABCは正三角形になる. (5) Bを中心として,BDを半径とする円とOYとの交点をEとする. (6) B, D, Eを結べば正三角形になる |
|
[正六角形の作図]
正六角形を作図してください
(学校図書の教科書 P.130参照)
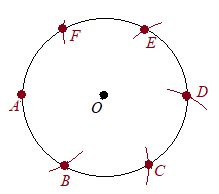 (1) 円を描く.
(1) 円を描く.(2) (1)と半径を変えずに,円周上の適当な点Aを中心として円を描き,元の円との交点をBとする. (3) 同様にしてBを中心に(1)と半径を変えずに円を描き,元の円との交点をCとする. (4) 以下同様にして,次々にD, E, Fを決める. (5) A, B, C, D, E, Fを結べば正六角形になる. 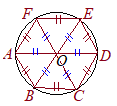 (正六角形になる理由)
(正六角形になる理由)右図において,OA, OB, OC, OD, OE, OFは初めの円の半径だから,すべて長さが等しい. また,半径を変えずに次々に描いているから,AB, BC, CD, DE, EFの長さも半径に等しい. このとき,正三角形が5つできるから,△AOFも正三角形になる. 以上により,6つの辺の長さが等しく,その内角もすべて等しい(120°)六角形になるから,ABCDEFは正六角形になる.
この方法により120°の作図もできることが分かります.
|
 【問題5.4】
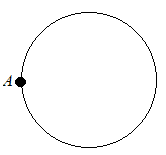
【問題5.4】右図のように,円があり,その円周上に点Aがある。 このとき,三角定規とコンパスを使って,点Aを頂点の1つとし,他の3つの頂点がいずれも,この円周上にあるような正方形を作図しなさい。 ただし,三角定規の角を利用して直線をひくことはしないものとする。また,作図に用いた線は消さずに残しておくこと。 (千葉県2000年入試問題)
 (考え方)
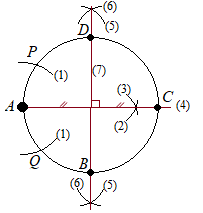
(考え方)右図のように,直径ACを描き,その垂直二等分線を描くと,正方形の対角線ができます. (解答) (1) Aを中心として円を描き,元の円との交点をP, Qとおく.
線分PQの垂直二等分線が直径になります.
(2) Pを中心として円を描く.(3) (2)と同じ半径でPを中心として円を描く. (4) (2)(3)の交点とAを結ぶ直線を描き,元の円との交点をCとする. (5) Aを中心として円を描く. (6) (5)と同じ半径でCを中心として円を描く. (7) (5)(6)の2つの交点を結ぶ直線を描き,元の円との交点をB, Dとする. (8) A, B, C, Dを結べば,求める正方形ができる. |