【例5】
次のデータは,20匹のネズミのうち,その半分は生の落花生から,他の半数は炒った落花生からタンパク質をとらせたときの摂取量を示す.落花生を炒ることがタンパク質の価値に影響を与えるかどうかを,t分布を用いて検定せよ.
| 生のもの |
61 |
60 |
56 |
63 |
56 |
63 |
59 |
56 |
44 |
61 |
| 炒ったもの |
55 |
54 |
47 |
59 |
51 |
61 |
57 |
54 |
62 |
58 |
「初等統計学」(培風館/P.G.ホーエル著/浅井晃.村上正康共訳)第4版31刷p.188,6節34.
[ポイント] 20匹のネズミがたまたま10匹ずつに分かれただけであり「生のもの」と「炒ったもの」に対応があるわけではない.したがって,対応のないt検定を行う.
(参考) 上記のデータをWeb画面上で生〜58までをドラッグ・コピーし,Excel上に単純に貼り付けると転記ミスなしに取り込むことができる.次に,Excel上でもう一度コピーし,貼り付け→行列を入れ替える ・・・・・・(1)
(Excel2002の場合は,編集→形式を選択して貼り付け→行列を入れ替える)
■Excel上でのt検定
◇◇初めにF検定を行う◇◇
まず分散が等しいと見なせるかどうかについてF検定を行う.(次のいずれか1つの方法による.)
| |
A |
B |
| 1 |
生のもの |
炒ったもの |
| 2 |
61 |
55 |
| 3 |
60 |
54 |
| 4 |
56 |
47 |
| 5 |
63 |
59 |
| 6 |
56 |
51 |
| 7 |
63 |
61 |
| 8 |
59 |
57 |
| 9 |
56 |
54 |
| 10 |
44 |
62 |
| 11 |
61 |
58 |
データは右の表の形になっているものとする.
○各々の不偏分散を求める
=VAR(A2:A11)→31.21
=VAR(B2:B11)→21.07
○分散比(大きい方÷小さい方)を求める
=31.21/21.07=1.48
[関数]
FINV(確率0.05,自由度1,自由度2)によって有意と見なせる境界値のF値が返されるのでこれよりも大きければ有意差あり,小さければ有意差なしと判断する.
FDIST(F値,自由度1,自由度2)によって分散が等しいと仮定したときにその分散比が起こる確率が返されるので,これが0.05よりも小さければ分散が等しいという帰無仮説が棄却される.
FTEST(データ1の範囲,データ2の範囲)によって2つのデータの分散が等しいと仮定したときにその分散比となる両側確率が返されるので(大きい方しか使わないので),これを2で割って上側確率が0.05よりも小さくなるかどうかを調べる.
上記の分散比(F値)と片側確率5%の境界値と比較する
=FINV(0.05,9,9)→3.18
1.48<3.18だから分散の有意差は認められない
⇒等分散とみなせる場合のt検定に進む |
=FDIST(1.48,9,9)
→0.28>0.05だから分散の有意差は認められない
⇒等分散とみなせる場合のt検定に進む |
=FTEST(A2:A11,B2:B11)
→0.5675だから上側確率は0.28
0.28>0.05だから分散の有意差は認められない
⇒等分散とみなせる場合のt検定に進む |
分析ツールを利用する場合
データ→データ分析→F検定:2標本を使った分散の検定→OK
→
| |
変数 1 |
変数 2 |
| 平均 |
57.9 |
55.8 |
| 分散 |
31.211 |
21.067 |
| 観測数 |
10 |
10 |
| 自由度 |
9 |
9 |
| 観測された分散比 |
1.482 |
|
| P(F<=f) 片側 |
0.284 |
|
| F 境界値 片側 |
3.179 |
|
右のような表が出力されるので
p片側の値が0.05よりも大きいから有意差なしと判断する.
(または観測された分散比1.482がF境界値片側3.179よりも小さいから有意差なしと判断する)
⇒等分散とみなせる場合のt検定に進む |
◇◇F検定の結果を用いてt検定を行う◇◇
[関数]
TTEST(データ1の範囲, データ2の範囲, 両側検定の場合は第3引数2とする, 等分散を仮定できるときは第4引数を2とする)によって平均値が等しいと仮定したときにそのt分布となる確率が返されるので,確率が0.05よりも小さければ有意差あり,大きければ有意差なしと判断する.
=TTEST(A2:A11,B2:B11,2,2)→0.3705
確率が0.3705>0.05だから有意差なしと判断する. |
分析ツールを利用する場合
データ→データ分析→t検定:等分散を仮定した2標本による検定→OK
| |
生のもの |
炒ったもの |
| 平均 |
57.9 |
55.8 |
| 分散 |
31.211 |
21.067 |
| 観測数 |
10 |
10 |
| プールされた分散 |
26.139 |
|
| 仮説平均との差異 |
0 |
|
| 自由度 |
18 |
|
| t |
0.918 |
|
| P(T<=t) 片側 |
0.185 |
|
| t 境界値 片側 |
1.734 |
|
| P(T<=t) 両側 |
0.371 |
|
| t 境値 両側 |
2.101 |
|
P値が0.05よりも大きいから有意差なしと判断する.(または,t値が両側境界値よりも小さいから有意差なしと判断する.) |
|
■Rコマンダーでのt検定
○ そのままのデータでは「対応のない場合のt検定」が選択できないので,右図のようにExcel上で1列に加工する(分類名A,Bで区別する.Aが生,Bが炒ったものに対応)・・・(2)
Excel上で(2)の範囲を変転表示にし,コピーし(メモリ=クリップボードに入れる.)
○ Rコマンダーのメニューで
データ→データのインポート→テキストファイルまたはクリップボード,URLから
データセット名を入力(→例えばxとする)
ファイル内に変数名あり(右図の摂取量,分類を含めてコピーしているのならチェックありのまま)
データファイルの場所(→クリップボード)
フィールドの区切り記号(→タブ)
→OK
[データセットを表示]で右図下のように表示されればよい.
○ここからがRコマンダーを用いたt検定
◇◇初めにF検定を行う◇◇
統計量→分散→分散の比のF検定
→(次の図のように選ぶ)
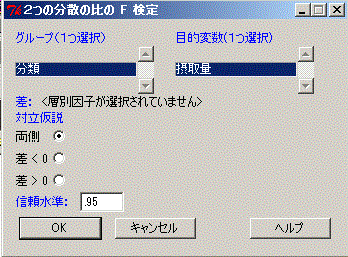
出力ウインドウに次にように出力される.
| var.test(摂取量 ~ 分類, alternative='two.sided', conf.level=.95, data=x)
F test to compare two variances
data: 摂取量 by 分類
F = 1.4815, num df = 9, denom df = 9, p-value = 0.5675
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.3679936 5.9646717
sample estimates:
ratio of variances
1.48154 |
→P値が0.05よりも大きいから有意差なしと判断する.
◇◇F検定の結果を用いてtF検定を行う◇◇
統計量→平均→独立サンプルt検定→(次の図のように選ぶ)
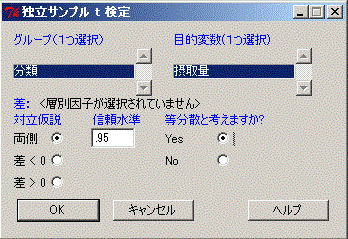
出力ウインドウに次にように出力される.
t.test(摂取量~分類, alternative='two.sided', conf.level=.95, var.equal=TRUE,
+ data=x)
Two Sample t-test
data: 摂取量 by 分類
t = 0.9185, df = 18, p-value = 0.3705
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.703618 6.903618
sample estimates:
mean in group A mean in group B
57.9 55.8 |
→P値が0.05よりも大きいから有意差なしと判断する. |
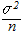
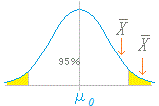
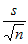 に等しい.
に等しい.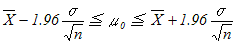
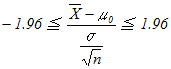
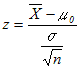
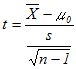 は自由度n−1のt分布になる.
は自由度n−1のt分布になる.
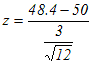 = -1.84>-1.96
= -1.84>-1.96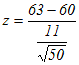 =1.92>1.645
=1.92>1.645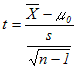 = -0.58
= -0.58
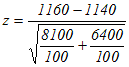 = 1.66
= 1.66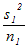 ,
,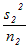 であるとき,それらの差の分散は
であるとき,それらの差の分散は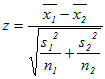 は標準正規分布をなす.
は標準正規分布をなす.