|
���`�㐔.���K�m�[�g�i�A���T�[�u�b�N�j
�@���̃y�[�W�ɂ́C���\���ꂽ���앨�i���쌠�@��32���j�̈��p���܂܂�Ă��܂��D
** �R������Ԃɂ����钼���̕����� **�@�������C�r���o�߂Ȃǂɂ́C�����앨�ɂ͂Ȃ�(���̃y�[�W�̊Ǘ��l��)���߂��܂܂�Ă��܂��D
�y�v�_�z
3������Ԃɂ����钼���̃x�N�g���������C�p�����[�^�\��(�}��ϐ��\���C���ϐ��\��)�Cxyz������
�Z3������Ԃɂ����āC�_�Z����𐬕��ŕ\���� �Z�e�����ɕ������ �Z�p�����[�^���������� 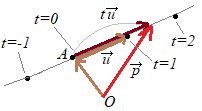 �i����j
�i����j(1)← �@�Ⴆ�C (1)�𐬕��ŏ�����(2)�܂���(3)��(3������Ԃɂ�����)�����̃p�����[�^�\��(�}��ϐ��\���C���ϐ��\��)�C�p�����[�^�������Ƃ����D (4)← (3)�̕������� �́C �����Z���w�ň����D |
�@�������C(4)��
�@���Ƃ��C�_ �ƂȂ邪�C(3)�ōl���Ă݂�ƕ�����悤�� ��\���Ă���D���ꂪ�O�ɂȂ�Ȃ��������ł� ��\���D �@�܂��C���Ƃ��C�_ �ƂȂ邪�C(3)�ōl���Ă݂�ƕ�����悤�� ��\���Ă���D���ꂪ�O�ɂȂ�Ȃ��������ł� ��\���D�Ȃ��C�������Ȃ����Ƃ͕������Ƃ��ď����Ȃ��Ă悢����C����͎��̌`�ɏ�����D �@
�y�v�_�z
�Z�@3������Ԃɂ����āC�Q�_ (2)�`(4)�����l |
|
���̓_��ʂ钼���̃p�����[�^�����������߂�D
1.(1, 1, −1)��(−2, 1, 3)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.15
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
1.A(1, 1, −1),B(−2, 1, 3)�Ƃ����ƁC�_A��ʂ�C�����x�N�g��
�ɕ��s�Ȓ��������� �����ɕ����āC���̌`�ŏ����Ă��悢�D B(−2, 1, 3)��ʂ�C�����x�N�g�� �ɕ��s�Ȓ����ƍl����� �����ɕ����āC���̌`�ŏ����Ă��悢�D �i�Q�l1�j���̒����̕��������Cxyz�̕������ŏ����� �i�Q�l2�j�a����p���ł́C�R������Ԃ̓_�̍��W���x�N�g�����C������� �ƂȂ��Ă���D �@������������̂����C �@�Ȃ��C(��3)�̃p�����[�^�� �i �ƂȂ��āC���������قȂ邪�C�\���Ă�����͓̂��� |
���̓_��ʂ钼���̃p�����[�^�����������߂�D
2.(−1, 5, 2)��(3, −4, 1)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.15
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
1.A(−1, 5, 2),B(3, −4, 1)�Ƃ����ƁC�_A��ʂ�C�����x�N�g��
�ɕ��s�Ȓ��������� �����ɕ����āC���̌`�ŏ����Ă��悢�D �i�Q�l�j�a����p���ł́C�� |
|
** �Q�������ʂɂ����钼���̕����� **
�y�v�_�z
�i����j���ʏ�łP�_��ʂ�C�^����ꂽ�x�N�g���ɐ����Ȓ����̕�����
�Z���ʂɂ����āC�_
�Z���ʂɂ����āC�_ 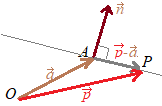 �_
�_
�����藧�D���������� �����藧�D�܂��C�t��(2)�����藧�ĂC�_ |
���̂`�Ƃo�ɑ��āA�o��ʂ�`�ɐ����ȁi�Q-��Ԃ́j�����̕����������߂�D
��1 ��L�̋��ȏ��ł́C�_�̍��W���x�N�g�����C�������
3.A=(1, −1)�CP=(−5, 3)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.15
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037 ��2 ��L�̋��ȏ��ł́C�Q�����̕��� R2�̂��Ƃ�(�Q-��ԁj�C�R�����̋�� R3�̂��Ƃ��i�R-��ԁj�Ə����Ă���D
���̂`�Ƃo�ɑ��āA�o��ʂ�`�ɐ����ȁi�Q-��Ԃ́j�����̕����������߂�D
��1 ��2 ����
4.A=(−5, 4)�CP=(3, 2)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.15
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037 |
|
** �Q�������ʂɂ�����Q�����̕��s�����C�������� **
�y�v�_�z
���ʏ�̂Q�����̕��s�����C��������
�Z���ʏ�̂Q�����̖@���x�N�g�� �����s�ł���Ƃ��C�Q�����͕��s�ɂȂ�D �Z���ʏ�̂Q���� �̖@���x�N�g�� �������ł���Ƃ��C�Q�����͐����ɂȂ�D |
�i����j �}��`���C���炩 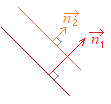 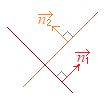 |
|
5.�Q����3x−5y=1, 2x+3y=5�͐����łȂ����Ƃ������D
��1 ��2 ����
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.15
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
�萔��1, 5�͌��ʂɉe�����Ȃ��D
�e�X�̖@���x�N�g���� ���i�Q�l�j ���{�̒��w�Z�C���Z�ŏK��2�����̐��������͎��̌`�ɂȂ��Ă���D
y=m1x+k1…�@
������g���Ď�����y=m2x+k2…�A �ɂ��ć@�ۇA←→m1m2=−1 �̌X���́C�e�X ���̂Ƃ� �ł��邩��C�����̂Q�����͐����łȂ�…�i�ؖ��I�j |
6.���̒����̑g�̂����C�����Ȃ̂͂ǂꂩ�D
(a)�@3x−5y=1��2x+y=2
(b)�@2x+7y=1��x−y=5 (c)�@3x−5y=1��5x+3y=7 (d)�@−x+y=2��x+y=9
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
�萔���͌��ʂɉe�����Ȃ��D
(a) �e�X�̖@���x�N�g���� (b) �e�X�̖@���x�N�g���� (c) �e�X�̖@���x�N�g���� (d) �e�X�̖@���x�N�g���� �ȏ�ɂ��C(c)(d)…�i���j ���i�Q�l�j ���{�̒��w�Z�C���Z�ŏK��2�����̐�������
y=m1x+k1…�@
���g����y=m2x+k2…�A �ɂ��ć@�ۇA←→m1m2=−1 (a) (b) (c) (d) �ȏ�ɂ��C(c)(d)…�i���j |
|
** �R������Ԃɂ����镽�ʂ̕����� **
�y�v�_�z
�i����j1�_��ʂ�^����ꂽ�@���x�N�g���ɐ����ȕ��ʂ̕�����
�Z�i�R������Ԃɂ����āj�_
�Z�i�R������Ԃɂ����āj�_ 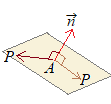 �_
�_
������ �����藧�D�t��������D ����𐬕��ŏ����� |
7.���̓_�o��ʂ�C�x�N�g���m�ɐ����ȕ��ʂ̕����������߂�D
(a)�@N=(1, −1, 3)P=(4, 2, −1) (b)�@N=(−3, −2, 4)P=(2, ��, −5) (c)�@N=(−1, 0, 5)P=(2, 3, 7)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
(a)�@1·(x−4)−1·(y−2)+3·(z+1)=0
x−y+3z+1=0…�i���j (b)�@−3·(x−2)−2·(y−��)+4·(z+5)=0 −3x−2y+4z+2��+26=0…�i���j (c)�@−1·(x−2)+0·(y−3)+5·(z−7)=0 −x+5z−33=0…�i���j |
|
�y�v�_�z
�i����j�R�_��ʂ镽�ʂ̕�����
�Z �i�R������Ԃɂ����āj�R�_�Ƃ����āC 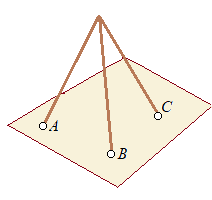 �@�R�_���꒼����ɕ���ł���ꍇ�������C�ʏ�C�R�_��ʂ镽�ʂ͂����P�ʂ�ɒ�܂�D
�@�R�_���꒼����ɕ���ł���ꍇ�������C�ʏ�C�R�_��ʂ镽�ʂ͂����P�ʂ�ɒ�܂�D�@���Ȃ̎������⑪�ʊ��ȂǁC���������v���������͂R�{���ɂȂ��Ă���̂́C�R�_�ɂ���ƕ��ʂ��m�肷��Ƃ������Ƃ𗘗p�������̂ł���D
8.���̂R�_��ʂ镽�ʂ̕����������߂�D
�i�j(a)�@(2, 1, 1), (3, −1, 1), (4, 1, −1)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037 �@���߂镽�ʂ̕������� �Ƃ����D �_(2, 1, 1)��ʂ邩�� �_(3, −1, 1)��ʂ邩�� �_(4, 1, −1)��ʂ邩�� |
�@�������̌��i�R�j�����m��
�́C�m�肵�������������C�s��������D
����́C���̂ǂ̕��������������̂�\���Ƃ������ƂƑΉ����Ă���D
�A��������(1)(2)(3)�������Ƃ��ɁC������h�����߂ɂ́C�P�̕����C�Ⴆ��
���̂悤�ɁC���߂�������� ���̂悤�ɂ���ƁC���m����3�C��������3�̘A���������ƂȂ�C���Z�ʼn������ꂽ�`�ɂȂ�D �@�܂��C(1)−(2), (2)+(3)�ɂ�� (5)��� (4)�ɑ�� (1)�ɑ�� �ȏォ�� ���ӂ�
��
�Ȃǂ��C���������ɂȂ邪�C�ʏ�͂Ȃ�ׂ��ȒP�Ȑ����䂪�D�܂�邩��C��L�́i���j���悢�D |
|
(�Q�l1�j �@�t�s��̋��ߕ����K���Ă���ꍇ�C��L�̘A�������������̂悤�ɉ����ƌ��ʂ����悢 �́C�s���p���Ď��̌`�ɏ�����D ���ӂɍ�����W���s��̋t�s����|����� (�Q�l2�j �@�N�����[���̌������K���Ă���ꍇ�C��L�̘A���������͎��̂悤�ɉ����� |
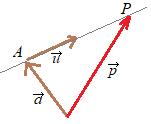 (�Q�l3�j
(�Q�l3�j�Z�_ �ŕ\�����D������C���� �����ď����� (3)������}��ϐ� (1)�͔C�ӂ̒l���Ƃ�ϐ����P���邩��C���R�x�P���Ȃ킿1������ԁC������\���D 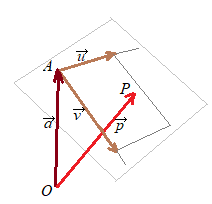 �Z�_
�Z�_
�ŕ\�����D������C���� ��p���ĕ\���� �����ď����� ����炩��C�܂��}��ϐ� (1’)�͔C�ӂ̒l���Ƃ�ϐ����Q���邩��C���R�x�Q���Ȃ킿�Q������ԁC���ʂ�\���D 8.(a)�̖����C�_A(2, 1, 1)��ʂ�x�N�g�� �����ď����� (3’)����}��ϐ� �ƂȂ��āC�O�q�Ɠ������ʂ�D |
|
8.���̂R�_��ʂ镽�ʂ̕����������߂�D
(b)�@(−2, 3, −1), (2, 2, 3), (−4, −1, 1)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
�@���߂镽�ʂ̕�������
�Ƃ����D ���̘A���������������� ���������āC���ʂ̕������� ���Ȃ킿 |
8.���̂R�_��ʂ镽�ʂ̕����������߂�D
(c)�@(−5, −1, 2), (1, 2, −1), (3, −1, 2)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.037
�@���߂镽�ʂ̕�������
�Ƃ����D ���̘A���������������� ���������āC���ʂ̕������� ���Ȃ킿 |
|
**�R������Ԃɂ����ĂQ�̃x�N�g���ɐ����ȃx�N�g��**
9.(1, 2, −3)�����(2, −1, 3)�ɐ����ȃx�N�g�������߂�D
�i��1�j
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.038 �@
�@���̘A��������(1)(2)�������āC�x�N�g��
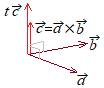 �@���̂��߁C���̕������͎��R�x�P�̕s����i�C�ӂ̒l���Ƃ�}��ϐ����P�܂މ��j�ɂȂ�D
�@���̂��߁C���̕������͎��R�x�P�̕s����i�C�ӂ̒l���Ƃ�}��ϐ����P�܂މ��j�ɂȂ�D�@����́C�E�}�̂悤�ɂ���x�N�g�� �@���ۂɉ����Ƃ��́C�}��ϐ��ɑI�ԕϐ����P�I�сC���̕����ő��̕�����\���Ƃ悢�D (1’)+(2’)�~2 �����(2’)�̑�� �ȏォ�� �i��1’�j←���R�C���̌`�ł��悢�D �i��2�j←���Z�ł́C��x�N�g�� �i��3�j←��w�ł́C��x�N�g���͔C�ӂ̃x�N�g���ɐ����ƒ�`���邩��C��L�̏��� |
�i��2�j �t�s���p���ĘA���������������ꍇ ��� ���ӂɍ�����W���s��̋t�s����|����� �ȉ��̓��ẮC�i��1�j�Ɠ��l �i��3�j �N�����[���̌�����p���ĘA���������������ꍇ �̉��́i�W���s��̍s���O�łȂ��Ƃ��j �̉��� �ȉ��̓��ẮC�i��1�j�Ɠ��l �i��4�j 
�Q�̃x�N�g��
|
|
** �R������Ԃɂ�����Q���ʂ̌�� **
�y�v�_�z
�Z�i�R������Ԃɂ����āj�_ ���̕������𐬕� �����ɕ������ (3)������}��ϐ� ����(4)���́C�A�������� �ƌ��邱�Ƃ��ł���D (5)�����(6)�͊e�X���ʂ̕�����������C��Ԃɂ����钼���̕������́C�Q���ʂ̌���Ƃ��ĕ\����Ă��邱�ƂɂȂ�D �Z�i�R������Ԃɂ����āj�Q���� 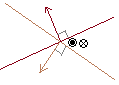 �Q�̕��ʂɐ����Ȓf�ʂ��猩���} �Q�̕��ʂɐ����Ȓf�ʂ��猩���}�L�� |
14.�Q����2x−y+z=1 , 3x+y+z=2�̌���̃p�����[�^�����������߂�D(���12.�Ή���)
�i��1�j
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.038 �A�������� �̉������߂�D�������̌����Q�ŁC���m���̌��R�����P���Ȃ�����C�}��ϐ����P�܂s����ɂȂ�D�����ŁC�P�����ɂ��Ă͉����Ȃ��ƌ��߂�D�i (1)+(2)���
�a����p���̉́C
�����(1)�ɑ���Ƃ���ΑΉ����� �}��ϐ��� �}��ϐ��� �܂��� |
|
�i��2�j �@3������Ԃɂ����钼���̕������́C�ʂ�ׂ��P�_ �@2x−y+z=1 , 3x+y+z=2�ɂ����āCy=0�̂Ƃ���x=1, z=−1�ƂȂ邩��C�_ �@���߂钼���̕����x�N�g�� ����������� ���������� �P�̕����x�N�g���� |
�i��3�j �@3������Ԃɂ����钼���̕������́C�ʂ�ׂ��P�_ �i��2�j�ɂ����āC�ʂ�ׂ��P�_�̍��W�����߂�ꂽ����l���Ă݂�ƁC�A�������� �́C���m����3�ł���̂ɑ��āC��������2�Ə��Ȃ����߁C���̂܂܂ł͕s����ƂȂ�Ƃ�����C�P�����lj����āiy�ɓ���̒l�������āC�萔�ɂ��āj���m���̌���2�ɂ���C����̓_�̍��W����܂邱�Ƃ𗘗p�����D��̓I�ɂ́Cy=0�Ƃ����x=1, z=−1�ƂȂ邱�Ƃ���C�_ �@���̍�Ƃ�����1��s���C2�ڂ̓_���������2�_�`�C�a��������C�_�`��ʂ�x�N�g�� �@x=0�Ƃ���� �@���̂Ƃ��C |
|
14.(����)�Q����2x+y+5z=2 , 3x−2y+z=3�̌���̃p�����[�^�����������߂�D(���13.�Ή���)
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.038
�i��1�j
�A�������� �̉������߂�D�������̌����Q�ŁC���m���̌��R�����P���Ȃ�����C�}��ϐ����P�܂s����ɂȂ�D�����ŁC�P�����ɂ��Ă͉����Ȃ��ƌ��߂�D�i �}��ϐ��� �}��ϐ��� �܂��� |
�O��Ɠ��l�Ɂi��2�j�i��3�j�̂悤�ɉ����Ă��悢�D�����ł́i��3�j�������D z=0�Ƃ����x=1, y=0�ƂȂ邩��C�_A(1, 0, 0)��ʂ�D �܂��Cx=0�Ƃ���� �����ŁC�_A(1, 0, 0)��ʂ�C�����x�N�g�� �����x�N�g���Ƃ��� |
** �R������Ԃɂ����ĂQ���ʂ��Ȃ��p **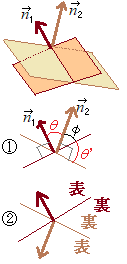 �y�v�_�z
�y�v�_�z�Z�i�R������Ԃɂ����āj2���ʂ��Ȃ��p�́C�����̖@���x�N�g�����Ȃ��p�ɓ������D
(��)�E�}�@�̂悤�Ȓf�ʂ��猩���ꍇ�C
�������C�A�̂悤�ɖ@���x�N�g���̌����ɂ���ẮC90��<�Ɓ�180���ɂȂ��Ă��܂��ꍇ������D��+��=90�� ��’+��=90�� ������ ��=��’ �����藧�� �@���Z�ł́C2���ʂ̂Ȃ��p�́C0�����Ɓ�90����90��<�Ɓ�180���̂Q���邤���̏��������C0�����Ɓ�90���œ�����̂����ʂł���D �i�������O�{�̘a��ł́C�@���x�N�g�����Ȃ��p���̂܂ܕ��C�œ�����悤�ɂȂ��Ă���j ������ �������C���Z�ł� |
15.���̂Q���ʂ̂Ȃ��p�̗]�������߂�
(a)�@x+y+z=1 , x−y−z=5
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.039 |
|
15.���̂Q���ʂ̂Ȃ��p�̗]�������߂�
(c)�@x+2y−z=1 , −x+3y+z=2
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.039 |
16.���̂Q���ʂ̂Ȃ��p�̗]�������߂�
(d)�@2x+y+z=3 , −x−y+z=��
�i���p���jSerge Lang�uLINEAR ALGEBRA�v1��5,P.16
�i�a����p���j�����O�u���`�㐔�w(��)�v1�́�5, P.039 |