■Rを用いた固有値・固有ベクトルの計算

○この頁の内容

　右の表１のように成分が数値で与えられた正方行列の固有値と固有ベクトルを統計解析用のフリーソフトRで計算する方法の解説
表１
6 4 2
5 7 4
-5 -5 0
○固有値，固有ベクトルとは（簡単な復習）
　
与えられた正方行列Aに対して
A=λ (≠) …(1)
を満たすλとが存在するとき，λを行列Aの固有値といい，をλに属する（対する）固有ベクトルという．
○　一般にｎ次正方行列に対する固有方程式はｎ次方程式になり，ｎ次方程式の解は（重解や虚数解も含めると）ｎ個存在する…２次の正方行列の固有値は２個，３次の正方行列の固有値は３個，…である．


※固有ベクトルの大きさは決まらない．（あるベクトルが固有ベクトルであればその定数倍（≠0倍）もすべて固有ベクトルになる．Rで固有ベクトルを求めたときは，この頁の末尾で示すように単位ベクトル（方向を変えずに大きさを１にしたベクトル）で示される．）		 例えば，表1の行列を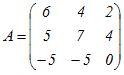とおくとき，
固有値λ1=6，固有ベクトル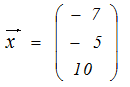に対して， A=λ1 が成り立つ．
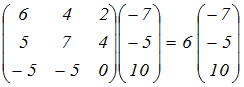　この行列Aは３次正方行列であるから，この他に２つの固有値があり，合計３個の固有値とそれぞれに対応する固有ベクトルが存在する．
　これら３組をRで求めるにはどうすればよいかというのがこの頁の内容
○処理の流れ

(1)Excelの起動→(2)Rの起動→(3)Rコマンダーの起動
→(4)データのインポート
→(5)Rコンソールにコマンドを入力する
→(6)固有値・固有ベクトルを出力する
→Rコマンダーの終了→Rの終了→Excelの終了
 ※　ＲとＲコマンダー（RExcel）のインストール方法についてはこの頁参照

※　他の処理と共通な(1)〜(3)および終了処理についてはここでは省略して左の(4)〜(6)のみを解説する．
(4)データのインポート
i)　クリップボード（メモリ）経由のとき
　右ようなWeb画面上のテーブルから取り込む（インポートする）ときは，画面上で左上（x1の左）から右下（0の右）までをドラッグしてコピーし，これを単純にExcelに貼り付けるとよい．（Web画面をそのままインポートするとうまくいかない）
　次に（もしくは初めからデータがExcel上にあるとき）Excel画面でもう一度コピーしてクリップボードに入れる．
　Rコマンダーのメニューから
データ→データのインポート→テキストまたはクリップボード，URLから→
データセット名：そのまま（Dataset）
ファイル内に変数名あり：右の解説参照
データファイルの場所：クリップボード
フィールドの区切り記号：「タブ」にチェック
→OK
（「データセットを表示」で確認しておくとよい．）
ii)　Excelファイルからインポートするとき

　Rコマンダーのメニューから
データ→データのインポート→Excel，AccessまたはdBaseのデータセットから→
データセット名：短い名前にするとき（Dなど）
→OK
→フォルダー，ファイルの選択
→Sheetの選択
→OK
（「データセットを表示」で確認しておくとよい．）
x1 x2 x3
6 4 2
5 7 4
-5 -5 0
　（A)　Excel上のデータで右図の変数名(x1〜x3)を含めてコピーした場合には「ファイル内に変数名あり」にチェックを入れる（=デフォルト）．
　（B)　Excel上のデータで右図の変数名(x1〜x3)を含めずに黄色で示したデータ部分だけをコピーした場合には「ファイル内に変数名あり」のチェックを外す．






ii）　の場合は，右図（Ａ）の方法で列ラベル=変数名をセットしておくことが重要．これがないと１行目がデータラベルに取り込まれて，正方行列ではなくなる．
.
(5)Rコンソールにコマンドを入力する
Excel以外にウインドウが３個または４個開いている状態になっているので，そのうちの「R　console」ウインドウに右のコマンドを入力する．
（入力ミスを防ぐにはコピー・貼り付けするとよい．末尾のEnterがコピーできなかったときはキーボードからEnterを入力するとよい．）
データセットDatasetの固有値と固有ベクトルを求めて，データセットｙに代入する．
y<-eigen(Dataset)
(6)固有値・固有ベクトルを出力する
　データセット　ｙ　の中身を表示すればよい．
y
※Rでのデータセット名としてDataset以外の名前にしているときは，Datasetをその名前に書き換える：たとえばy<-eigen(D)

※例えば　y<-eigen(D)　によってデータセットDの固有値・固有ベクトルを求めたものがｙというデータセットに入力されるので，
２つ目のコマンド　ｙ　によってその中身である固有値と固有ベクトルが表示される．
○表示されるもの
　右のように表示されたとき，$valueが固有値を表す．
（固有値だけを表示したいときは，y$valueと入力する．）
　$vectorsの列ベクトルが各固有値に対応する固有ベクトルを表す．（右の３列目はExcelの場合と同様に非常に小さな数の場合において指数表示になっている．）

　固有べクトルは規格化（大きさを１にすること）されているので，例えば固有値6に対する固有ベクトルが整数値で表されるベクトル ｔ(7,5,-10) に対応していることに気づくのは難しいかもしれない．
　同様にして右の例では固有値5に対する固有ベクトルはｔ(2,1,-3) ，固有値2に対する固有ベクトルはｔ(-1,1,0) になっている．		 > y
$values
[1] 6 5 2

$vectors
[,1] [,2] [,3]
[1,] 0.5306686 -0.5345225 -7.071068e-01
[2,] 0.3790490 -0.2672612 7.071068e-01
[3,] -0.7580980 0.8017837 1.950852e-16
■練習問題■
　次の各正方行列について固有値と固有ベクトルを求めよ．
(1)
-3 -2 -1
0 1 2
3 4 5
$values
[1] 6.000000e+00 -3.000000e+00 -4.018708e-17
⇒固有値 6, -3, 0
$vectors
[,1] [,2] [,3]
[1,] -0.1825742 0.8728716 0.4082483
[2,] 0.3651484 0.2182179 -0.8164966
[3,] 0.9128709 -0.4364358 0.4082483
⇒この固有ベクトルは，整数値では
　ｔ(-1,2,5) , ｔ(4,1,-2) ,ｔ(1,-2,1) に対応している．
(2)
0 2 -2 1
-3 5 1 -2
-2 1 0 2
1 -2 -3 5
$values
[1] 6.000000e+00 3.000000e+00 1.000000e+00 1.328004e-15
⇒固有値 6, 3, 1, 0
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.1714986 -0.5 0.5 0.5883484
[2,] -0.6859943 -0.5 0.5 0.3922323
[3,] 0.1714986 0.5 0.5 0.5883484
[4,] 0.6859943 0.5 0.5 0.3922323
⇒この固有ベクトルは，整数値では
　ｔ(-1,-4,1,4) , ｔ(-1,-1,1,1) ,ｔ(1,1,1,1) ,ｔ(3,2,3,2)に対応している．
固有値や固有ベクトルが虚数となる場合でも求めることができる．
(3)
3 2
-2 3
$values
[1] 3+2i 3-2i

$vectors
[,1] [,2]
[1,] 0.7071068+0.0000000i 0.7071068+0.0000000i
[2,] 0.0000000+0.7071068i 0.0000000-0.7071068i
⇒この固有ベクトルは，整数係数では
　ｔ(1,i) , ｔ(1, -i)に対応している．
...メニューに戻る　..Rのメニューに戻る