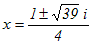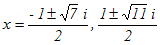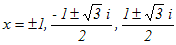■５次方程式の解

○　はじめに

５次方程式
ax5+bx4+cx3+dx2+ex+f=0 (a≠0) …(1)
を代数的に解くことはできない．（アーベル）」

　上の有名な定理は，実際に数値で係数が与えられたときに「５次方程式が解けない」ことを意味しているのではない．例えば，次の５次方程式は解ける．
x5−5x4+8x3+32x2−153x+117=0 …(2)

　例えば，初めは適当な値（右図では−0.5の値）から接線を引いてｘ軸と交わる点を求める．そのｘ座標に対応する曲線上の点から再び接線を引いてｘ軸と交わる点を求める．（右図において赤で示したのが曲線上の点）
　このような手順を何度も繰り返すと右図のx=1が得られる．［ニュートン法と呼ばれる．］
　もとが５次方程式なら，x−1で割ることにより４次方程式に変わり，残りの解も求められる．

※「５次方程式の解の公式がない」とは，有限回の加減乗除の四則計算と累乗根を求める計算だけを使って」解を求めることはできないということで，コンピュータを使って何度も　（これを無限回と見なせばよい）　近似を繰り返していくと，数値解は求まる．
【要点】
　「５次方程式の解の公式はない」が，コンピュータを使えば「数値係数の５次方程式の解は求められる」．
（*）代数的にとは，「有限回の加減乗除の四則計算と累乗根を求める計算だけを使って」ということ．


(2)式は (x−1)(x2−4x+13)(x2−9)=0 と変形できるので，この方程式の解は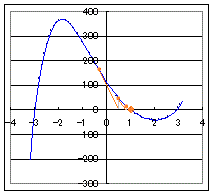
x=1, 2±3i, ±3
となる．

○　Ｒコマンダーを用いた５次方程式の解き方

　ＲのconsoleウィンドウまたはＲコマンダーのスクリプトウィンドウに次の水色文字の部分をコピーして貼り付ける．
polyroot(c(113,-149,32,8,-5,1))
この後
⇒Ｒのconsoleウィンドウに貼り付けているときは，Enterキーを押す．
⇒Ｒコマンダーのスクリプトウィンドウに貼り付けているときは，マウスをその行にポイントしておいて［実行］ボタンをクリックする．
［結果］
ＲのconsoleウィンドウまたはＲコマンダーの出力ウィンドウに次の結果が出力される．
polyroot(c(113,-149,32,8,-5,1))
[1]  1.000000+0.000000i -2.980212+0.000000i 2.931663-0.000000i
[4]  2.024275-2.972515i  2.024275+2.972515i
これらは，方程式の解がx=1, −3, 3, 2−3i, 2+3iであることを表している． 		polyroot()は多項式の値が0となるｘの値（要するに多項式型の方程式の解）を求める関数

引数には，c()という順序を付けて数値を代入する関数（ベクトルに成分を代入する関数）に方程式の係数を昇順に（次数の低い方から）カンマで区切って代入する．
例
x2−4x+3=0 → polyroot(c(3,-4,1))
5x3+3x2−2x−3=0 → polyroot(c(-3,-2,3,5))








※近似解になるので注意

○　２次〜６次方程式の例
　各々(1)方程式　，(2)因数分解→解，(3)ＲのconsoleウィンドウまたはＲコマンダーのスクリプトウィンドウに入力する文字，(4)結果として出力されるもの　の順
【２次方程式】
(1) x2−2x−8=0 (2) (x+2)(x−4)=0 → x=−2 , 4
(3) polyroot(c(-8,-2,1))
(4) -2+0i 4-0i

(1) 6x2−7x−20=0 (2) (3x+4)(2x−5)=0 → x=− ,
(3) polyroot(c(-20,-7,6))
(4) -1.333333-0i 2.500000+0i

(1) 2x2−x+5=0 (2) 因数分解できないので解の公式で解く →
(3) polyroot(c(5,-1,2))
(4) 0.25+1.561249i 0.25-1.561249i
【3次方程式】
(1) x3+3x2−6x−8=0 (2) (x+1)(x−2)(x+4)=0 → x=−1 , 2, −4
(3) polyroot(c(-8,-6,3,1))
(4) -1-0i 2-0i -4+0i
【4次方程式】
(1) x4+4x2+x+6=0 (2) (x2+x+2)(x2−x+3)=0 →
(3) polyroot(c(6,1,4,0,1))
(4) 0.5+1.658312i -0.5+1.322876i -0.5-1.322876i 0.5-1.658312i

【5次方程式】
(1) x5+x4−15x3−x2+38x−24=0
(2) (x−1)(x+2)(x−3)(x+4)=0 → x=1(重解), −2, 3, −4
(3) polyroot(c(-24,38,-1,-15,1,1))
(4) 1+0i 1-0i -2+0i 3-0i -4-0i

【6次方程式】
(1) x6−1=0
(2) (x−1)(x+1)(x2+x+1)(x2−x+1)=0 →
(3) polyroot(c(-1,0,0,0,0,0,1))
(4) 0.5+0.8660254i -0.5+0.8660254i -0.5-0.8660254i 1.0+0.0000000i -1.0-0.0000000i 0.5-0.8660254i

　上の例では結果が分かりやすいように整数係数の問題ばかりを選んだが，理科で用いられるような小数係数の方程式も解ける．
【問題】　次の方程式を解け．
(1) x7=−1
(2) 1.1x6−2.1x5+3.1x3−1=0
(3) 1903x5+2011x3−41x+97=0
 【解答】
(1) x7+1=0と変形し，polyroot(c(1,0,0,0,0,0,0,1))を用いる．
結果：0.9009689+0.4338837i ，-0.6234898+0.7818315i ，
-0.6234898-0.7818315i ，0.9009689-0.4338837i ，
0.2225209+0.9749279i ，-1.0000000+0.0000000i ，
0.2225209-0.9749279i
（解は7個あり -1以外は虚数解）

(2) polyroot(c(-1,0,0,3.1,-2.1,1.1))を用いる．
結果：0.7769173-0.0000000i -0.3782052+0.5004629i
-0.3782052-0.5004629i 0.9442920-1.4428899i
0.9442920+1.4428899i

(2) polyroot(c(97, -41, 0,2011, 0, 1903))を用いる．
結果：0.2048872+0.2942538i ，　-0.3669701-0.0000000i
0.2048872-0.2942538i ， -0.0214021-1.0392004i
-0.0214021+1.0392004i
...メニューに戻る　..Rのメニューに戻る