|
【公式】
(解説1)点(a, b)を通り傾きmの直線の方程式は y−b=m(x−a) で表わされます. 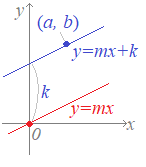 原点を通り,傾きがmの直線の方程式はy=mxですが,
原点を通り,傾きがmの直線の方程式はy=mxですが,必ずしも原点でない点(a, b)を通っている場合には,y切片kの値(定数)を求めておく必要があります. y=mx+k…(1)が点(a, b)を通るということからkの値が定まります. x=a, y=bを(1)に代入すると成り立つはずだから
y軸との交点のy座標を中学校では「切片」と言いますが,高校ではy切片と言います.
b=ma+kx軸との交点「x切片」と区別するためです. したがって k=b−ma…(2) (2)を(1)に代入すると y=mx+(b−ma)…(3) この形は,あまり覚えやす形でないので,次の形に直して公式にします. y−b=m(x−a)…(公式) |
(解説2) 既知の定数を青で示し,未知の定数を赤で示す.x, yは変数 y=mx+k b=ma+k 辺々引くと,未知の定数を使わずに,x, yの間に成り立つ関係が書ける. y−b=m(x−a)…(公式)
【少しでも印象に残しておこう】
(1) 「足す」のでなく「引く」 y−b=m(x−a)…(公式) (2) y座標はyと組む,x座標はxと組む |
