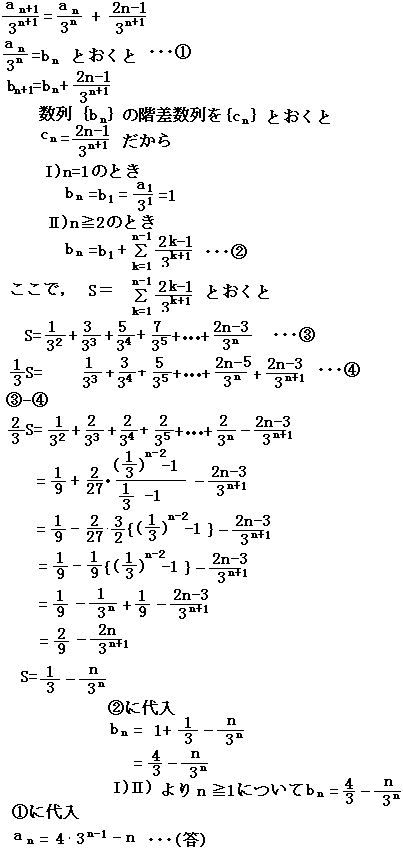
an+1+n+1=3(an+n)と変形すると数列{an+n}は公比3の等比数列になるから
an+n=(a1+1)3n-1
=4・3n-1
an==4・3n-1-n・・・(答)
|
________ |
が,お勧め答案.他は参考. |
| △階差数列に持ち込む方法
「an+1=2an+1 (n≧1)・・・(1) an=2an-1+1 (n≧2)・・・(2) (1)-(2) an+1-an=2(an-an-1) (n≧2)・・・(3) 数列{an+1-an}は公比2の等比数列数列{an}の階差数列が bn=an+1-an =2n だから ア) n≧2のとき an=a1+Σn-1k=12k =1+2(2n-1-1) =1+2n-2 =2n-1 イ) n=1のとき a1=1 ア)イ)よりan=2n-1 (n≧1)・・・(答)」 |
|
◇推定+数学的帰納法による方法
「a1=1 a2=2+1 a3=2(2+1)+1=22+2+1 a4=2(22+2+1)+1=23+22+2+1 ・・・ an=2n-1+・・・+22+2+1 =2n-1と推定する. これを数学的帰納法により証明する:以上より,an=2n-1 ・・・(答)」 |
| ○階差数列に持ち込む方法
「an+1=an+2 (n≧1)・・・(1) 数列{an}の階差数列が (別解) 「(1)より 数列{an}は公差2の等差数列 だから an=1+(n-1)・2=2n-1・・・(答)」 |
|
◇推定+数学的帰納法による方法
「a1=1 a2=2+1 a3=2+2+1 a4=2+2+2+1 ・・・ an=2+・・・+2+2+1 =2(n-1)+1=2n-1と推定する. これを数学的帰納法により証明する:以上より,an=2n-1 ・・・(答)」 |
△通常この解法で説明しますが,(2)以降の計算が長くなるのが難点です.
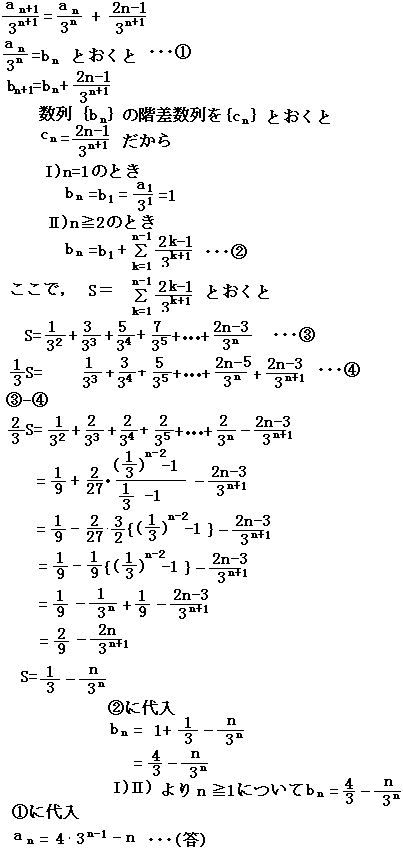 |
○等比数列にする方法
an+1+n+1=3(an+n)と変形すると数列{an+n}は公比3の等比数列になるから
|
△通常の解法
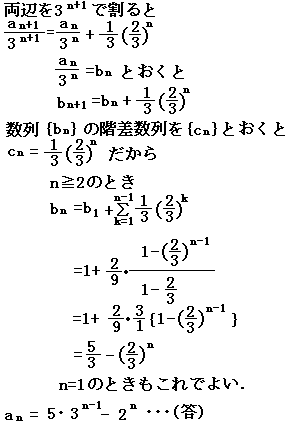 |
○等比数列にする方法
an+1+2n+1=3(an+2n)と変形すると,数列{an+2n}は公比3の等比数列になるから an+2n=(a1+21)3n-1=5・3n-1 an=5・3n-1-2n・・・(答) |
○等比数列にする方法
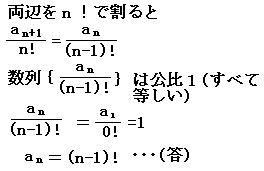 |
◇推定+数学的帰納法による方法
a1=1 a2=1・1 a3=2・1・1 a4=3・2・1・1 a5=4・3・2・1・1 ・・・ an=(n-1)! と推定する. これを数学的帰納法で証明する.an=(n-1)!・・・(答) |
○等比数列にする方法
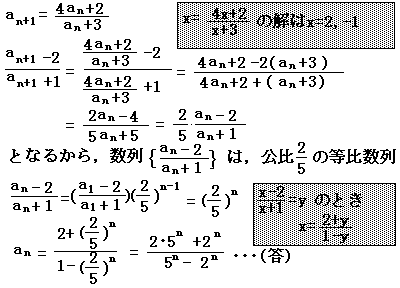 |
○等比数列にする方法
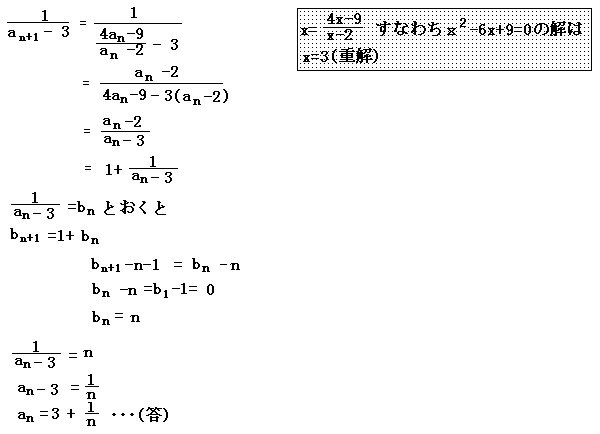 |
○等比数列にする方法
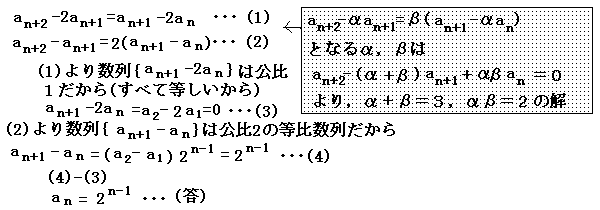 |
○等比数列にする方法
|