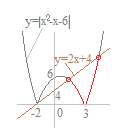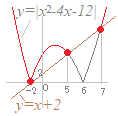|
〇絶対値付きの2次不等式を解くには,場合分けによって絶対値記号を外してから解くのが確実です.
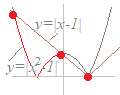
【例1】
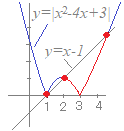
(解答)2次不等式x2−2|x|−3≦0を解いてください.
絶対値記号は,絶対値の中に収められている文字式の符号に応じて外すことができます.
ア) x≧0のとき
分かれば簡単なことのようですが,次のような間違い答案が結構多い.こんな答案を書かれたら,採点官の「はらわたが煮えくり返って」完全な0点にしたくなる.
※|x|はつねに正または0だから,こんな場合分けはありえない.何も分かっていない生徒の答案に見える## x2−2x−3≦0を解く 2次方程式 x2−2x−3=0 (x+1)(x−3)=0 の解は x=−1 , 3 だから 2次不等式の解は −1≦x≦3…(*) ア)と(*)の共通部分から, 0≦x≦3 イ) x<0のとき x2+2x−3≦0を解く 2次方程式 x2+2x−3=0 (x−1)(x+3)=0 の解は x=1 , −3 だから 2次不等式の解は −3≦x≦1…(**) イ)と(**)の共通部分から, −3≦x≦0 ア)イ)より −3≦x≦3…(答) |
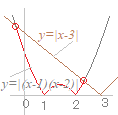
【例2】
(解答)2次不等式x2−3|x−1|−1>0を解いてください.
絶対値記号は,絶対値の中身全体の符号に応じて外します.
ア) x≧1のとき次の式で,中身全体とはx−1のことです.
ただし,紺色で書いた場合分けは,xの値としては間接的過ぎますので,もっと直接的に次のように書きます.
次のような間違い答案も結構多い.こんな答案を書かれたら,採点官の「はらわたが煮えくり返って」完全な0点にしたくなる.
※|x|のはずし方の公式を丸暗記して書いただけで,何も分かっていない生徒の答案に見える## x2−3(x−1)−1>0 x2−3x+2>0 2次方程式 x2−3x+2=0 (x−1)(x−2)=0 の解は x=1 , 2 だから 2次不等式の解は x<1 , 2<x…(*) ア)と(*)の共通部分から, 2<x イ) x<1のとき x2+3(x−1)−1>0 x2+3x−4>0 2次方程式 x2+3x−4=0 (x−1)(x+4)=0 の解は x=1 , −4 だから 2次不等式の解は x<−4 , 1<x…(**) イ)と(**)の共通部分から, x<−4 ア)イ)より x<−4 , 2<x…(答) |
 数1では「もれなく」「重複なく」書いてあればOK
数1では「もれなく」「重複なく」書いてあればOK