|
�y�v�_�z
�@3�_ 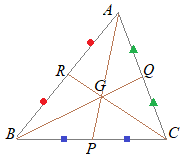 �i�p��j
�i�p��j�O�p�`���`�a�b�̒��_�Ƃ��̑Εӂ̒��_�����Ԓ������C�u�����v�Ƃ����D
���`�a�b�̂R�̒����͂P�_�Ō����D���̓_���u�O�p�`�̏d�S�v�Ƃ����D…(*1)
�i�����Ēʂ�Ȃ�����=�K���[�����Ȃ���Ȃ�Ȃ����Ɓj��L�̒�`(*1)�ɒ����ɏ]���āC�O�p�`�̏d�S�����߂悤�Ƃ���ƁC�u�����̌�_�����߂���@�v��������Ȃ���Ȃ�܂��C���Z���w�̋��ނ̕��ו����猾���ƁC�d�S�̍��W���K���i�K�ł́C�܂��Q�����̌�_�����߂���@���K���Ă��܂���D�i���e�I�ɂ̓x�N�g���������̌�_�m���w�a�n�╡�f�����ʂł̒����̕������u���w�V�v�ŋ��߂邱�Ƃ��ł��܂��j�D �����ŁC���̒i�K�ŏd�S�̍��W�̌������ؖ�����ɂ́C�ʏ�C��L�̏d�S����`(*1)�Əd�S�̒�`���瓱���������(*2)����芷���āC(*2)�������̂��d�S�ɂȂ�Ƃ������Ƃ��g���܂��D
�O�p�`�̏d�S�́C�e�X�̒��_�ƒ��_�����Ԑ�����2�F1�ɓ�������_�ɂȂ��Ă���…(*2)
|
(*2)�̏ؖ�←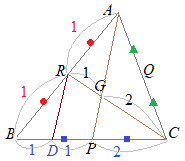 �����̒����́C�����F���m�Łu��v��\�����̂Ƃ��� �܂��C�`�o�Ƃb�q�̌�_���f�Ƃ����ƁC�b�f�F�f�q=2:1�ɂȂ邱�Ƃ������D
�q����`�o�ɕ��s�Ȓ����������C�a�b�Ƃ̌�_���c�Ƃ����ƁC�`�q�F�q�a=1:1������o�c�F�c�a=1:1
���ɁC�a�o=�o�b������ �c�o�F�o�b=1:2 ���������āC�b�f�F�f�q=�b�o�F�o�c=2:1 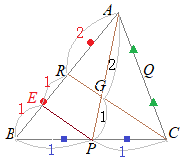
�o����b�q�ɕ��s�Ȓ����������C�`�a�Ƃ̌�_���d�Ƃ����ƁC�b�o�F�o�a=1:1������q�d�F�d�a=1:1
���l�ɂ��āC�����a�p���g���Ăa�f�F�f�p=2:1�ƂȂ邱�Ƃ�������D
���ɁC�a�q=�q�`������ �d�q�F�q�`=1:2 ���������āC�`�f�F�f�o=�`�q�F�q�d=2:1 |