|
|
|
|
|
【予備知識1】
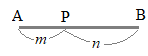 線分ABをm:nに内分する点Pの位置ベクトル
線分ABをm:nに内分する点Pの位置ベクトル※ |
【例】
線分ABを2:3に内分する点Pの位置ベクトル このようにPをA寄りの点にするには(Aに「ひいき」するには)Aに掛ける数字を大きくすることになる |
|
【予備知識2】
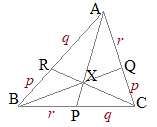 原点をOとし,△ABCの頂点の位置ベクトルを各々
原点をOとし,△ABCの頂点の位置ベクトルを各々によって定まる点Xは (1) と変形すると,ABをq:pに内分する点 をRとおくと,RCをr:(p+q)に内分する点となっている. 同様にして (2) のようにも変形できるから,BCをr:qに内分する点 を,Pとおくと,XはPAをp:(q+r)に内分する点となっている. (3) 内分点Qと線分BQについても同様のことがいえる 逆に,上の図のようにABをq:pに内分する点をRとし,ACをr:pに内分する点をQとするとき,
このとき平面幾何のチェバの定理により
BQ, CRの交点XはBP:PC=r:qになる を満たすこともいえる. |
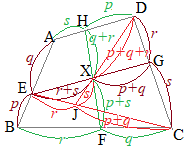 (参考)
(参考)内分点を組み立てていく操作は,何回でも行うことができ,例えば右図のような四角形ABCDについて によって定まる点Xは (1) と変形すれば,右図のEGを(r+s):(p+q)に内分する点となる. (2) と変形すれば,右図のHFを(q+r):(p+s)に内分する点となる. (3) と変形すれば,右図のECをr:(p+q)に内分する点をJとするとき,JDをs:(p+q+r)に内分する点となる. ※(1)(2)(3)は同じ位置ベクトルであるから,同一の点を表す.(上記のように作った線分は1点で交わるともいえる) |
|
【予備知識3】
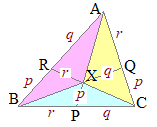 原点をOとし,△ABCの頂点の位置ベクトルを各々
原点をOとし,△ABCの頂点の位置ベクトルを各々△ABCの内部に1点Xをとり,AXの延長が線分BCと交わる点をP,BXの延長が線分CAと交わる点をQ,CXの延長が線分ABと交わる点をRとするとき △XBC:△XCA:△XABの面積比をp:q:rとすると,Xの位置ベクトルは で表される. |
(1) △XBCと△XCAは底辺が共通のXCで,高さの比はその底辺に引いた垂線の長さの比になるが,垂線の長さ自体は図に直接書かれていなくても,XCに交わる線分BR:RAに等しいと言える. 底辺が共通で高さの比が,BR:RAだから,面積の比はBR:RAに等しい. したがって,BR:RA=p:q 同様にして (2) △XBCと△XABは底辺が共通のXBで,高さの比はその底辺に引いた垂線の長さの比になるが,垂線の長さ自体は図に直接書かれていなくても,XBに交わる線分CQ:QAに等しいと言える. 底辺が共通で高さの比が,CQ:QAだから,面積の比はCQ:QAに等しい. したがって,CQ:QA=p:r 同様にして(3)BP:PC=r:qも言える. (1)(2)(3)から定まる点Xは【予備知識2】の図と同じであるから,Xの位置ベクトルは になる. |
|
外心
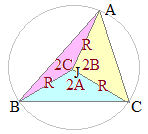 (解説)
(解説)△ABCの外接円の中心(外心)をJとおくと,中学校で習う円周角の定理により,中心角は円周角の2倍になるから,∠BJC=2A, ∠CJA=2B, ∠AJB=2Cとなる. したがって,これらの面積比は 【予備知識3】の結果から |
辺の長さも使って表せば (解説) 2倍角公式によりsin2A=2sinAcosA 正弦定理により B, Cについても同様であるから |
|
■[個別の頁からの質問に対する回答][三角形の重心,内心,外心,垂心(ベクトル,三角関数) について/18.7.12]
勉強になりました。ありがとうございます。
角の2等分線の説明のでは、AB=b AC=c ですが、内心の解説では、AB=c, AC=bとなっており、読んでいて躊躇しました。
また、内心の解説で、BP:PC=AB:AC=b:c と記述があります。図からは、 BP:PC=AB:AC=c:b となります。後者が正しいと思いますがいかがでしょうか。
角の2等分線の説明の記号は、ABCを使わず、UVRとか別な記号を使うといいかもです。
=>[作者]:連絡ありがとう.図の方を直しました. |