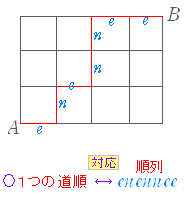
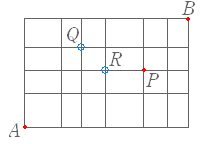
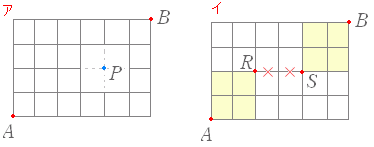
| (1) 下図のような街路があるとき, A 地点から B 地点まで遠回りせずに行く.途中,P 地点も Q 地点も通る道順は何通りあるか. 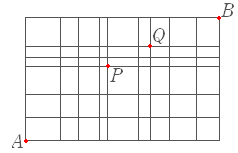 1. 45 通り |
 その各々について P 地点から Q 地点まで:4C2==6 通り その各々について Q 地点から B 地点まで:4C1==4 通り 積の法則により,35×6×4=840 通り(答) ※ 個々の場合を「かつ」で結んで結果が得られるときは,積の法則を用いる. |
| (2) (1)と同じ図で P 地点も Q 地点も通らない道順は何通りあるか. 1. 1197 通り |
P 地点,Q 地点の少なくとも一方を通る道順を求めて全体の道順から引くとよい. P 地点を通る道順 :=1960 Q 地点を通る道順 :=1848 P 地点も Q 地点も通る道順 :・・・(1)より・・・ 840 P 地点,Q 地点の少なくとも一方を通る道順:1960+1848 - 840=2968 P 地点から Q 地点に行く道順は全部で =5005 あるから 5005 - 2968=2037(答) |
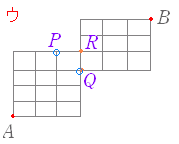
| (3) 次の図において,A 地点から B 地点まで遠回りせずに行くとき,途中,○印の地点は通り,×印の地点は通らない道順は何通りあるか. 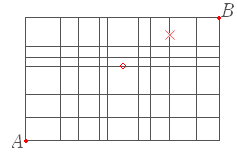 1. 64 通り |
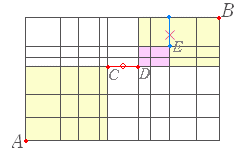 C 地点から D 地点は1通り. D 地点から B 地点へ×印を通らない道順は,(D→B 全体)−(×印を通る道順) = - ×1×1=35 - 6=29 通り 積の法則により,35×29=1015 通り(答) |
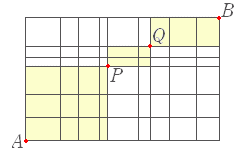
| (4) 次の図において,A 地点から B 地点まで遠回りせずに行く道順は何通りあるか. 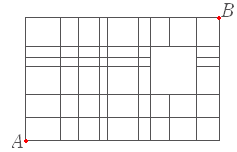 1. 1980 通り |
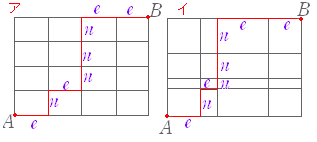
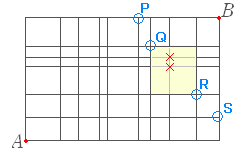 上図の,×印の箇所を通る道順を全体から引く.その際,n(少なくとも1つの×を通る)=n(下の×印を通る)+n(上の×印を通る)-n(両方の×印を通る)で数える. =1200 =1980 =720 ×印を通るのは 1200+1980 - 720=2460 通り - 2460=5005 - 2460=2545(答) (考え方1) 各道順が複数の関所を通らないように気をつけて関所を設置し,関所を通過する道順を加える. 上図の○印のように関所を設置すると,どの道も関所を重複して通ることはない. P を通る道順は,=462 通り Q を通る道順は,=1848 通り R を通る道順は,=225 通り S を通る道順は,=10 通り P または Q または R または S を通る道順は和の法則により,計 2545 通り(答) |
| (5) 次の図において,A 地点から B 地点まで遠回りせずに行く道順は何通りあるか. 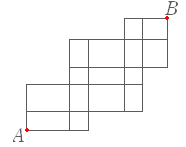 1. 180 通り |
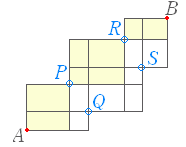 例えば,第1グループPの関所と第2グループRの関所を通る道順は,図の黄色の部分を通る.その道順は 同様にして,P,Sを通る道順は, 同様にして,Q,Rを通る道順は, 同様にして,Q,Sを通る道順は, 合計を和の法則で求めて,180 通り(答) |