|
■平方剰余
【例１】
（全体の見通し）･･･≪鉛筆遊びで戦う！≫a, b, cが正の整数のとき，a2+b2=c2ならば，a, bの少なくとも１つは3で割り切れることを示してください． ■3で割った余りの一覧表
しかし，どんな正の整数cをもってきても，c2を3で割った余りが2になることはない． 以上の内容を数学の答案風に作文すればよい． （解答） 正の整数cの２乗を3で割った余りは
(1) c=3kならばc2=9k2=3Nだから余り0
以上により，どんな正の整数cについても，その２乗を3で割った余りが2になることはない．…(A)(2) c=3k±1ならばc2=9k2±6k+1=3N+1だから余り1 ただし，k, Nは整数 一方，a, bの両方とも3で割り切れないとき
a, b=3m±1, 3n±1となるから，
となるからa2+b2を3で割った余りは2になる．…(B)a2+b2=3M+1+3N+1=3(M+N)+2 ただし，M, Nは整数 (A)(B)は矛盾だから，a2+b2=c2のとき，a, bの両方とも3で割り切れないことはない．すなわち，a, bの少なくとも１つは3で割り切れる．
【例２】
（全体の見通し）･･･≪鉛筆遊びで戦う！≫a, b, cが正の整数のとき，a2+b2=c2ならば，a, b, cの少なくとも１つは5で割り切れることを示してください． ■5で割った余りの一覧表
(1) 1+1 → 2となることはできない
以上の内容を，数学の答案風にまとめるとよい．(2) 1+4 → 0となることはできない (3) 4+4 → 3となることはできない （解答） (1) a=5m±1, b=5n±1のとき
a2+b2=5M+1+5N+1=5(M+N)+2となるが，どのようなc=5p±1, 5p±2を持ってきても
c2を5で割った余りは，1,4となり，余りが2となることはない．
(2) a=5m±1, b=5n±2またはa=5m±2, b=5n±1のとき
a2+b2=5M+4+5N+1=5(M+N+1)となるが，どのようなc=5p±1, 5p±2を持ってきても
c2を5で割った余りは，1,4となり，余りが0となることはない．
(3) a=5m±2, b=5n±2のとき
a2+b2=5M+4+5N+4=5(M+N+1)+3となるが，どのようなc=5p±1, 5p±2を持ってきても
c2を5で割った余りは，1,4となり，余りが3となることはない．
以上により，a, b, cとも5で割り切れない場合は，a2+b2=c2にならない．
【例３】
（全体の見通し）･･･≪鉛筆遊びで戦う！≫a, b, cが正の整数のとき，a2+b2=c2ならば，a, b, cの少なくとも１つは4で割り切れることを示してください． ■4で割った余りの一覧表
0+0=0 → あり得る
これでは，すべて4で割り切れないとき，4で割った余りが等しくならないと言い切れない．0+1=1 → あり得る 1+1=2 → あり得ない そこで，”解像度”（数学用語ではない．俗な言い方!!）を上げて8で割った余りで分類すると，次のようになる． ■8で割った余りの一覧表
1+1=2 → あり得ない
そこで，8で割った余りで分類して，答案をまとめるとよい．
（解答）1+4=5 → あり得ない 4+4=8→0 → あり得ない a, b, cとも4で割り切れないとき，
(1) a, bとも8で割った余りが1,3,5,7のいずれかであるとき，a2+b2=8M+1+8N+1=8(M+N)+2 → c2=8L+2は，あり得ない
以上により，a2+b2=c2が成り立つときに，a, b, cとも4で割り切れないと矛盾を生ずるから，a,b,cのうち少なくとも一つは4で割り切れる．
(2) a, bの一方は8で割った余りが1,3,5,7のいずれか，他方は2,6のいずれかであるとき，a2+b2=8M+1+8N+4=8(M+N)+5 → c2=8L+5は，あり得ない (3) a, bとも8で割った余りが2,6のいずれかであるとき，a2+b2=8M+4+8N+4=8(M+N+1) → c2=8Lは，あり得ない
【例４】
（全体の見通し）･･･≪鉛筆遊びで戦う！≫自然数a, b, cについて，等式a2+b2=c2が成り立ち，かつa, bは互いに素とする．このとき，次のことを証明せよ．
(1) aが奇数ならば，bは偶数であり，したがってcは奇数である．
(2) aが奇数のとき，a+c=2d 2となる自然数dが存在する． （京都大学）
■2で割った余りの一覧表
上の表では1+1=2 → 0もあり得る（cが偶数ならば受けられる）ことになって矛盾を示せないので，”解像度”（数学用語ではない．俗な言い方!!）を上げて4で割った余りで分類すると，次のようになる． ■4で割った余りの一覧表
(1) aもbも奇数のとき，4で割った余りは（上の表により） 1+1=2 となって，どんな自然数cを持ってきてもc2を4で割った余りは2にならないから，矛盾． したがって，bは偶数 aが奇数，bが偶数のとき，a2+b2は奇数になるから，c2は奇数，したがってcは奇数になる． (2) （「a,bは互いに素」という条件をどう使うか，それが問題だ） a2=c2−b2=(c−b)(c+b) だから
c−b=p2
c+b=q2 （p, qは1，奇数の素数またはそれらの積で，互いに素）とおける．
152+82=172のような場合に152=172−82=9×25において
このときc−b=3 c+b=3×25 のように分けると b==3×12, a=3×5 となって，「a,bは互いに素」という仮定に反する． c=, a=pq
だからa+c= =
ここで，p, qは奇数だから，p+q=2dとおける．a+c= = =2d 2
【問題５】
【例４】に次の小問を追加した場合，すなわち 自然数a, b, cについて，等式a2+b2=c2が成り立ち，かつa, bは互いに素とする． (3) aが奇数のとき，次のうちでつねに成り立つものを選んでください． （筆者が練習問題として追加したもの）
1b+c=k2となる自然数kが存在する 2b+c=2k2となる自然数kが存在する 3b+c=3k2となる自然数kが存在する 4b+c=4k2となる自然数kが存在する 5b+c=5k2となる自然数kが存在する HELP
【例４】の結果から，b+c=q2が成り立ちます．
他の選択肢が間違いであることは，１つの反例で示すことができます． すなわち，32+42=52の場合を考えると
b+c=9 → 2k2にならない
b+c=9 → 3k2にならない b+c=9 → 4k2にならない b+c=9 → 5k2にならない
→1
（参考１）
aは奇数，bは偶数，cは奇数として，a2+b2=c2が成り立ち，かつa, bは互いに素となる例
（参考２） 上記の【例４】においてp+q=2m, q−p=2nとおくと
a=m2−n2
となるからb==2mn c==m2+n2 a2+b2=c2（ピタゴラス数）で（aが奇数），a,bが互いに素な自然数の組はすべて， (m2−n2)2+(2mn)2=(m2+n2)2 の形に書くことができ， a+c=m2−n2+m2+n2=2m2 b+c=2mn+m2+n2=(m+n)2 が成り立ちます． |
［ポイント１］==ド・モルガンの法則==
（少なくとも１つは ･･･である）の否定は（すべて･･･でない）
［ポイント２］==背理法==
「ある命題が成り立つ」ことを示すには「その否定から矛盾を示せばよい」 【例１】では，「両方とも３で割り切れない」と仮定すれば矛盾を生ずるという構造になっています． （参考：前提の働き） ○ P:「a, b, cは正の整数」，Q:「a2+b2=c2」，R:「a, bの少なくとも１つは3で割り切れる」とするとき，もとの命題が
（PかつQ）ならばR
であるとき，これを対偶を用いて証明するには
ならば（または）
を示す必要があります．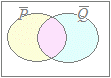
ならば（Pかつ）ならば（かつQ） ならば（かつ） の３通り考えられます． ○ これに対して，
PのときQならばR
の形の主張では，Pは前提といわれ，これが成り立たない場合を考える必要はありません． だから「PのときQならばR」の 「逆」を示したいときは
（PかつR）ならばQ
「裏」を示したいときは
（Pかつ）ならば
「対偶」を示したいときは
（Pかつ）ならば
を示せばよく，Pは常に仮定の側に入れてよいことになります．○ 特に，「PのときQならばR」を背理法で示すには，その否定
PかつQかつ → 矛盾
を示せばよいことになります．
【問題１】
a, b, cが正の整数で，a2+b2=c2のとき，次のうちでつねに成り立つものを選んでください． 1a, b, cのうち少なくとも1つは奇数 2a, b, cはすべて奇数 3a, b, cのうち少なくとも1つは偶数 4a, b, cはすべて偶数 HELP
（全体の見通し）
2で割った余りの一覧表
他方で，32+42=52 → 62+82=102のように，全部偶数という場合はあります．（1はダメ） 32+42=52の場合を考えると，全部偶数とは限りません．（4はダメ） → 2の否定が3なので，2が成り立たないことを証明すればよい． （記述問題のとき） a=2l+1, b=2m+1, c=2n+1のとき，
a2+b2=4L+1+4M+1=2(2L+2M+1)
となって，これらは等しくならないから，すべて奇数の場合は，a2+b2=c2とはならない．したがって，少なくとも１つは偶数．
c2=4N+1+=2(2N)+1
→3
【問題２】
a, b, c, dが正の整数で，a2+b2+c2=d 2のとき，次のうちでつねに成り立つものを選んでください． 1a, b, c, dのうち少なくとも1つは３の倍数 2a, b, c, dはすべて３の倍数 3a, b, c, dのうち少なくとも1つは３の倍数でない 4a, b, c, dはすべて３の倍数でない HELP
（全体の見通し）
3で割った余りの一覧表
12+22+22=32
なども参考にしながら，上の一覧表を見ると32+62+62=92 32+42+122=132 すべて３の倍数でなければ，3で割った余りは1+1+1=3 → 0となって，成り立たない．（4はダメ） 他方で，12+22+22=32 → 32+62+62=92のように，全部３の倍数という場合はあります．（3はダメ） 12+22+22=32の場合を考えると，全部３の倍数とは限りません．（2はダメ） → 4の否定が1なので，4が成り立たないことを証明すればよい． （記述問題のとき） a=3p±1, b=3q±1, c=3r±1, d=3s±1のとき，
a2+b2+c2=3P+1+3Q+1+3R+1=3(P+Q+R+1)
となって，これらは等しくならないから，すべて３の倍数でない場合は，a2+b2+c2=d 2とはならない．したがって，少なくとも１つは３の倍数．
d 2=3S+1
→1
【問題３】
nを正の整数とするとき，n2を6, 7 ,8, 9で割ったときの余りについて，正しいものを選んでください． 1余りが2になることはない 2余りが3になることはない 3余りが4になることはない 4余りが5になることはない HELP （全体の見通し）
余りが2,3,4になることは，反例として１つ示せばよい． 余りが5にならないことは証明すればよい．
→4
（記述問題のときの答案）n=3のときn2=9を7で割った余りは2になるから1は不可 n=3のときn2=9を6で割った余りは3になるから2は不可 n=4のときn2=16を6で割った余りは4になるから3は不可 n=6k,6k±1,6k±2,6k+3のときn2=6N, 6N+1, 6N+4, 6N+3だから6で割った余りは5にならない n=7k,7k±1,7k±2,7k±3のときn2=7N, 7N+1, 7N+4, 7N+2だから7で割った余りは5にならない n=8k,8k±1,8k±2,8k±3, 8k+4のときn2=8N, 8N+1, 8N+4, 8N+1, 8Nだから8で割った余りは5にならない n=9k,9k±1,9k±2,9k±3, 9k±4のときn2=9N, 9N+1, 9N+4, 9N, 9N+7だから9で割った余りは5にならない
【問題４】
a, b, cが正の整数で，a2+b2=c2のとき，次のうちでつねに成り立つものを選んでください． 1abは15の倍数になる 2abは24の倍数になる 3abcは48の倍数になる 4abcは60の倍数になる HELP
（全体の見通し）
【例題１，２，３】の結果から，a, b, cの少なくとも１つは3, 4, 5の倍数で，これらの３数は互いに素だからabcは3×4×5=60で割り切れます． 成り立たないことの証明は，反例を１つ示せばよい．
以下は，a, b, c≦50での例
(*) の場合abは15の倍数でない字下げは単なる定数倍 32+42=52 …(*) 62+82=102 92+122=152 …… 52+122=132 102+242=262 152+362=392 …… 72+242=252 142+482=502 …… 82+152=172 162+302=342 92+402=412 …… 122+352=372 …… 202+212=292 …… (*) の場合abは24の倍数でない (*) の場合abcは48の倍数でない
１個の例だけで全部答えられるので，他の例は証明上は不要．
→4
|