|
■共通部分が存在する条件
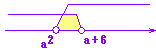
■ xの不等式「x>a かつ x<b」 が実数解をもつようなa,bの満たす条件は、a<b です。 |
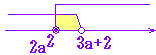
■ xの不等式「x≧a かつ x<b」が実数解をもつようなa,bの満たす条件は、 a<b です。
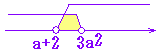
※ a=b のときは、共通部分がありません。 ■ xの不等式「x≧a かつ x≦b」が実数解をもつようなa,bの満たす条件は、 a≦b です。
|
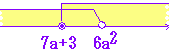
| ■ xの不等式「x>a または x<b」 の解が全実数となるようなa,bの満たす条件は、a<b です。
|
■ xの不等式「x≧a または x<b」 の解が全実数となるようなa,bの満たす条件は、a≦b です。
※ a=b のとき2つの範囲はつながります。 ■ xの不等式「x≧a または x≦b」 の解が全実数となるようなa,bの満たす条件は、a≦b です。
|