← PC用は別頁
|
【要点】
・中間項が消えれば和が求まります。 ・中間項が等比数列などになっても和が求まります。 ○等比数列の和
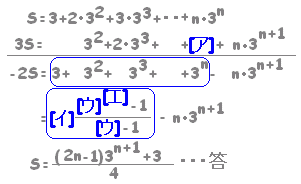
(1) 求める和をＳとおく。
(2) 公比ｒをかけてｒＳを作る。 (3) Ｓ－ｒＳを求めると，中間項が消えて，Ｓが求まる。 
 S(1−r)=a-arn となるから 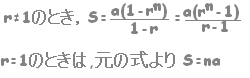 ○等差数列と等比数列の積になっている数列の和
「等差数列と等比数列の積になっている数列」とは，例えば次のようなものをいいます．
【例１】 初項１，交差１の等差数列an=nと初項１，公比２の等比数列bn=2n−1の積 anbn=n×2n−1 初めの幾つかを書くと 1, 2×21, 3×22,..., r×2r−1,..., n×2n−1 【例２】 初項3，交差2の等差数列an=2n+1と初項3，公比3の等比数列bn=3nの積 anbn=(2n+1)3n 初めの幾つかを書くと 3×31, 5×32, 7×33,..., (2r+1)3r,..., (2n+1)3n 等比数列の場合，S-rS により「中間項が消えるので」和が求まります． 等差×等比型の場合，結果を覚える形にすることはできませんが，上で示した方法を真似すると 「中間項が消えなくても」「中間項の和が求まるので」全体の和が求まります。 この場合は，「中間項が等比数列」となり，和が求まることになります。
【要点】
S−rSを作る ○Sが等比数列の和ならば ⇒ 「中間項が消えて」和が求まる． ○Sが等差数列×等比数列の和ならば ⇒ 「中間項が等比数列になって」和が求まる． |
|
【例1】 次の和を求めなさい。ただし，r≠1とする。
（答案）S=1+2r+3r2+4r3+5r4+・・・+nrn−1とおく −)rS=r+2r2+3r3+4r4+・・・+(n-1)rn−1+nrn S−rS=(r0+r1+r2+r3+r4+・・・+rn−1)−nrn ()内は等比数列の和になるので公式で和が求まります。 ()内は初項１，公比等比r，項数n（r1からrn−1まででｎ−1項，これに1=r0の項を付け加えるとｎ項）の等差数列の和数列の和だから 結局，求めるものは
（ビックリ答案から学ぼう）
※次の数列は等比数列ではありません： S=1+2r+3r2+4r3+5r4+・・・+nrn−1 今までに出会った間違い答案で，「どうしても合わない」という人は，この数列の公比を と考えていた例がありました。公比は”公”なのでｎによらない共通な定数でなければなりませんが，この数列には公比はありません！ どうしても納得しない方は， 1，3，5，7，… ，(2n−3)，(2n−1) という数列［公差2の等差数列］の公比が とは言えないことを思い出しましょう．
（参考）
wxMaxima（←インストール方法など）を使って，検算する方法 メニューから：微積分→数列の総和→
［関数］k*r^(k-1)
これにより，次の形で出力されます．［変数］k ［下端］1 ［上端］n ［数式で出力］にチェックを入れる
【例2】 次の和を求めなさい。ただし，x≠1とする。
（答案）S=2x+3x2+4x3+5x4+・・・+(n+1)xnとおく −)xS=2x2+3x3+4x4+・・・+nxn+(n+1)xn+1 S−xS=2x+(x2+x3+x4+・・・+xn)−(n+1)xn+1 ()内は等比数列の和になるので公式で和が求まります。 ()内は初項x2，公比等比x，項数n−1の等差数列の和数列の和だから 結局，求めるものは
（参考）
wxMaximaを使って，検算する方法 メニューから：微積分→数列の総和→
［関数］(k+1)*x^k
これにより，次の形で出力されます．［変数］k ［下端］1 ［上端］n ［数式で出力］にチェックを入れる |
|
■問題
１ 次の和を求めなさい。ただし，ｘ≠1とする。
(答案)
 |
||||||||||||
(正しいものを選びなさい。)
|
|
■問題
２ 次の和を求めなさい。
(答案)
  |
||||||||||||
(正しいものを選びなさい。)
|
 ...（携帯版）メニューに戻る...メニューに戻る
|
| 鬯ｮ�ｫ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ鬯ｮ�ｦ�ｽ�ｮ髯ｷ�ｻ�ｽ�ｻ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ鬯ｩ蟷｢�ｽ�｢�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｵ鬯ｩ蟷｢�ｽ�｢�ｽ�ｽ�ｽ�ｧ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�､鬯ｩ蟷｢�ｽ�｢髫ｴ荵暦ｿｽ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�･�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ鬯ｩ謳ｾ�ｽ�ｵ�ｽ�ｽ�ｽ�ｺ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｮGoogle鬯ｮ�ｫ�ｽ�ｶ�ｽ縺､ﾂ鬮ｫ�ｲ陝ｷ�｢�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�｢鬯ｮ�ｫ�ｽ�ｨ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ�ｽ�ｽ |
