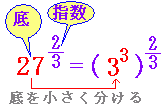
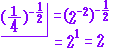問題2で分数の指数を伴った単項式の割り算が入るとき、割り算を先に掛け算に変換するという解法はないのでしょうか? ヒントでは係数ごとに指数法則で指数の加法法則でまとめるときにマイナスを掛けてから加法していますが、マイナスを掛けるというのもなぜそうするのか今一つ呑み込めません。
また、各単項式を2と3などの素数の積の形にした後に素数単位ごとに指数の加法法則が成り立つのも今ひとつよくわかりません。剰余算の記号が式に入っているからそう思ってしまうのかもしれませんが、剰余記号を省略して長い一つの単項式と理解すればよいのでしょうか?
=>[作者]:連絡ありがとう.質問が長いので区切って答えましょう.
(1)「割り算を先に掛け算に変換するという解法はないのでしょうか?」⇒一番初めの解説にありますように,

ですので,これは

と同じことです.つまり,割り算を掛け算に変換しています.
(2) 「マイナスを掛けるというのもなぜそうするのか今一つ」⇒負の指数の定義
この頁や
この頁の内容を先に読んでください.
(3) 「剰余算の記号が式に入っているから」⇒割り算の余りは使っていないので,この文章はおかしい.
(4) 「長い一つの単項式と理解すれば」⇒当然そうなっています.
(5) 「各単項式を2と3などの素数の積の形にした後に素数単位ごとに指数の加法法則が成り立つのも今ひとつよくわかりません」⇒たとえば,

のような場合,6と2に分けて(3まで分解せずに)済ませることもできますが,ほとんどの問題は素因数分解で行うのが最短・最良の解き方ですから,慣れるまで練習した方がよいでしょう.
※質問者がどういう現状で,何を尋ねているのか分かりにくいですが,推定で言えば「マイナスの指数がよく分からないから,使いたくない.逃げたい」という心理があると推定すれば,これらすべての質問がなぜ出てくるのかを説明できるようです.「マイナスの指数から逃げることはできません」ので上記2つの頁の「負の指数の定義」を読むことから始めてください.
いつもありがとうございます。
問題3の答え「4√a」と対になる問いに関して、いくら解こうとしても4√aになりません。ヒントを開けてみたところ、√3√a2乗bの解き方に誤りがあるような気がしていますが、いかがでしょうか?
=>[作者]:連絡ありがとう.点検しましたが,特に間違いはありませんでした.
累乗根の形で書く場合に,書いている人と読んでいる人が違う解釈をするかもしれないと思うものとして,次のような例があります.

と

の違い.

と

の違い.
以上は,通俗的に言えば,「肩」と「手のひら」が近くにある,「body」と「肩」が近くにあるための混同で,これらが紛らわしいときは横のスペースを適当に広げて書くと防ぐことはできます.
どちらかと言えば,あなたの疑問はその部分ではなく,次の「指数法則」が十分使えていないためではないでしょうか.
^{\frac{1}{3}})^{\frac{1}{2}}=(a^{\frac{2}{3}}b^{\frac{1}{3}})^{\frac{1}{2}}=a^{\frac{1}{3}}b^{\frac{1}{6}})
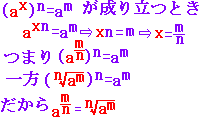
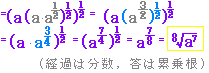
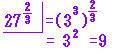 (2)
(2) 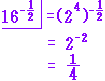 (3)
(3)