|
○ 高校の教科書程度の対数計算では，以下に述べる「対数を数値に直す公式」が使える場面が多く登場します．
•真数が特別な値になっているときは，計算機や数表を使わなくても対数の値が求められます．
•一般の場合には，対数の値は計算機や数表がなければ求められません．
底がa>0, a≠1の条件を満たしているとき
≪例≫
log21=0 log31=0
(1)←（証明）
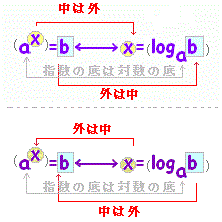ところで，どんなa>0, a≠1についてもa0=1 が成り立つから， loga1=0 になります．
≪例≫
log22=1 log33=1
(2)←（証明）
どんなa>0, a≠1についても a1=a が成り立つから， logaa=1 になります． |
※この頁に登場する基本的な問題は，社会生活で登場する実用的な計算と比較すると，「めったに登場しない特別な値」を扱っていることになります． 社会生活で登場する統計データについて対数の値を求めるには，この頁で述べる程度の基本が分かった上で，Excelなどを用いて計算します．Excelなどで求められる値は近似値です． ≪参考≫Excelの表計算関数 底がa，真数がxのときの対数の値 =log(x, a) ←数学での記号と順序が逆になっていることに注意
常用対数（底が10のときの対数）=log10(a) 自然対数（微分積分などを行うときに使う e=2.718...を底とする対数） =ln(a)
|
||||||||||||||||||||||||||||||||||||||
|
a>0, a≠1, M,N>0のとき
≪例≫
log102+log103=log10(2×3)=log106 log26+log27=log2(6×7)=log242
≪例≫
log512−log53=log5 =log54 log1050−log105=log10 =log1010=1 |
(3)←（証明）
(4)←（証明）
|
||||||||||||||||||||||||||||||||||||||
|
a>0, a≠1, M>0のとき
(logaM )nを表すときは（ ）を省略しません．． 
≪例≫
log102 3=3 log102（指数から係数へ） log35=log35 =log3（係数から指数へ） |
(5)←（証明）
|
||||||||||||||||||||||||||||||||||||||
問題次の値を求めてください．
log55において底（5）と真数（5）が同じだからlog55=1
|
log51において真数が1だから底（5）が何であってもlog51=0
|
|
log102+log105 =log10(2×5)=log1010と変形する． ここでlog1010=1 |
log412−log43 =log4(12÷3)=log44と変形する． ここでlog44=1 |
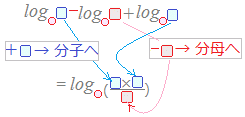log46−log430+log45=log4() =log41と変形する． ここでlog41=0 |
=log2()=log2 と変形する．
ここでlog2 =log22−2=−2log22=−2
|
|
log525=log552=2log55と変形する． ここでlog55=1だから，2log55=2 |
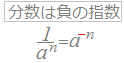log5=log5(5−2)=−2log55=−2と変形する． （別解）  log5=log51−log525=0−log552=−2 |
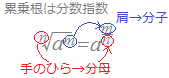log7 7=log7(7×7)=log77=log77=と変形する． |
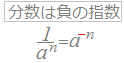log6 =log6(6−) =−log66=−と変形する． |
|
log10 +log10 =log10(×) =log10100 =log10102=2log1010=2 と変形する． |
log3 −3log3 =log3 −log3 ( )3
=log3 −log3 =log3( ×) =log3 =log33−1=−log33=−1 と変形する． |