|
■ 数学的帰納法とは(小話) ■ はじめに
[要点]
帰納法とは広く用いられている推論方法の一種で,特別な場合から一般の場合について推理するもので「その結果は,正しいことも間違っていることもある.」 これとは異なり,数学的帰納法による証明方法は常に正しい. ○ 広い意味での帰納法と演繹法 数学に限らず様々な場面で広く用いられる推論に「帰納法(きのうほう)」と「演繹法(えんえきほう)」がある. 帰納法というのは,「特殊から一般へ」向かう推論方法で,個々の具体的な事実から一般的な法則などを導き出す方法をいう. 帰納法の例
(1) 「○○県を旅行したとき,どの店でも親切にしてもらえた」ことから「○○県の人は親切だ」という結論を出す場合
のように,個々の幾つかの(ときには多数の)観察から適用範囲を広げて「すべての場合」について成り立つ命題を導き出す方法を帰納法という.(2) 「今日まで見たカラスは全部黒かった」ことから「すべてのカラスは黒い」という結論を出す場合 (3) 「晴れの日が3日続いた」ことから「これからも毎日晴れの日が続くだろう」と言う結論を出す場合 「帰納法から出される結論は,必ずしも正しいとは限らず正しいことも間違っていることもある」. 演繹法の例
(4) 日本国憲法では「すべて国民は,個人として尊重される」と定められていることから「あなたも個人として尊重される」という結論を出す場合
のように,一般的に成り立つ命題からある特定の命題を導き出す方法を演繹法という.(5) 「すべての正の整数は0よりも大きい」ことから「3は0よりも大きい」という結論を出す場合 元の命題が正しい限り「演繹法で導き出された結論はつねに正しい」. |
○ 広い意味での「帰納法」は必ずしも正しいとは限らない(正しいことも間違っていることもある).例えば左の(1)~(3)の例で考えると,「数個の」あるいは「多数の」観察しか行っていないのに「すべての」場合について結論を出そうとしているところに無理がある. 左の(3)の例では,3日しか観察しておらず,天候が分からない4日,5日,・・・についても「晴れ」と結論を出す所に無理がある.仮に,非常にまじめな子供がいて10日,100日,1000日(アフリカなどの砂漠で)観察して晴れであったとしても,この方法(帰納法)から結論を出そうとする限り根本的に無理であることが分かる.なぜなら,観察していない日が幾らでもあるからである. 左の(1)の例では○○県の「すべての人」の性格を調べることはおそらく無理.(2)については,いわゆるカラスについてはほとんど正しいと思われるが,佐賀県には豊臣秀吉が朝鮮出兵のときに連れ帰ったといわれるカササギというカラスの仲間がいて胴が白い・・・つまり黒くない. これに対して,左の例(4)では「すべての国民は・・・」といったときに「あなた」も含まれており,「あなた」というのはその一部分を取り出して見せているだけとなっている.実は「あなた」だけでなく,「わたし」も,他の誰かさんAも他の誰かさんBも「個人として尊重される」.このように演繹法は「すでに正しいと認められている事柄の一部を取り出して見せているだけ」なので常に正しいことになる. 左の例(5)についても「すべての正の整数」について述べているときに,1,2,3,4,5,・・・が0よりも大きいことはすでに述べられているから,3が0よりも大きいことは元の命題で述べられている内容よりも新しいことは何も言っていない.むしろ元の命題よりも情報量が減っている. このように,演繹法が常に正しいのは,元の命題で述べられている内容よりも広く新しい内容を何も付け加えないことと関係がある. ○ 絶対に間違いたくなければ演繹法だけを使えばよいが,その代わりに新しいことは何も言えないことになる.知識を広げるためには帰納法も必要となるが,個別の観察ですべての場合を尽くすことができない以上間違うことはあり,十分な観察で精度を高めることができるだけである. |
|
○ 数学的帰納法に使う考え方
[要点]
数学的帰納法が分かるには,重要なポイントが2つある. 数学的帰納法のイメージをつかむには「将棋倒しの論理」が分かりやすい. 実際の証明を行うには「仮定と結論 」の推論の仕方に慣れる必要がある. 数学的帰納法も見かけ上は「個別の観察から,すべての場合について結論を出す」形をしているので「数学的帰納法」と呼ばれるが,こちらの方は正確な証明方法となっている.次の例で,広い意味での帰納法と数学的帰納法の違いを示す. 例
すべての自然数 n について
1+3+5+ … +(2n - 1)=n2 …(1) が成り立つことを証明したい. [間違った証明]
n=1 のとき 1=n2 が成り立つ
n=2 のとき 1+3=22 が成り立つ n=3 のとき 1+3+5=32 が成り立つ よって,どんな n についても 1+3+5+ … +(2n - 1)=n2 が成り立つ この証明では 3 までしか調べていない.n=4 , 5 , 6 , … の場合について何も証明されていないことが分かる. そこで,まじめな生徒なら 100 まで調べるかもしれないが,それでも 101 以上は根拠のない作り話になってしまう.仮に,10000まで,100000まで調べても「整数は無限にあり,全部を調べることはできない」ので,この方法では結局証明はできない.広く用いられている帰納法,あるいはここで失敗した方法は「単純な数え上げ」の方法をとっていることに特徴があり,整数が無限にあるのに1つずつ調べていく方法にそもそも無理がある. このやり方では幾らやってもすべての自然数について成立することはできない. ところが,「すべての・・・」について成り立つことが証明できるものがある.これを右の例で見てみよう. 右に続く→
|
→続き [将棋倒しの論理] 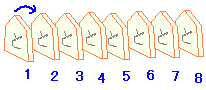 ドミノ倒し(将棋倒し)
ドミノ倒し(将棋倒し)(II) どの駒も「前の駒が倒れたら,自分も倒れる」ようにしておく. (I) 1番の駒は実際に手で倒す. 以上の方法により「すべての駒が倒れる」. (1つずつ手で倒しているのではないことに注意) このように,数学的帰納法は「将棋倒しの論理」のイメージだと考えるとよい.「将棋倒しの論理」に持ち込めば「すべて」についてどうなるか言える. [仮定と結論]
列車の行き先
「p ならば q 」という形の命題では,p の部分を仮定, q の部分を結論という.(II) 鉄道の列車は車両と次の車両とがしっかりつながれているので「ある車両が大阪に着けば,次の車両も大阪に着く」と言える. (I) 先頭の車両を実際に大阪駅まで到着させる. この場合「すべての車両は大阪駅に到着する」と言える. 上の例では「ある車両が大阪に着く」とは言っていないし,「次の車両も大阪に着く」とは言っていないことに注意.しっかり連結されているので「ある車両が大阪に着く」ことを仮定すれば「次の車両も大阪に着く」という関係だけを述べているところが重要. このような話は「仮定の話」「たら談義」などと呼ばれ, q を単独に約束するのではなく p の成立と連動させてあるところが鍵となっており,p 自体の成否,q 自体の成否は分からなくても「p ならば q 」は証明できる. 例 「すべての整数 n について,n>1 ならば n+1>2 」は正しい. なぜなら, n>1 の両辺に1を足すと n+1>2 が導けるから. この証明において,n>1 が成り立つとは言っていない.それは仮定しているだけ.また,n+1>2 も言っていない.それは,n>1 を仮定したときの結論となっている.それぞれが正しいかどうかは判断せずとも「これら2つの関係は証明できる」. |
|
[数学的帰納法による証明の例1]
すべての自然数 n について
※ n=1 のとき,左辺は 1+3+5+ … +1 にはならない.この式は 1 から順に 2n - 1 まで足すことを分かりやすく初めの2,3項を例として示したものなので, n=1 のときは +3+5 は付かない.(当然!!)1+3+5+ … +(2n - 1)=n2 …(1) が成り立つことを証明したい. ■正しい答案■ (I) n=1 のとき,左辺=1,右辺=12=1 だから,(1)は成り立つ. (II) n=k のとき,(1)が成り立つと仮定すると 1+3+5+ … +(2k - 1)=k2 …(2) (2)の両辺に 2k+1 を足すと 1+3+5+ … +(2k - 1)+(2k+1)=k2+2k+1=(k+1)2 …(3) (3)はn=k+1 のときも成立することを示している. (I)(II)より,すべての自然数 n について(1)が成り立つ. ※ n の式を証明するのになぜ k を使うのか : n=n のときとか,n=n+1 のときとか書くと,書き方がおかしく話がもつれてしまうので,他の文字を使ってすっきりさせる.n という変数がとる値が k という形をとる. 《上の答案はどこが悪いのか》 (I)について ▼ 1=1 が正しいのは小学生でも分かるが,それがこの問題の証明と何の関係があるのか示されていない. 「 n=1 のとき,左辺=1,右辺=12=1 だから,(1)は成り立つ.」と述べるべき. ▼ n=1 が成立しても意味がない.証明すべきことは n=1 のときに(1)式が成立するということなので,そう書かないといけない. 右に続く→
|
イラストによる解説 ・・・ (II)「前の電球が点灯すると,台車が動いて次の電球も点灯するようになっている」イルミネーションがあるとする.このとき,(I)「先頭の電球を点灯する」と全部の電球がつく
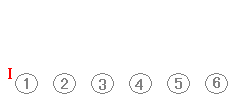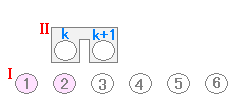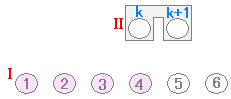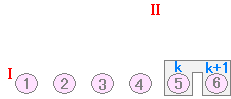 (I)で初めの電球だけは実際に点灯させなければならない. (II)で k の値は「変数」になっていて, k=1 のときは k+1=2 k=2 のときは k+1=3 k=3 のときは k+1=4 ・・・のように順に変化してすべての正の整数を表わせることが重要 →続き ▼ n=k のときと書いて,n に k を代入して,n=k+1 のときと書いて n に k+1 を代入しているので,n=k のときも n=k+1 のときも(1)が成立することを仮定しているだけになっている. 数学的帰納法の証明でもっとも重要なのは,上のイラスト図において「動く台車」の k と k+1 をつなぐ部分.左の証明では n=k のとき成立を仮定したのはよいとして, n=k+1 のときに成り立つことの証明がなされていない. 上の模範解答と下の零点答案との違いは =k2+2k+1= があるかないかだけに見えるが,この式がなければつながらない. n=k のときと n=k+1 のときをつなぐのが証明の核心なのにそれが書かれていないなければ証明とは言えない. ▼ 中には,n=k のときについても証明しようとする答案もときどきお目にかかるが,それもおかしい.n=k のときについても証明できるのなら数学的帰納法による証明はいらない. n=k のときについて(1)式を仮定して,n=k+1 のときについて(1)式が成り立つことを証明するという形にすべき. ▼ 「すべての自然数 n が成り立つ.」というのはおかしい.(1)式の証明をしているのだから「すべての自然数 n について(1)が成り立つ.」と書くべき. |
|
[数学的帰納法による証明の例2]
n が4以上の正の整数のとき,凸 n 角形の対角線の総数は
…(1) に等しいことを数学的帰納法で証明したい. (I) n=4 のとき,4角形の対角線は2本で,=2 だから(1)は成り立つ. (II) n=k (k≧4) のとき,(1)が成り立つと仮定すると 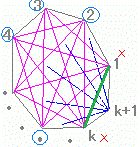
[青い線で示した]第k+1番目の頂点と2からk−1番目までの頂点を結んだk−2本と,[緑の線で示した]1とk番目を結ぶ,元は辺だったが新たに対角線になるものの合計1+(k−2)=k−1本
+k−1==== これは n=k+1 のときも成立することを示している. (I)(II)より,4以上のすべての自然数 n について(1)が成り立つ. |
※ 備考 この性質は4以上の正の整数 n について成立し,「すべての自然数 n について成立」するのではない.だから,第1段階は n=4 のときを示す. このように数学的帰納法による証明でも問題に応じて第1段階の n 値を考えなければならない. 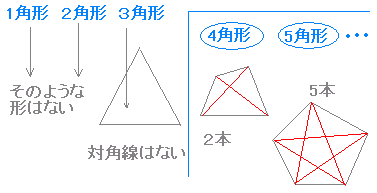 ※ n=k のときの結果を使って,n=k+1 のとき成立することを証明することが核心
【ⅠとⅡの関係】
通常の場合,数学の答案を分けて書くときは,「もれなく」「重複なく」分類します. 例えば ア)x<0のとき,… イ)x≧0のとき,… 例えば (1) nが奇数のとき,… (2) nが偶数のとき,… などと書き,これらの分類に「重複がある」ような答案は稚拙であって,めったに使いません. しかし,数学的帰納法の答案の(Ⅰ)(Ⅱ)の関係は,このような通常の数学の答案とは違います. ある関係式が「すべての自然数について成立する」ことを証明する場合
(Ⅰ) n=1のとき,その関係式が成り立つことを示す
この分類において(Ⅱ)のkの値は(Ⅰ)のn=1も含んでいなければなりません.(Ⅱ) n=kのとき,その関係式が成り立つと仮定すれば,n=k+1のときも成り立つことを示す たとえで言えば,(Ⅱ)でつながっている爆竹の端の値となっている(Ⅰ)に火をつけたら,次々と爆竹が発火していく仕組みなので,(Ⅱ)の値の中に(Ⅰ)の値が含まれていなければ,連鎖反応は起こりません. 凸n角形の対角線について証明した例で,「4以上のすべての自然数について成立する」ことを証明する場合
(Ⅰ) n=4のとき,その関係式が成り立つことを示す
のように,(Ⅱ)の端の値が(Ⅰ)になっているからこそ,「将棋倒しの仕組み」としての「数学的帰納法」の証明において端のスイッチが押せることになります.(Ⅱ) n=k (k≧4)のとき,その関係式が成り立つと仮定すれば,n=k+1のときも成り立つことを示す このように,数学的帰納法の証明では(Ⅰ)(Ⅱ)は重複のない分類ではなくて,(Ⅰ)は(Ⅱ)の端の値になっています. |